
- •III. Приложения определённого интеграла
- •§1. Площадь плоской фигуры
- •3. Условия квадрируемости фигур
- •4. Кривые с нулевой площадью
- •5. Свойства площади
- •6. Вычисление площади плоской фигуры
- •I. Вычисление площади плоской фигуры в декартовых координатах
- •II. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрическими уравнениями
- •III. Площадь в полярных координатах
- •§2. Кубируемые тела и их объёмы
- •1. Понятие кубируемого тела и его объема
- •2. Объём прямого цилиндрического тела
- •3. Вычисление объёма тела вращения
- •§3. Вычисление длины гладкой кривой
- •1. Понятие спрямляемой кривой и её длины
- •2. Вычисление длины гладкой кривой
- •§4. Площадь поверхности
6. Вычисление площади плоской фигуры
I. Вычисление площади плоской фигуры в декартовых координатах

1) Площадь криволинейной трапеции
Определение 1. Криволинейной трапецией называется фигура, ограниченная графиком функции y=f(x), где fC[a;b], a<b, f(x)≥0, x[a;b], прямыми x=a и x=b и отрезком [a;b] оси Ox.
Теорема 9. Криволинейная трапеция представляет собой квадрируемую фигуру F, площадь которой
 .
(13)
.
(13)
Доказательство.
![]() 1)
Криволинейная трапеция F
ограничена тремя отрезками и графиком
непрерывной функции f.
Тогда по теореме 5 F
– квадрируема.
1)
Криволинейная трапеция F
ограничена тремя отрезками и графиком
непрерывной функции f.
Тогда по теореме 5 F
– квадрируема.
2 )
Найдём(F).
)
Найдём(F).
Возьмём
![]() отрезка [a;b]
на частичные отрезки
отрезка [a;b]
на частичные отрезки
![]() ,
,![]() .
Обозначим через
.
Обозначим через![]() и
и![]() наименьшее и наибольшее значения функции
на
наименьшее и наибольшее значения функции
на![]() .
Составим суммы
.
Составим суммы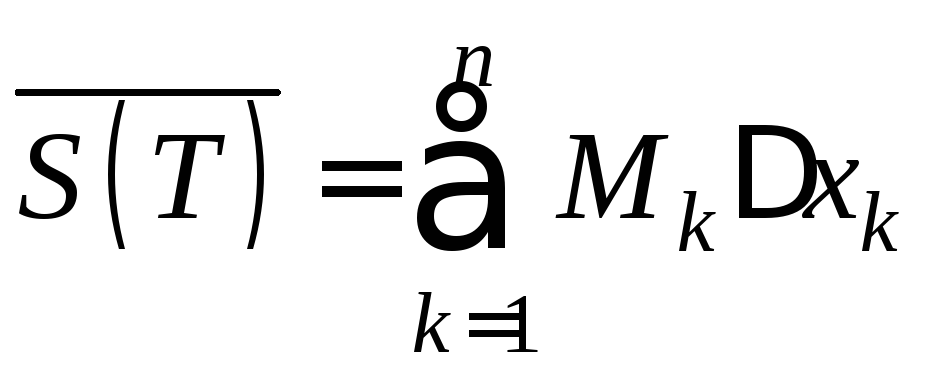 и
и .
Очевидно,
.
Очевидно,![]() и
и![]() - площади описанного и вписанного околоF
многоугольников. Следовательно,
- площади описанного и вписанного околоF
многоугольников. Следовательно,
![]() . (14)
. (14)
По
условию fC[a;b]
 .
.
Переходя
к пределу в (14), получим (13).
![]()
Геометрический смысл определенного интеграла.
О пределенный
интеграл
пределенный
интеграл
 равен
площади
криволинейной
трапеции, ограниченной графиком функции
y=f(x),
где fC[a;b],
a<b,
f(x)≥0,
x[a;b],
прямыми x=a
и x=b
и отрезком [a;b]
оси Ox.
равен
площади
криволинейной
трапеции, ограниченной графиком функции
y=f(x),
где fC[a;b],
a<b,
f(x)≥0,
x[a;b],
прямыми x=a
и x=b
и отрезком [a;b]
оси Ox.
2) Фигура F ограничена графиком функции y=f(x), где fC[a;b], a<b, f(x)≤0, x[a;b], прямыми x=a и x=b и отрезком [a;b] оси Ox.
![]() тоже
будем называть криволинейной трапецией.
Т. к. f(x)≤0,
то -f(x)≥0,
и, значит, к фигуре F1
можем применить формулу 1:
тоже
будем называть криволинейной трапецией.
Т. к. f(x)≤0,
то -f(x)≥0,
и, значит, к фигуре F1
можем применить формулу 1:
 .
.

 .
(15)
.
(15)
3)
![]() иf(x)
меняет знак в конечном числе точек
[a;b].
иf(x)
меняет знак в конечном числе точек
[a;b].
Разобьем фигуру F на части, в каждой из которых f(x) не меняет знак, и применим ответствующую формулу (13) или (15).
![]() ,
,
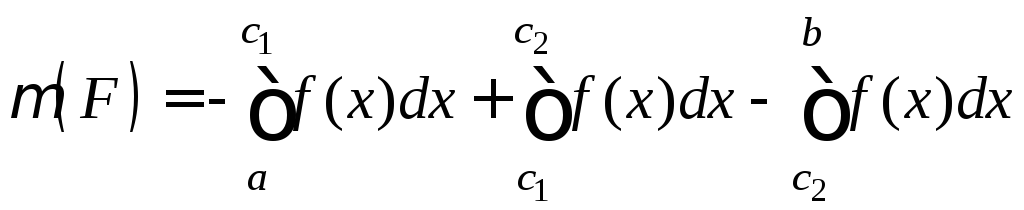 .
.
4 )
Фигура ограничена снизу графиком функцииy=f1(x),
сверху - y=f2(x),
)
Фигура ограничена снизу графиком функцииy=f1(x),
сверху - y=f2(x),
![]() ,
,![]() ,
и с боков прямымиx=a,
x=b.
,
и с боков прямымиx=a,
x=b.
F=F2\F1,
где F1
ограничена сверху графиком y=f1(x),
а F2
– графиком y=f2(x).
Так как
![]() ,
то
,
то
 .
.
По
свойству интеграла
 .
.
II. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрическими уравнениями
Теорема
10.
Пусть криволинейная трапеция
![]() ограничена кривойАВ,
заданной параметрическими уравнениями:
ограничена кривойАВ,
заданной параметрическими уравнениями:

![]() .
.
Е сли: 1)
сли: 1)![]() и
и![]() ,
,
2)
![]() и
и![]() ,
,
3)
![]() ,
,
то криволинейная трапеция квадрируема и справедлива формула:
 . (16)
. (16)
Доказательство.
![]() Так
как
Так
как
![]() ,
то существует обратная функция
,
то существует обратная функция![]() ,
возрастающая и непрерывная на [a;b].
Следовательно,
,
возрастающая и непрерывная на [a;b].
Следовательно,
![]() .Таким
образом, криваяАВ
является графиком функции y=f(x),
где
.Таким
образом, криваяАВ
является графиком функции y=f(x),
где
![]() .
Тогда по теореме 9 криволинейная трапеция
квадрируема и её площадь
.
Тогда по теореме 9 криволинейная трапеция
квадрируема и её площадь
 .
.
Выполним
здесь подстановку:
![]() .
.
![]() .
Т. о., получаем (16).
.
Т. о., получаем (16).
![]()
Формула
(16) справедлива и для случая
![]() .
.
Если
 (0tT)
– параметрические уравнения простой
замкнутой кривой, пробегаемой против
хода часовой стрелки и ограничивающей
слева
от себя фигуру F,
то
площадь
фигуры можно вычислить по одной из
формул:
(0tT)
– параметрические уравнения простой
замкнутой кривой, пробегаемой против
хода часовой стрелки и ограничивающей
слева
от себя фигуру F,
то
площадь
фигуры можно вычислить по одной из
формул:
 ,
,  ,
,
 . (17)
. (17)
П ример.Вычислить
площадь фигуры, ограниченной астроидой
ример.Вычислить
площадь фигуры, ограниченной астроидой
![]()

![]() .
.
Т. к. фигура F ограничена замкнутой линией, то удобно применить формулу (17).



 .
.
III. Площадь в полярных координатах
1) Пусть кривая L задана в полярной системе координат уравнением:
![]() .
.
О пределение.
Криволинейным
сектором
называется плоская фигура, ограниченная
кривой L
и двумя лучами, составляющими с полярной
осью углы
пределение.
Криволинейным
сектором
называется плоская фигура, ограниченная
кривой L
и двумя лучами, составляющими с полярной
осью углы
![]() .
.
Теорема 11. Криволинейный сектор представляет собой квадрируемую фигуру F, площадь которой вычисляется по формуле:
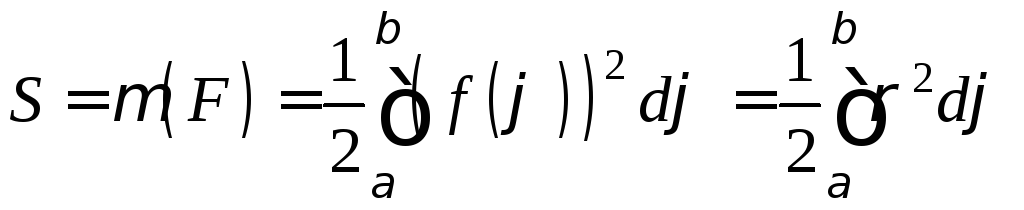 .
.
Доказательство.
![]() Выберем
произвольное разбиение отрезка
Выберем
произвольное разбиение отрезка
![]() точками
точками![]() наn
частей
наn
частей
![]() .
Проведём лучи
.
Проведём лучи![]() .
Сектор разбит наn
частей. Т.к.
.
Сектор разбит наn
частей. Т.к.
![]() ,
то на каждом из частичных отрезков
,
то на каждом из частичных отрезков![]() она имеет наибольшее
она имеет наибольшее![]() и наименьшее
и наименьшее![]() значения. На
значения. На![]() построим два круговых сектора с радиусами
построим два круговых сектора с радиусами![]() и
и![]() .
Получим две ступенчатые квадрируемые
фигуры. Одна из нихP
содержится в секторе, а другая Q
его содержит. Площади этих ступенчатых
фигур
.
Получим две ступенчатые квадрируемые
фигуры. Одна из нихP
содержится в секторе, а другая Q
его содержит. Площади этих ступенчатых
фигур
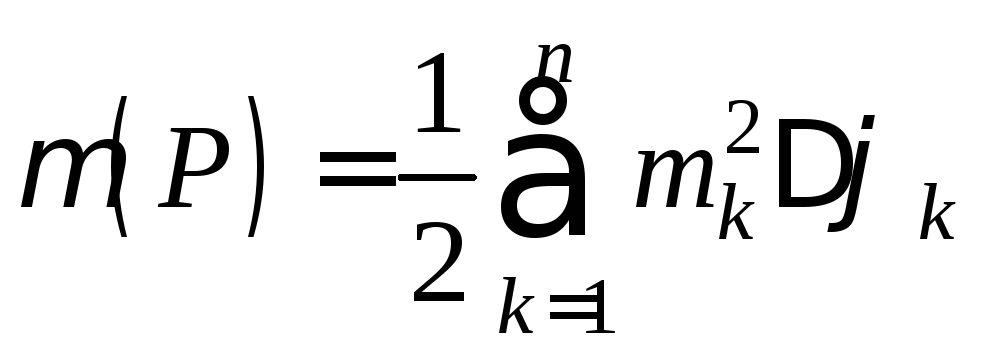 ,
,  ,
, ![]() .
.
![]() и
и
![]() - нижние и верхние интегральные суммы
для функции
- нижние и верхние интегральные суммы
для функции![]() ,
то есть
,
то есть![]() ,
,
![]() .
.
Так
как функция
![]() ,
то она интегрируема на
,
то она интегрируема на![]() ,
то есть
,
то есть![]() выполнено
выполнено![]() .
Пусть<.
Тогда по теореме 2 фигура F
квадрируема (так как
.
Пусть<.
Тогда по теореме 2 фигура F
квадрируема (так как
![]() нашлись две квадрируемые фигурыP
и Q,
нашлись две квадрируемые фигурыP
и Q,
![]() ,
такие, что
,
такие, что![]() ).
).
Так
как функция
![]() интегрируема на
интегрируема на![]() ,
то
,
то
 .
.
Так
как
![]() ,
то
,
то .
.![]()

2)
Пусть фигура ограничена кривыми
![]() ,
,![]() ,
,
![]() на
на
![]() и лучами=,
=.
Тогда
и лучами=,
=.
Тогда
 .
.
