
- •I. Числовые ряды
- •§1. Основные понятия
- •1. Понятие числового ряда. Сходящиеся и расходящиеся ряды
- •2. Остаток сходящегося ряда
- •3. Свойства сходящихся рядов
- •4. Необходимое условие сходимости ряда
- •§ 2. Положительные ряды
- •§3. Сходимость произвольных рядов (Критерий Коши сходимости числового ряда)
- •§4. Знакопеременные ряды
- •1. Абсолютная и условная сходимость
- •2. Свойства сходящихся рядов
- •3. Признаки абсолютной сходимости рядов
- •§5. Знакочередующиеся ряды
- •1. Признак Лейбница
- •2. Оценка остатка ряда Лейбница.
4. Необходимое условие сходимости ряда
Теорема 5. Если
ряд (1)
![]() сходится, то
сходится, то![]() .
.
Доказательство.
![]() Так как ряд (1)
сходится, то
Так как ряд (1)
сходится, то
![]() ,
,![]() .
.![]() выполнено
выполнено![]() .
Тогда
.
Тогда![]() .
.![]()
Заметим,
что обратное
утверждение неверно.
То есть из того, что
![]() не следует,
что ряд (1) сходится (необходимое условие
сходимости не является достаточным).
Примером служит ряд
не следует,
что ряд (1) сходится (необходимое условие
сходимости не является достаточным).
Примером служит ряд
![]() ,
который называетсяосновным
гармоническим рядом.
,
который называетсяосновным
гармоническим рядом.
(Как видно,
![]() -го
члена этого ряда равна нулю, но ряд
расходится).
-го
члена этого ряда равна нулю, но ряд
расходится).
Пример 5. Доказать
расходимость ряда
![]() .
.
Δ Допустим
противное:
ряд
![]() сходится.
сходится.
Рассмотрим
![]() ;
;
![]() .
.
Т. к. по предположению
ряд сходится, то
![]() и
и![]() .
Следовательно,
.
Следовательно,![]() .
.
Согласно определению
предела это означает, что
![]()
выполнено
![]() .
(
.
(![]() )
)
Но
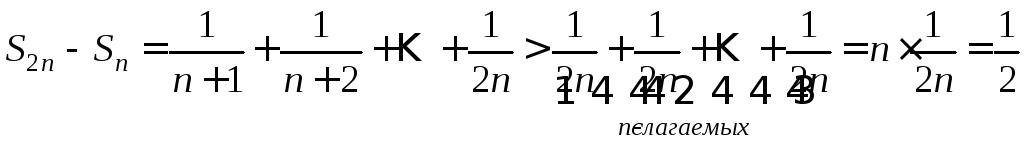 .
.
То
есть
![]() - противоречие с (
- противоречие с (![]() ),
которое показывает, что наше предположение
неверно. Значит, основной гармонический
ряд
),
которое показывает, что наше предположение
неверно. Значит, основной гармонический
ряд![]() расходится. Δ
расходится. Δ
Замечание. Из
теоремы 5 следует, что если
![]() (в том числе не существует), то рядрасходится.
(в том числе не существует), то рядрасходится.
Например,
![]() расходится, так как
расходится, так как![]() .
.
![]() расходится, так
как
расходится, так
как
![]() .
.
![]() расходится, так
как
расходится, так
как
![]()
 .
.
§ 2. Положительные ряды
![]()
Определение. Положительным рядом называется ряд, все члены которого неотрицательны.
(Правильнее было бы назвать такие ряды неотрицательными, но по традиции они называются положительными).
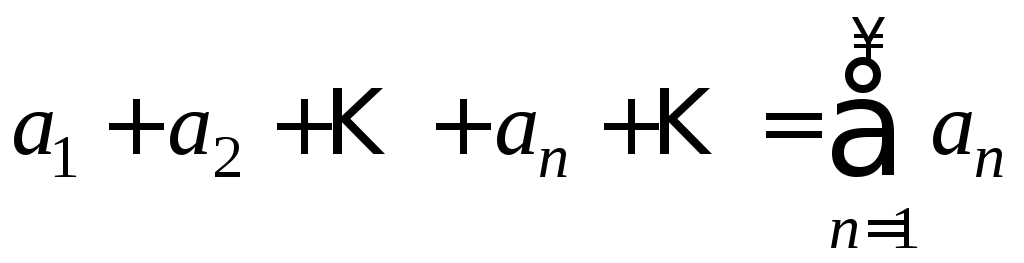 ,
где
,
где
![]() ,
,![]() (1)
(1)
Рассмотрим частичные суммы ряда (1):
S1=a1;
S2=a1+a2= S1+a2≥ S1;
S3=a1+a2+a3= S2+a3≥ S2;
……………..
Sn=a1+a2+…+ an-1 +an= Sn-1+ an≥ Sn-1 .
Последовательность
![]() неотрицательная, неубывающая. Напомним,
что имеет место следующее утверждение:
всякая неубывающая и ограниченная
сверху последовательность имеет предел.
неотрицательная, неубывающая. Напомним,
что имеет место следующее утверждение:
всякая неубывающая и ограниченная
сверху последовательность имеет предел.
Теорема 6. (необходимое и достаточное условие сходимости).
Для того, чтобы
ряд (1) сходился, необходимо и достаточно,
чтобы последовательность его частичных
сумм
![]() была ограничена сверху.
была ограничена сверху.
Доказательство.
![]() 1. Необходимость.
1. Необходимость.
Пусть ряд (1)
сходится. Тогда существует конечный
![]() Следовательно,
Следовательно,![]() ограничена и, значит, ограничена сверху
(так как последовательность неотрицательная
и неубывающая).
ограничена и, значит, ограничена сверху
(так как последовательность неотрицательная
и неубывающая).
2. Достаточность.
Пусть
![]() ограничена сверху. Так как
ограничена сверху. Так как![]() неубывающая, то она имеет предел,
следовательно, ряд (1) сходится.
неубывающая, то она имеет предел,
следовательно, ряд (1) сходится.![]()
Решить вопрос о
сходимости ряда с помощью теоремы 6
можно лишь в редких случаях (для
![]() уже сложно). Рассмотрим теоремы, которые
являются более удобными для практического
использования.
уже сложно). Рассмотрим теоремы, которые
являются более удобными для практического
использования.
Теорема 7 (общий
признак сравнения). Пусть даны два
положительных ряда
![]() (А) и
(А) и![]() (B)
и
(B)
и
![]() выполнено
выполнено![]() . (2)
. (2)
Тогда 1) если
![]() сходится, то
сходится, то![]() тоже сходится,
тоже сходится,
2) если
![]() расходится, то
расходится, то![]() тоже расходится.
тоже расходится.
Доказательство.
![]() Обозначим
Обозначим
![]() .
.
Из (2) следует
![]()
![]() .
.
1) Пусть ряд
![]() сходится. Тогда по теореме 6
сходится. Тогда по теореме 6![]() ограничена сверху. Следовательно,
ограничена сверху. Следовательно,![]() ограничена сверху. Значит, по теореме
6 ряд
ограничена сверху. Значит, по теореме
6 ряд![]() сходится.
сходится.
2) Пусть ряд
![]() расходится. Докажем, что и
расходится. Докажем, что и![]() расходится. Предположим противное:
расходится. Предположим противное:![]() сходится. Но тогда, по только что
доказанному, ряд
сходится. Но тогда, по только что
доказанному, ряд![]() сходится. Это противоречит условию.
Следовательно, наше предположение
неверно, и
сходится. Это противоречит условию.
Следовательно, наше предположение
неверно, и![]() расходится.
расходится.![]()
Замечание. Теорема
7 справедлива и в случае, когда неравенство
(2) выполнено не для любого
![]() ,
а, начиная с некоторого номера, то есть
,
а, начиная с некоторого номера, то есть![]() .
Справедливость этого заключения вытекает
из теоремы 1 о сходимости остатка ряда.
.
Справедливость этого заключения вытекает
из теоремы 1 о сходимости остатка ряда.
При исследовании рядов на сходимость с помощью признака сравнения мы должны иметь ряды, сходимость которых известна (с чем сравнивать).
!
![]() (геометрический ряд) сходится при
(геометрический ряд) сходится при![]()
расходится
при
![]() .
.
!
![]() (гармонический ряд) сходится при
(гармонический ряд) сходится при![]() ,
,
расходится
при
![]() .
.
(При
![]() - основной гармонический ряд.)
- основной гармонический ряд.)
Пример 1. Исследовать
на сходимость ряд
![]() .
.
Δ
![]() .
.
Ряд
![]() сходится, так как это геометрический
ряд с
сходится, так как это геометрический
ряд с![]() .
.
Следовательно, по теореме 7 данный ряд сходится. Δ
Пример 2. Исследовать
на сходимость ряд 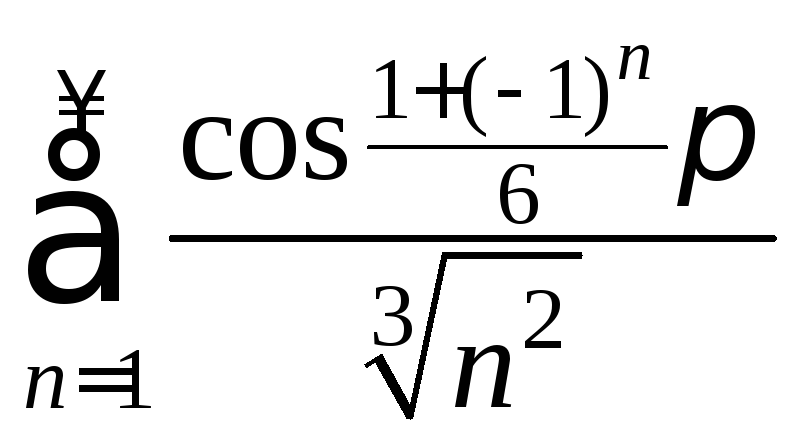 .
.
Δ

![]()
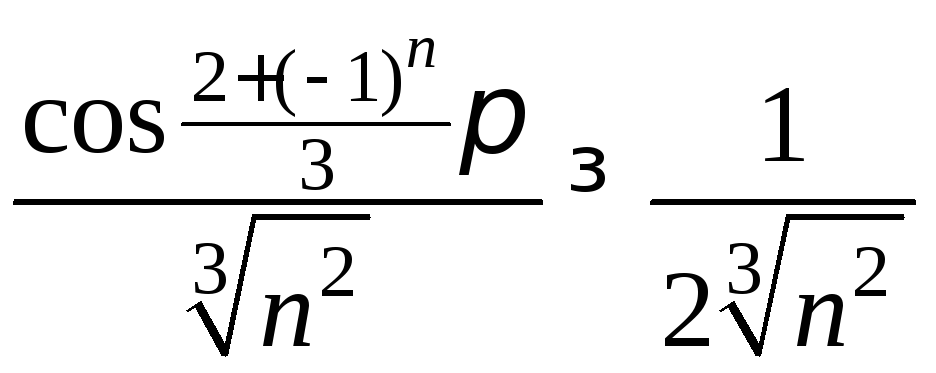 .
.
Ряд
![]() расходится (гармонический ряд,
расходится (гармонический ряд,![]() ),
следовательно, ряд
),
следовательно, ряд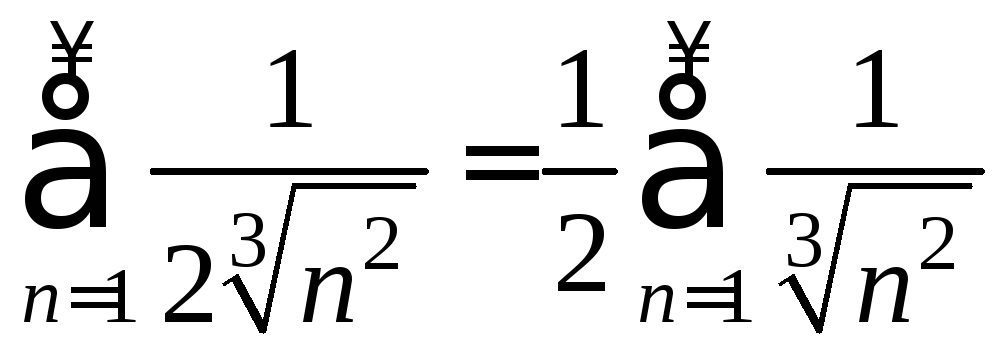 расходится. Тогда (по теореме 7) данный
ряд (ряд с большими членами) расходится.
Δ
расходится. Тогда (по теореме 7) данный
ряд (ряд с большими членами) расходится.
Δ
Теорема
8 (частный
признак сравнения). Пусть даны два
положительных ряда
![]() (А) и
(А) и![]() (В),
(В),![]()
![]() (ряд (В) – строго положительный) и
(ряд (В) – строго положительный) и
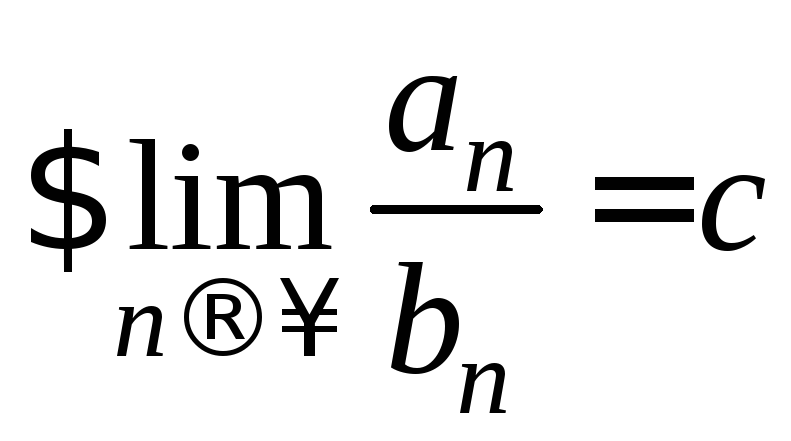
![]() .
.
Тогда: 1) если ряд
![]() сходится и
сходится и![]() ,
то ряд
,
то ряд
![]() сходится;
сходится;
2) если ряд
![]() расходится и
расходится и![]() ,
то
,
то
![]() расходится.
расходится.
Доказательство.
![]() По условию
По условию
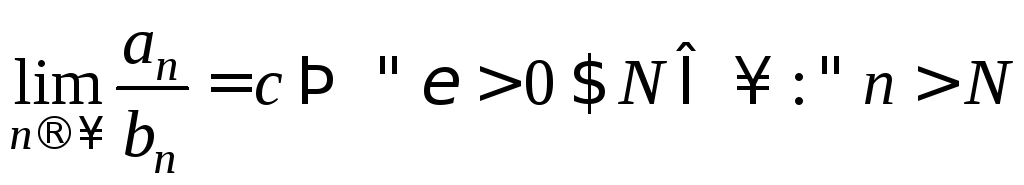 выполнено
выполнено![]() ,
т. е.
,
т. е.
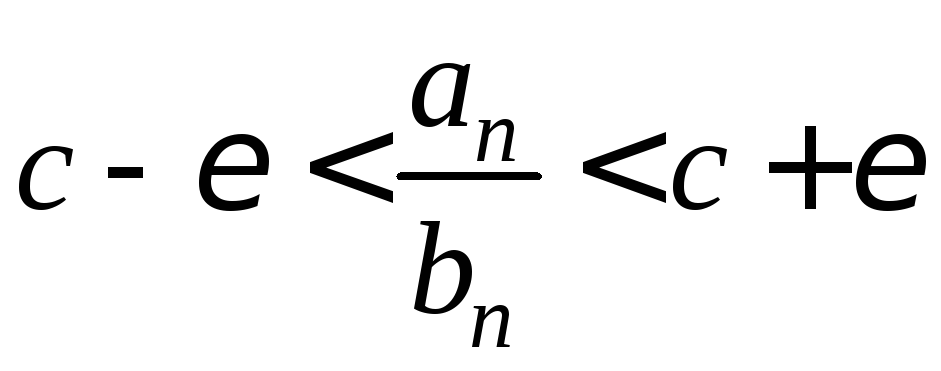 . (3)
. (3)
1) Пусть ряд
![]() сходится и
сходится и![]() .
Из (3)
.
Из (3)![]()
![]() .
.
Так как ряд
![]() сходится, то по теореме 4 сходится и ряд
сходится, то по теореме 4 сходится и ряд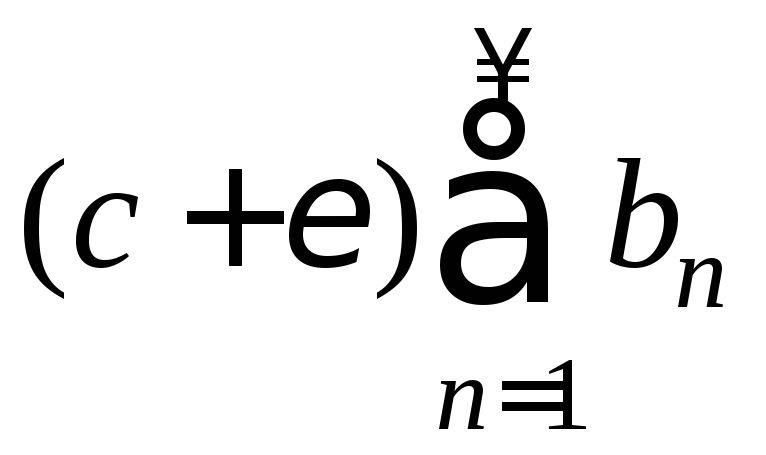 следовательно, (по т. 7 и замечанию)
сходится и ряд
следовательно, (по т. 7 и замечанию)
сходится и ряд
![]() .
.
2) Пусть ряд
![]() расходится,
расходится,![]() .
Из неравенства (3)
.
Из неравенства (3)
![]() .
.
Пусть
![]() - конечное число. Так как ряд
- конечное число. Так как ряд![]() расходится, то расходится и ряд
расходится, то расходится и ряд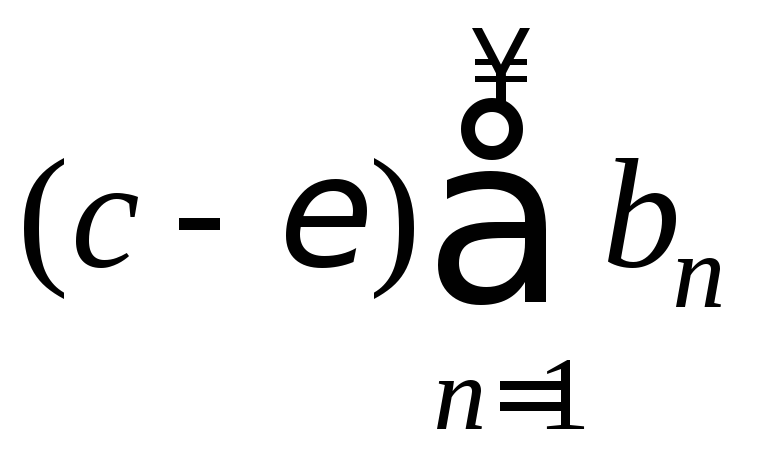 .
Следовательно, (по т. 7 и замечанию)
расходится и ряд
.
Следовательно, (по т. 7 и замечанию)
расходится и ряд
![]() .
.
Если
![]() ,
то из последнего неравенства получаем
,
то из последнего неравенства получаем![]() .
Следовательно, по необходимому условию
сходимости ряд
.
Следовательно, по необходимому условию
сходимости ряд
![]() расходится.
расходится.
Замечание.
Если
![]() ,
то ряды
,
то ряды
![]() и
и
![]() эквивалентны по сходимости (то есть
сходятся или расходятся одновременно).
эквивалентны по сходимости (то есть
сходятся или расходятся одновременно).
Пример 1. Исследовать
на сходимость ряд
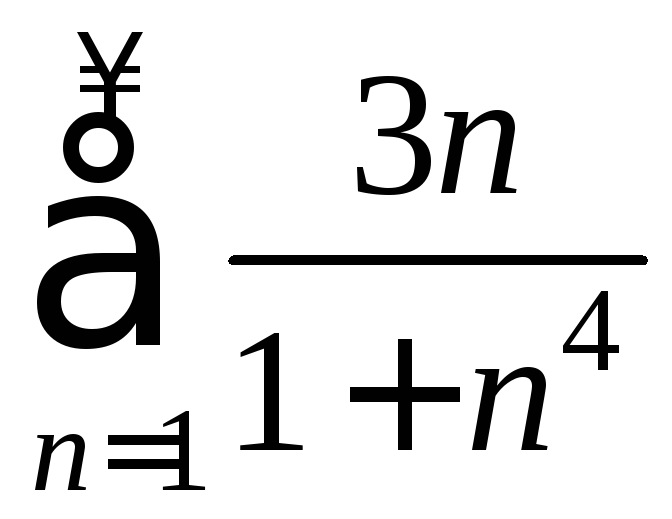 .
.
Δ
Сравним с
рядом
![]() ,
который сходится.
,
который сходится.
![]() .
.
Значит, (по
т. 8) ряд
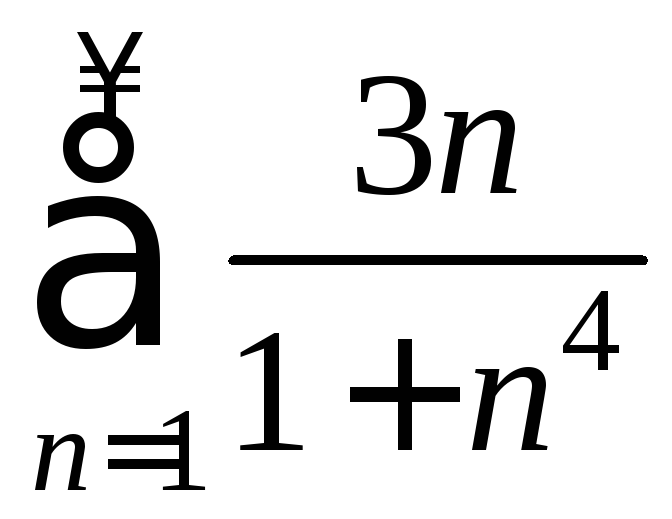 сходится. Δ
сходится. Δ
Пример 2. Исследовать
на сходимость ряд
![]() .
.
Δ Сравним с рядом
![]() - расходящийся.
- расходящийся.
 .
.
Следовательно, (по т. 8) ряды эквивалентны по сходимости, то есть данный ряд расходится. Δ
Теорема 9 (признак
Даламбера). Пусть дан ряд
![]() ,
,![]() (ряд строго положительный). Пусть
(ряд строго положительный). Пусть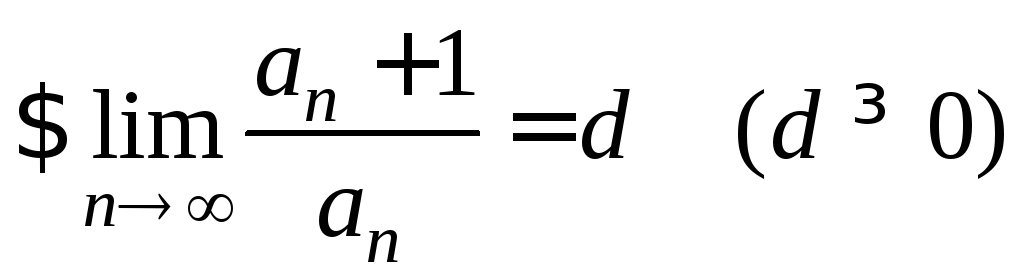 . (5)
. (5)
Тогда: 1) ряд сходится, если d<1 (в том числе и d=0);
2) ряд расходится, если d>1 (в том числе и d=+).
(В случае d=1 заключения о сходимости ряда сделать нельзя).
Доказательство.
![]() 1)
d<1.
1)
d<1.
Зафиксируем
![]() так, чтобыd+<1.
Обозначим d+=q,
q<1.
так, чтобыd+<1.
Обозначим d+=q,
q<1.
Из (5) следует, что
для выбранного
![]() выполнено
выполнено
 или
или
![]()
 .
.
Отсюда
![]()
То есть для ![]()
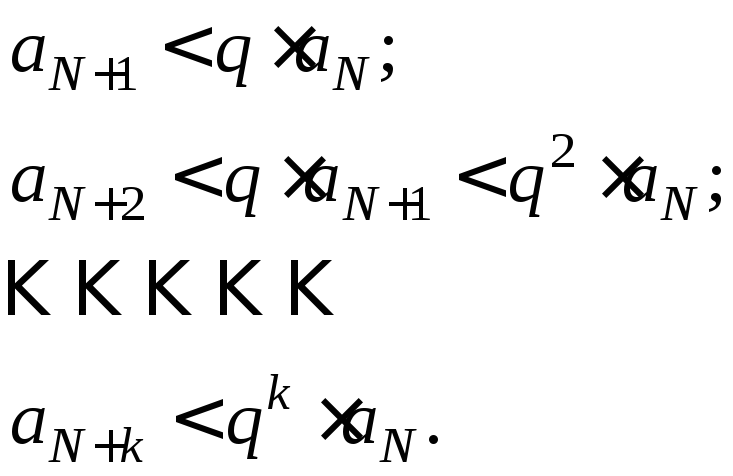 (6)
(6)
Рассмотрим ряды
![]() (7)
и
(7)
и![]() (8).
Ряд (8) сходится (геометрический ряд,
(8).
Ряд (8) сходится (геометрический ряд,![]() ).
В силу (6) члены ряда (7) не больше
соответствующих членов ряда (8).
Следовательно, (по т. 7) ряд (7) сходится.
Но ряд (7) – это остаток ряда
).
В силу (6) члены ряда (7) не больше
соответствующих членов ряда (8).
Следовательно, (по т. 7) ряд (7) сходится.
Но ряд (7) – это остаток ряда![]() следовательно, (по т. 1) ряд
следовательно, (по т. 1) ряд![]() сходится.
сходится.
2) d>1.
Зафиксируем
![]() .
.
Из (5) следует, что
для выбранного
![]() выполнено
выполнено
![]() .
.
Тогда
![]() и, следовательно, (по необходимому
условию сходимости) ряд
и, следовательно, (по необходимому
условию сходимости) ряд![]() расходится.
расходится.![]()
Заметим, что в случае d=1 ряд может как сходиться, так и расходиться.
Например,
![]() расходится,
расходится,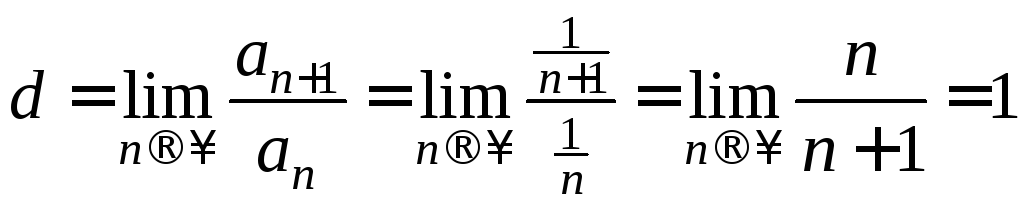 ,
,
а ряд
![]() сходится,
сходится,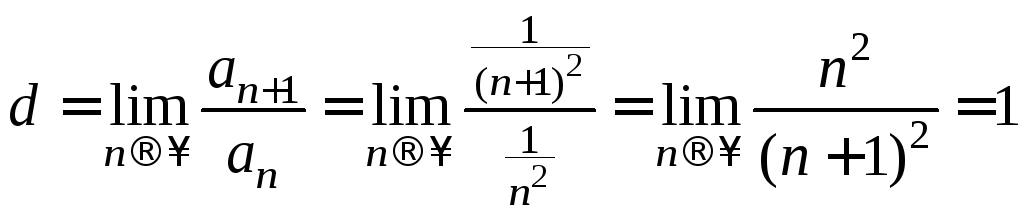 .
.
Пример.
![]()
Δ
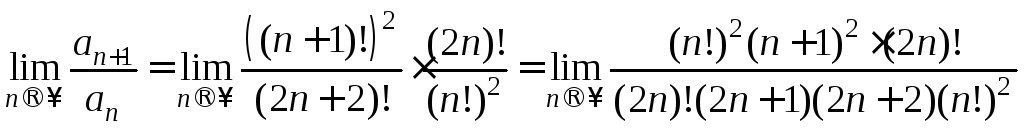 =
=
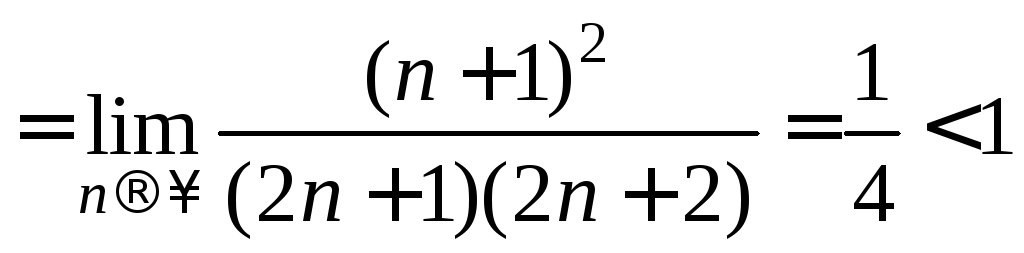 .
Следовательно, данный ряд сходится.
Δ
.
Следовательно, данный ряд сходится.
Δ
Теорема 10 (признак
Коши). Пусть дан положительный ряд
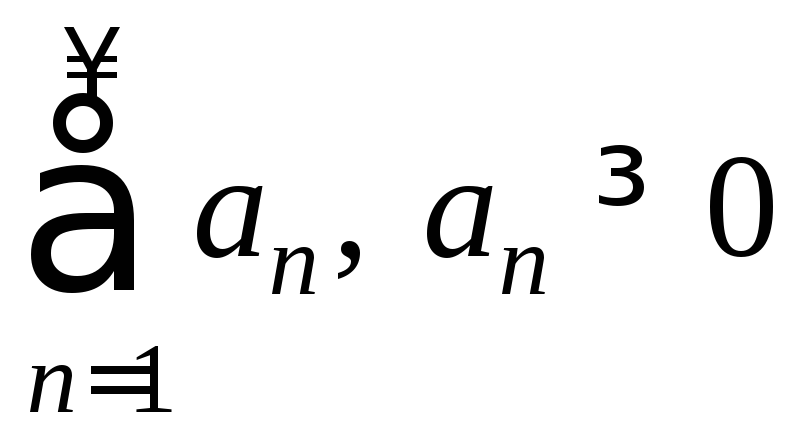
![]() ,
и
,
и![]() . (9)
. (9)
Тогда: 1) если k<1, то ряд сходится (в том числе k=0);
2) если k>1,
то ряд расходится (в том числе
![]() .
.
(В случае k=1 ряд может как сходиться, так и расходиться.)
Доказательство.
![]() 1)
k<1.
1)
k<1.
Зафиксируем
![]() .
Обозначим
.
Обозначим![]() .
.
Из (9) следует, что
для выбранного
![]() выполнено
выполнено
![]() или
или
![]() .
.
Отсюда
![]() .
То есть
.
То есть![]() . (10)
. (10)
Рассмотрим ряды
![]() (11) и
(11) и![]() (12). Ряд (12) сходится (геометрический ряд,
(12). Ряд (12) сходится (геометрический ряд,![]() ).
Тогда по общему признаку сравнения (т.
7) из (10) следует что
).
Тогда по общему признаку сравнения (т.
7) из (10) следует что![]() сходится. Следовательно, (по т. 1) сходится
и ряд
сходится. Следовательно, (по т. 1) сходится
и ряд![]() .
.
2) k>1.
Так как
![]() ,
то
,
то![]()
![]() .
Значит,
.
Значит,![]()
![]() .
Поэтому
.
Поэтому![]() .
Следовательно, по необходимому условию
сходимости, ряд (А) расходится.
.
Следовательно, по необходимому условию
сходимости, ряд (А) расходится.![]()
Заметим, что в случае k=1 заключения о сходимости ряда сделать нельзя.
Например, ряд
![]() расходится,
расходится,![]() ,
,
а ряд
![]() сходится,
сходится,![]()
![]() .
.
Пример.
![]() .
.
Δ 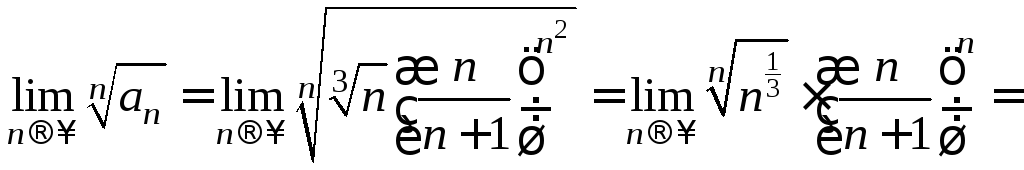
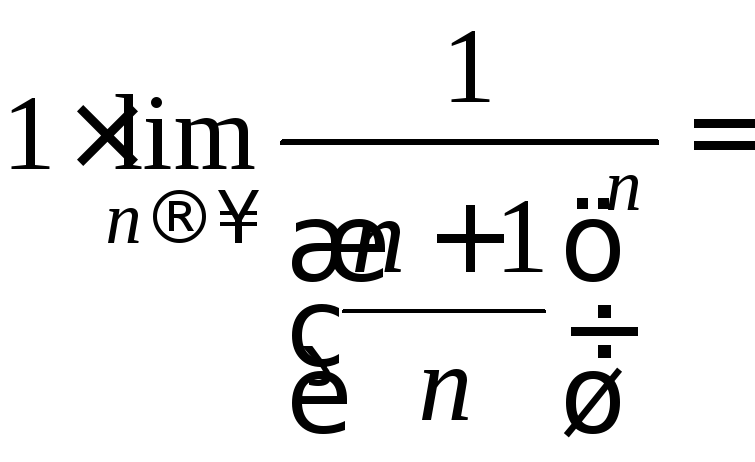
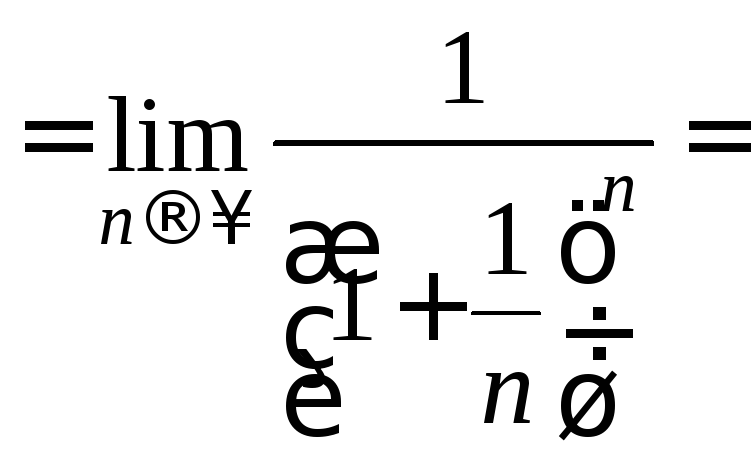
![]() .
.
Следовательно, ряд сходится. Δ
В случае, когда признак Даламбера дает ответ на вопрос о сходимости ряда, ответ может быть получен и с помощью признака Коши. Но признак Коши сильнее, чем признак Даламбера. В тех случаях, когда признак Даламбера не работает (d=1), ответ может получиться с помощью признака Коши.
Теорема 11
(интегральный
признак Маклорена-Коши). Пусть
![]() – положительный ряд. Если существует
невозрастающая непрерывная неотрицательная
функция
– положительный ряд. Если существует
невозрастающая непрерывная неотрицательная
функция![]() ,
заданная при
,
заданная при![]() ,
такая, что
,
такая, что![]() ,
то для сходимости ряда
,
то для сходимости ряда![]() необходимо и достаточно существование
несобственного интеграла
необходимо и достаточно существование
несобственного интеграла![]() .
.
Доказательство.
![]() Возьмем
Возьмем
![]() .
Рассмотрим
.
Рассмотрим![]() на
на![]() .
.
Так как
![]() не возрастает, то
не возрастает, то![]() выполнено
выполнено
![]() .
.
Проинтегрируем
это неравенство по отрезку
![]() :
:
![]() ,
,
или
![]() .
.
Так как по условию
![]() ,
то
,
то .
.
Просуммируем
последнее неравенство по
![]() :
:
![]()
Так как
![]() ,
,![]() ,
то получаем
,
то получаем
![]()
 . (13)
. (13)
Геометрическая
интерпретация неравенства (13): площадь
криволинейной трапеции, выражающаяся
определенным интегралом
![]() ,
ограничена по величине между площадями
вписанной и описанной ступенчатых
фигур.
,
ограничена по величине между площадями
вписанной и описанной ступенчатых
фигур.
Площадь вписанной
фигуры равна сумме площадей прямоугольников
шириной 1 и высотой
![]() .
То есть
.
То есть![]() .
Площадь описанной фигуры аналогично
.
Площадь описанной фигуры аналогично![]() .
Следовательно, получаем неравенство
(13).
.
Следовательно, получаем неравенство
(13).
1) Необходимость.
Пусть сходится
ряд
![]() .
Тогда по теореме 6
.
Тогда по теореме 6![]() ограничена, и из (13) следует, что
последовательность интегралов
ограничена, и из (13) следует, что
последовательность интегралов ограничена. Так как
ограничена. Так как![]() иn
возрастает, то эти интегралы образуют
возрастающую числовую последовательность.
Следовательно, существует предел этой
последовательности интегралов
иn
возрастает, то эти интегралы образуют
возрастающую числовую последовательность.
Следовательно, существует предел этой
последовательности интегралов
![]() .
То есть существует несобственный
интеграл
.
То есть существует несобственный
интеграл![]() .
.
2) Достаточность.
Пусть существует
несобственный интеграл
![]() .
Тогда последовательность интегралов
.
Тогда последовательность интегралов![]() возрастает (так как
возрастает (так как![]() )
и ограничена сверху, например, своим
пределом:
)
и ограничена сверху, например, своим
пределом:
 .
.
Из (13)
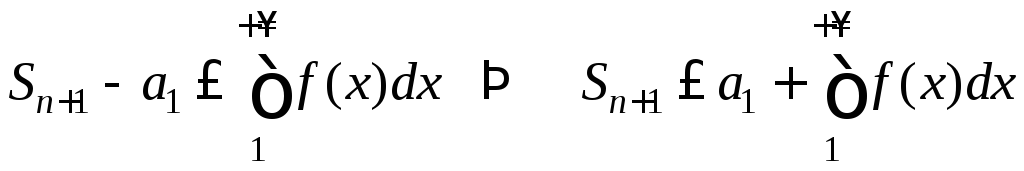 ,
,
то есть
последовательность
![]() ограничена сверху. По теореме 6 это
означает, что ряд
ограничена сверху. По теореме 6 это
означает, что ряд![]() сходится.
сходится.![]()
Замечание. Теорема
11 справедлива и для случая
![]() .
.
Пример. Исследовать
на сходимость гармонический ряд
![]() .
.
Δ Функция
![]() неотрицательна, непрерывна, не возрастает
на
неотрицательна, непрерывна, не возрастает
на![]() .
.
1) При 1 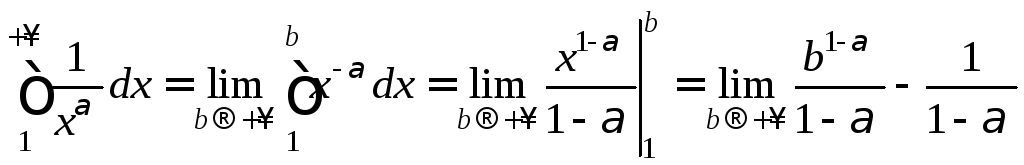 .
.
а) Если
![]() ,
то
,
то
![]() и
и![]() ,
то есть интеграл сходится. Значит,
гармонический ряд сходится.
,
то есть интеграл сходится. Значит,
гармонический ряд сходится.
б) Если
![]() ,
то
,
то
![]() ,
то есть интеграл расходится. Значит,
ряд
,
то есть интеграл расходится. Значит,
ряд![]() расходится.
расходится.
2) При
![]() ,
получаем основной гармонический ряд
,
получаем основной гармонический ряд
![]() .
.
![]() интеграл расходится,
интеграл расходится,
![]() ряд
расходится.
ряд
расходится.
Итак,
![]() сходится
при
сходится
при![]()
расходится при
![]() .
Δ
.
Δ
