Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Вятский государственный университет

Факультет автоматики и вычислительной техники

Кафедра электропривода и автоматизации промышленных установок

Автоматизация и оптимизация технологических процессов

Методические указания по выполнению контрольных заданий для студентов заочного отделения специальности 1804 «Электропривод и автоматизация промышленных установок»

Киров 2005

Печатается по решению редакционно-издательского совета

Вятского государственного университета

УДК 621.906

А88

Составители: доктор технических наук, профессор В.С. Хорошавин, преподаватель кафедры ЭПиАПУ Д.В. Пивоваров.

Редактор Е.Г. Козвонина

Подписано в печать Усл.печ.л. 1,6

Бумага офсетная Печать копир Aficio 1022

Заказ № 84 Тираж 25 Бесплатно

Текст напечатан с оригинал-макета, предоставленного составителем.

610000, г. Киров, ул. Московская, 36.

Оформление обложки, изготовление – ПРИП ВятГУ.

© Вятский государственный университет, 2005

1. Общие сведения

При выполнении первого контрольного задания студенты должны решить задачу с применением приближенных методов поиска экстремума функции многих переменных без ограничений или с ограничениями. Варианты заданий и требования к оформлению отчета изложены в методических указаниях «Автоматизация и оптимизация технологических процессов: программа, методические указания и контрольные задания для студентов з/о специальности 1804».

Задачи поиска экстремума функции относятся к задачам статической оптимизации режимов работы технологических процессов, в которых уравнения цели или критерия качества и уравнения ограничивающих связей, отражающих математическое описание объекта управления, являются алгебраическими.

Все задачи статической оптимизации технологических процессов делятся на 2 класса:

1. Задачи без ограничений, в которых требуется найти минимум (или максимум) функции многих переменных при отсутствии ограничений на переменные:

, ,

где – открытое множество;

2. Задачи с ограничениями, в которых отыскивается экстремум функции 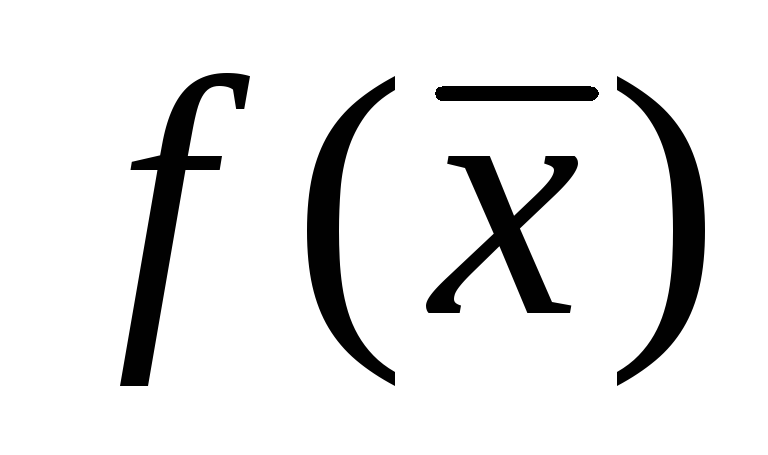при ограничениях.

Вторая задача весьма общая, поэтому она конкретизируется следующим образом:

• если функци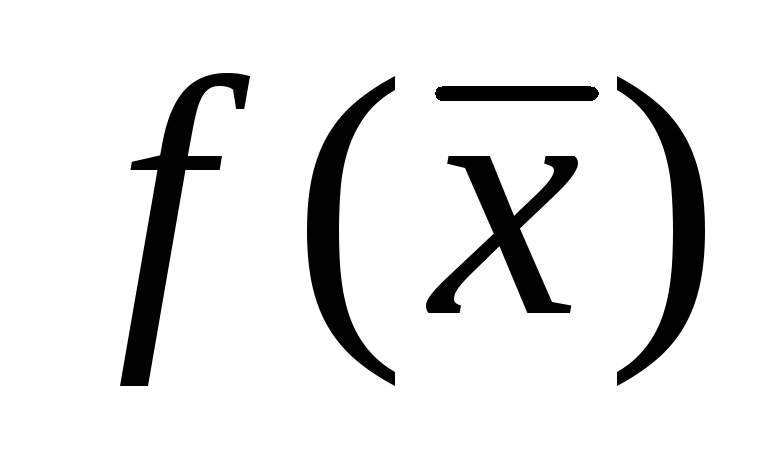и и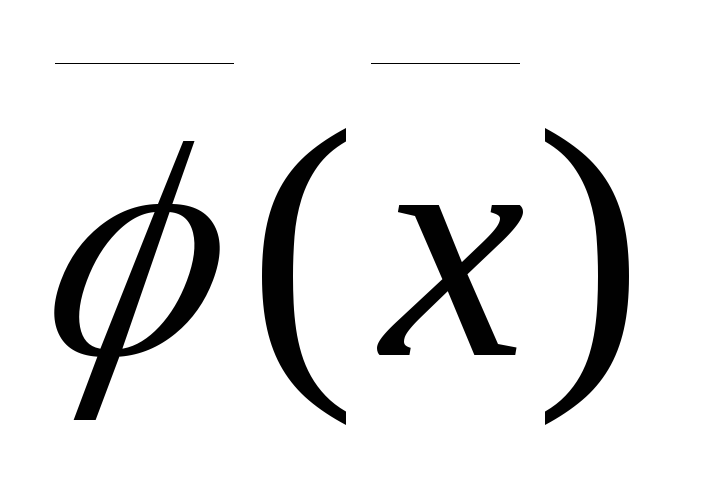линейны по переменным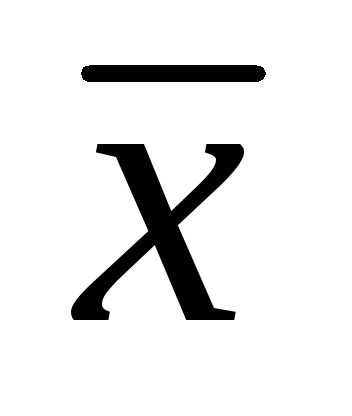, то имеем задачу линейного программирования;

• если ограничения заданы в форме равенств 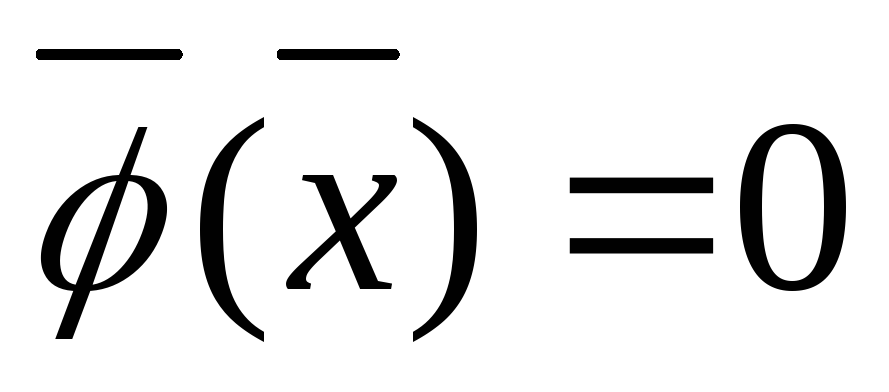, то такая задача называется классической задачей Лагранжа на условный экстремум;

• если ограничения заданы в форме неравенств или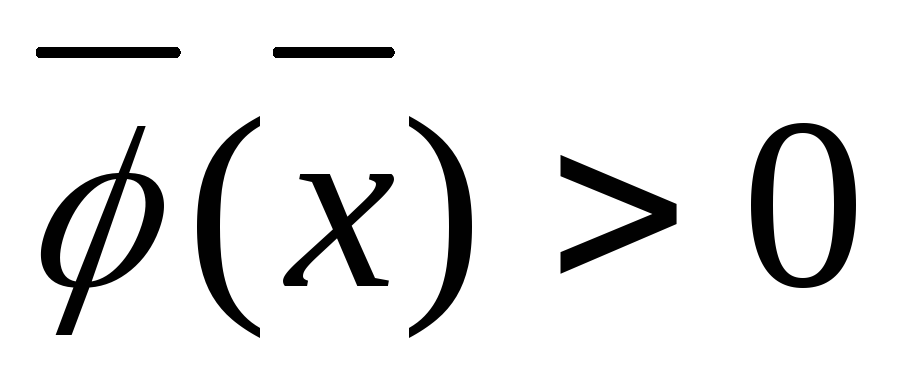, то такая задача называется неклассической задачей Лагранжа на условный экстремум.

• неклассическая задача в свою очередь подразделяется на задачи квадратичного, выпуклого и нелинейного программирования в зависимости от вида функции и ограничений.

Все поставленные задачи объединяются общим термином – задачи математического программирования.

2. Предварительный анализ функций для применения численных методов

Прежде чем приступать к численному поиску экстремума функции, необходимо провести качественное исследование функции, т.к. без предварительного анализа свойств функции численные методы поиска экстремума могут не дать желаемых результатов.

2.1. В инженерной практике уравнение цели, а также реальные снятые или полученные аналитически характеристики объекта управления, как правило, аппроксимируются уравнениями не выше второго порядка.

Квадратичные функции представляются в виде уравнения поверхности второго порядка, которые в матричном виде записываются так:

, (1)

Частным случаем квадратичной функции является квадратичная форма:

Матрица в выражении (1) представляет собой матрицу Гессе – аналог второй производной для функций многих переменных (см. ниже).

Например, функция при записи по форме (1) примет следующие значения параметров:, С=(1,1),,.

2.2. Необходимым условием существования экстремума функции многих переменных в точке х^*является равенство в ней нулю частных производных первого порядка, т.е. в точке х^*справедлива система уравнений (2). Решение этой системы уравнений зависит от вида функции.

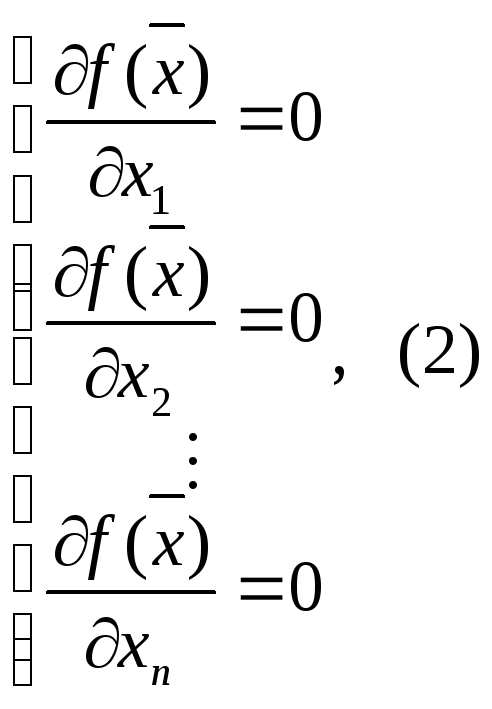
Для квадратичных функций экстремальные точки определяются из решения системы линейных уравнений вида:

.

Решение системы линейных уравнений не вызывает проблем при хорошо обусловленной матрице Н, когда ее определитель не мал и не велик, как и ее элементы. Но хорошо обусловленные матрицы получаются не всегда при реальных аппроксимациях. Кроме того, операция обращения матрицы довольно громоздкая. Поэтому для поиска экстремума ФМП широкое распространение получили приближенные (численные) методы поиска экстремума. Вторая причина – возможность использования численных методов в автоматических устройствах.

2.3. Численные методы нахождения экстремума функции многих переменных удобнее иллюстрировать на плоскости, чем в пространстве. С этой целью вводится понятие линий уровня.

Л

Рис. 1

инии уровня функцииполучаются из уравнения. Геометрически дляэто означает, что поверхность рассекается плоскостями, параллельными плоскости (х₁, х₂). В этих плоскостях образуются линии, которые проеци­руются на плоскость (х₁, х₂). Проекции этих линий называются линиями уровня.

Описанное иллюстрируется рисунком 1.

2

Рис. 2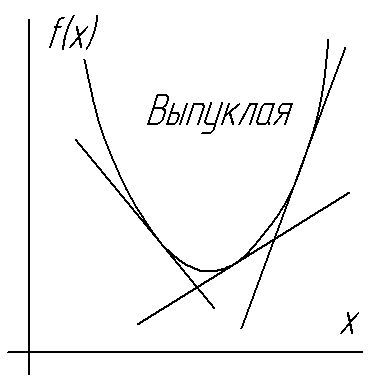

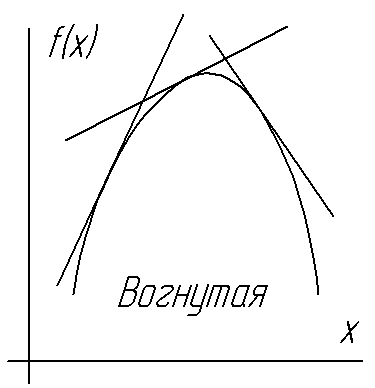
.4. Определение единствен­ности экстремума и его характера, т.е. минимум или максимум. Установление указанных свойств выполняется на основе понятий о выпуклости и вогнутости функций. Свойством выпуклых и вогнутых функций является то, что на открытом интервале они имеют единственный экстремум.

Примеры выпуклых и вогнутых функций показаны на рис. 2.

Вопрос определения характера экстремума – минимум или максимум – как известно можно определить по знаку второй производной, если в точке экстремума вторая производная положительная, то это минимум, иначе – максимум. Аналогичным образом решается вопрос о минимуме/максимуме для функции многих переменных. Аналогом второй производной является матрица Гессе, образованная как вторая производная функции по переменнымв предполагаемой точке экстремума:

Данная матрица получила название матрицы Гессе, которая является аналогом второй производной для функций одной переменной. Поэтому по знаку матрицы Гессе можно судить о минимуме или максимуме функции, что значительно проще, чем определять это из определения выпуклости или вогнутости функции.

Если матрица Гессе положительно определена для любых , то– строго выпуклая и имеет единственный минимум, если же матрица Гессе отрицательно определена для любых, тоявляется строго вогнутой и имеет единственный максимум.

Положительную или отрицательную определенность гессиана можно установить двумя способами.

Первый способиспользует критерий Сильвестра, который исследует знаки всех главных миноров Н. Если все главные миноры Н положительны, то матрица Н положительно определена и имеет место выпуклая функция с единственным минимумом. Если же главные миноры отрицательны, то Н отрицательно определена и имеем вогнутую функцию с единственным максимумом.

Второй способустанавливает выпуклость или вогнутость функции на базе собственных чисел матрицы Н. Если все собственные числа больше 0, то функция выпуклая, если меньше нуля, то вогнутая.