- •Физический практикум по оптике
- •«Волновая и квантовая оптика»
- •Введение
- •Изучение законов теплового излучения
- •Контрольные вопросы
- •Дифракционная решетка
- •Контрольные вопросы
- •Интерферометрический метод измерения малых деформаций и показателя преломления
- •15.Рассчитайте модуль Юнга для каждой нагрузки по формуле
- •16.Окончательный результат для е запишите в виде , где– абсолютная погрешность; – среднее арифметическое значение модуля Юнга.
- •Контрольные вопросы
- •Интерференция в тонких пленках
- •Контрольные вопросы
- •Лабораторная работа № 60 изучение основных законов фотоэффекта
- •1. Фотоэффект наблюдается под действием ультрафиолетового излучения.
- •2. Сила тока возрастает с увеличением освещенности пластины.
- •3. Испускаемые пластиной под действием света частицы имеют отрицательный заряд.
- •4. Эффективность фотоэффекта зависит от химической природы и состояния поверхности металлической пластины.
- •Контрольные вопросы
- •Лабораторная работа № 61 изучение явления естественного вращения плоскости полярицазии света
- •Контрольные вопросы
- •Лабораторная работа № 65 поляризация света
- •Контрольные вопросы
- •Содержание
- •Физический практикум по оптике
- •«Волновая и квантовая оптика»
- •Компьютерная верстка о.Л.Никонович
Контрольные вопросы
Какое излучение называется тепловым?
Дайте определения величин, характеризующих тепловое излучение.
Дайте определение абсолютно черного и серого тела.
Запишите законы Кирхгофа, Стефана – Больцмана, Вина и объясните физический смысл входящих в них величин
В чем заключается метод оптической пирометрии и для чего он применяется?
Перечислите виды температур, получаемых методами оптической пирометрии, и дайте им определение.
Лабораторная работа № 55
Дифракционная решетка
Цель работы: наблюдение дифракции света, определение длины световой волны с помощью дифракционной решетки.
Приборы и принадлежности:
осветительное устройство
дифракционная решетка с d =1/600 мм или d =1/100 мм
оптическая скамья
2 держателя
линейка
Теоретическое введение
Дифракцией называется любое отклонение распространения света от прямолинейного, не связанное с отражением и преломлением. Качественный метод расчета дифракционной картины предложил Френель. Основной идеей метода является принцип Гюйгенса - Френеля:
Каждая точка, до которой доходит волна, служит источником когерентных вторичных волн, а дальнейшее распространение волны определяется интерференцией вторичных волн.
Геометрическое место точек, для которых колебания имеют одинаковые фазы, называют волновой поверхностью. Волновой фронт также является волновой поверхностью.
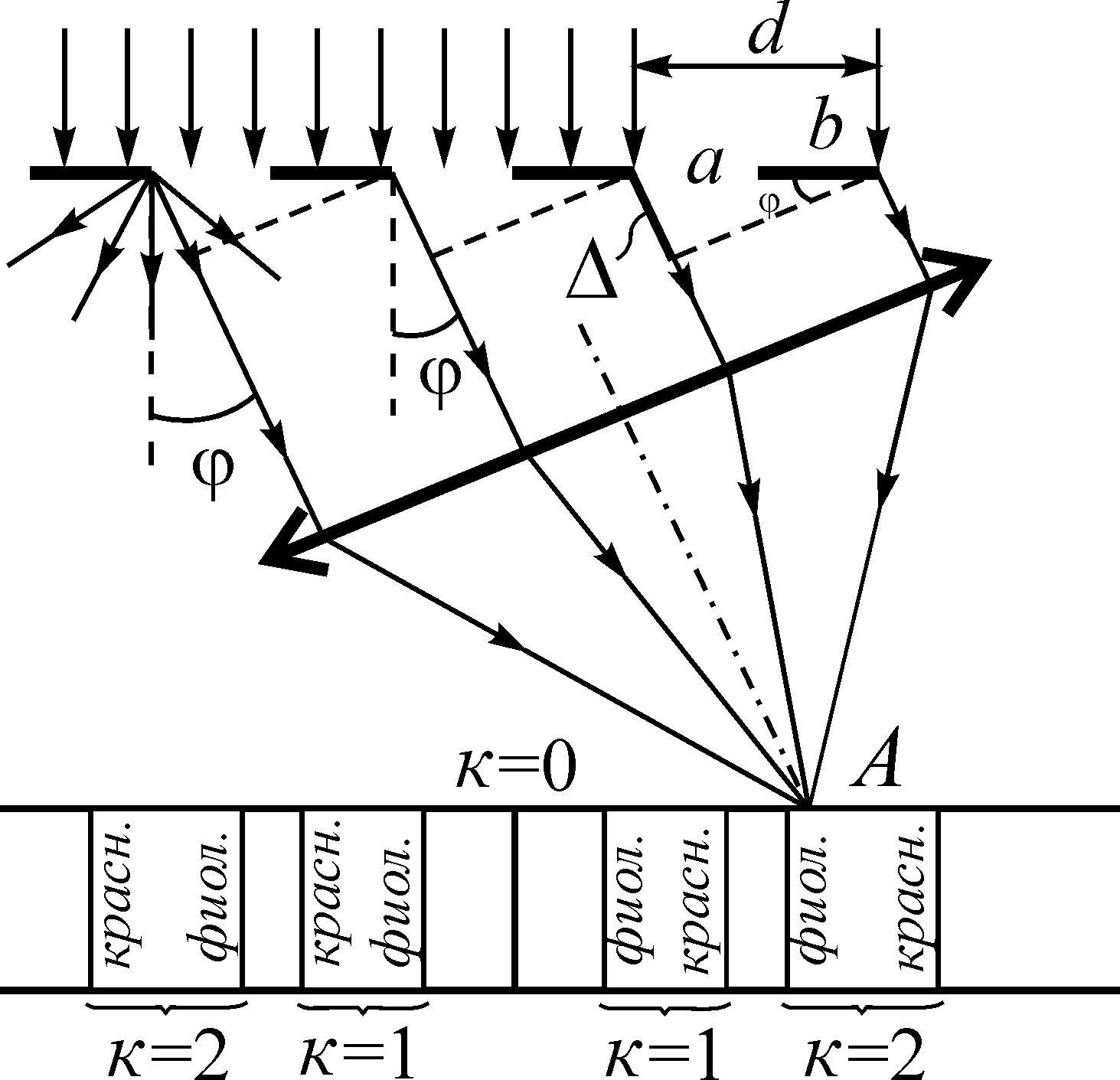
Дифракционная решетка представляет собой совокупность большого числа параллельных щелей или зеркал одинаковой ширины и отстоящих друг от друга на одинаковом расстоянии. Периодом решетки (d) называется расстояние между серединами соседних щелей, или что то же самое сумма ширины щели (а) и непрозрачного промежутка (b)между ними (d = a + b).
Рассмотрим принцип действия дифракционной решетки. Пусть на решетку нормально к её поверхности падает параллельный пучок лучей белого света (рис. 1). На щелях решетки, ширина которых соизмерима с длиной волны света, происходит дифракция.
|
|
|
Рис. 1. Ход лучей в дифракционной решетке |
![]() ,
(1)
,
(1)
где φ – угол отклонения луча решеткой.
Следовательно, условие возникновения главных интерференционных максимумов решетки или уравнение дифракционной решетки
![]() ,
(2)
,
(2)
где λ – длина световой волны.
В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, κ = 0), справа и слева от которого располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков (рис. 1). Интенсивность максимумов уменьшается с ростом их порядка, т.е. с увеличением угла дифракции.
Уравнение (1) позволяет рассчитать длину волны падающего света, если измерен угол дифракции φ, для данной спектральной линии, известны период дифракционной решетки d и порядок спектра k.
Зная период решетки, можно рассчитать число штрихов n, нанесенных на 1 мм ширины решетки:
![]() .(3)
.(3)
Одной
из основных характеристик дифракционной
решетки является её угловая дисперсия.
Угловая дисперсиярешетки определяет
угловое расстояниеdφ
между направлениями для двух
спектральных линий, отличающихся по
длине волны на 1 нм (![]() = 1 нм),
и характеризует степень растянутости
спектра вблизи данной длины волны:
= 1 нм),
и характеризует степень растянутости
спектра вблизи данной длины волны:
![]() .
(4)
.
(4)
Формула для расчета
угловой дисперсии решетки может быть
получена при дифференцировании уравнения
(2)
![]() .
Тогда
.
Тогда
![]() .
(5)
.
(5)
Из формулы (5) следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра.
Для решеток с
разными периодами ширина спектра больше
у решетки, характеризующейся меньшим
периодом. Обычно в пределах одного
порядка
![]() меняется незначительно (особенно для
решеток с небольшим числом штрихов на
миллиметр), поэтому дисперсия в пределах
одного порядка почти не меняется. Спектр,
полученный при постоянной дисперсии,
растянут равномерно во всей области
длин волн, что выгодно отличает спектр
решетки от спектра, даваемого призмой.
меняется незначительно (особенно для
решеток с небольшим числом штрихов на
миллиметр), поэтому дисперсия в пределах
одного порядка почти не меняется. Спектр,
полученный при постоянной дисперсии,
растянут равномерно во всей области
длин волн, что выгодно отличает спектр
решетки от спектра, даваемого призмой.
Угловая дисперсия
связана с линейной дисперсией
![]() .
Линейную
дисперсию можно также вычислить по
формуле
.
Линейную
дисперсию можно также вычислить по
формуле
![]() ,
(6) где
,
(6) где
![]() – линейное расстояние на экране или
фотопластинке между спектральными
линиями,f
– фокусное расстояние линзы.
– линейное расстояние на экране или
фотопластинке между спектральными
линиями,f
– фокусное расстояние линзы.
Дифракционная решетка также характеризуется разрешающей способностью. Эта величина, характеризующая способность дифракционной решетки давать раздельное изображение двух близких спектральных линий
R
=
![]() ,
(7)
,
(7)
где – средняя длина волны разрешаемых спектральных линий;– разность длин волн двух соседних спектральных линий.
Зависимость разрешающей способности от числа щелей дифракционной решетки N определяется формулой
R
=![]() =
kN,
(8)
=
kN,
(8)
где k – порядок спектра.
Из уравнения для дифракционной решетки (1) можно сделать следующие выводы:
Дифракционная решетка будет давать заметную дифракцию (значительные углы дифракции) только в том случае, когда период решетки соизмерим с длиной световой волны, то есть d 10 –4 см. Решетки с периодом меньше длины волны не дают дифракционных максимумов.
Положение главных максимумов дифракционной картины зависит от длины волны. Спектральные составляющие излучения немонохроматического пучка отклоняются решеткой на разные углы (дифракционный спектр). Это позволяет использовать дифракционную решетку в качестве спектрального прибора.
Максимальный порядок спектра, при нормальном падении света на дифракционную решетку, определяется соотношением:
kmax d .
Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем и частотой штрихов, что позволяет перекрыть область спектра от ультрафиолетовой его части ( 100 нм) до инфракрасной ( 1 мкм). Широко используются в спектральных приборах гравированные решетки (реплики), которые представляют собой отпечатки решеток на специальных пластмассах с последующим нанесением металлического отражательного слоя.
Описание установки
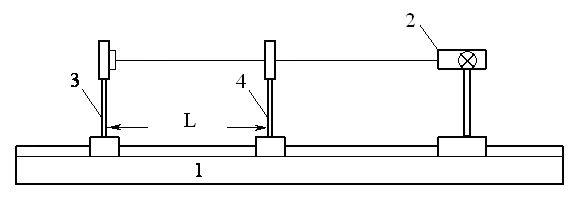
Схема установки изображена на рис. 2.
|
|
|
Рис. 2. |
На оптической скамье 1 располагаются: источник световых волн (лампа) 2; перемещаемый вдоль скамьи держатель 3, на котором закрепляется дифракционная решетка; держатель 4, на котором закрепляется миллиметровая линейка и экран с узкой вертикальной щелью посередине. Расстояние между щелью и дифракционной решеткой изменяют, перемещая держатель 3.
В эксперименте в качестве источника света используется люминесцентная лампа. Свет от лампы проходит через щель в экране и попадает на дифракционную решетку. Дифракционную картину наблюдают без вспомогательных линз, приблизив глаз к дифракционной решетке. Фокусировка света происходит непосредственно на сетчатке глаза. Дифракционную картину (совокупность спектральных линий) наблюдаем на фоне экрана с линейкой. Совокупность спектральных линий представляет собой дифракционный спектр.
Длину световой волны определяем из формулы (2).
![]() ,
(9)
,
(9)
где φ – угол дифракции, d – период дифракционной решетки, λ – длина волны, соответствующая наблюдаемой линии.
Из рисунка 3 видно,
что
![]() ,
следовательно,
,
следовательно,![]()
|
|
|
Рис. 3. Схема для наблюдения дифракционной картины |
Подставив в формулу (9) выражение для φ получим:
![]() (10)
(10)
Порядок выполнения работы
Установить лампу на оптическую скамью (рис.2).
Установить на оптической скамье держатели 3 и 4 (рис.2)
Поместить в держатель 3 рамку с дифракционной решеткой (d = 1/600 мм или d = 1/100 мм).
Перемещая держатель 3 по оптической скамье установить так, чтобы при рассмотрении щели через дифракционную решетку на экране были видны линии спектра.
Вращая ручку регулировки ширины щели на держателе 4 добиться чёткого изображения спектральных линий.
Выбрать одну из наиболее ярких линий в спектрах первого, второго и т.д. порядков.
Измерить расстояние, а от центра щели до выбранной линии по линейке на экране в правом и левом спектре. Для увеличения точности измерения следует располагать экран со щелью на таком расстоянии, чтобы спектральная линия совпадала с одним из штрихов линейки, закрепленной на экране. Данные записать в таблицу 1.
Измерить расстояние L между решеткой и линейкой на экране со щелью, полученное значение записать в таблицу 1.
Изменяя расстояние между экраном со щелью и решеткой, повторить п. 7-8 еще 4 раза.
Выбрать еще одну или две ярких линии и повторить пп. 7-9.
Для каждого измерения по формуле (13) вычислить длину волны λ и занести в таблицу 1.
Таблица 1
|
Цвет линии |
Порядок спектра |
Номер измерения |
апр, мм |
алев, мм |
|
L, мм |
λ, мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
Рассчитать угловую дисперсию дифракционной решётки по формуле
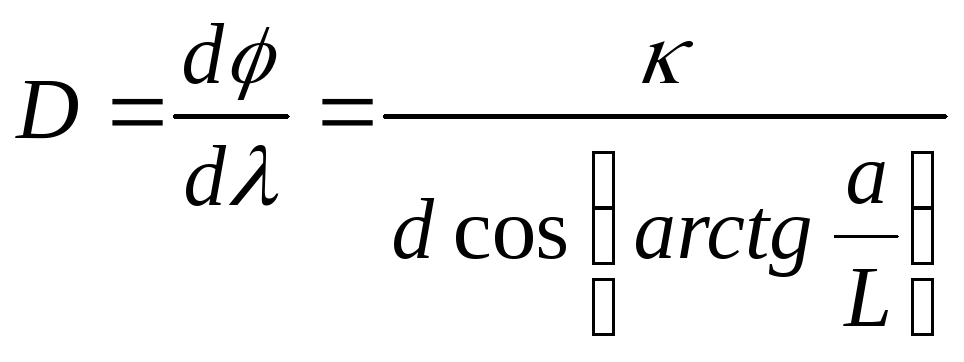 .
.Рассчитать абсолютную и относительную погрешности длины волны, как для прямых измерений.
Полученные значения длин волн сравнить с табличными и сделать выводы.