Алгоритм приведения к СДНФ

•Рассматриваем только те строки таблицы истинности данной функции, в которых функция принимает значение 1.

•Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем аргумент, принимающий значение 0, входит в нее с отрицанием; значение 1 – без отрицания.

•Наконец, образуем дизъюнкцию всех полученных конъюнкций.

Конъюнктивно-нормальная форма

КНФ — является логическим произведением элементарных дизъюнкций.

Совершенная КНФ – логическое произведение элементарных дизъюнкций, в каждой из которых присутствуют все переменные данной функции.

Алгоритм приведения к СКНФ

•Составляем таблицу истинности данной функции.

•Рассматриваем только те строки таблицы, в которых функция принимает значение 0.

•Каждой такой строке соответствует дизъюнкция всех аргументов (без повторений). Причем аргумент, принимающий значение 0, входит в нее без отрицания; значение 1 – с отрицанием.

•Наконец, образуем конъюнкцию всех полученных дизъюнкций.

Любая булева функция, не являющаяся тождественным нулём или единицей, имеет только одну СДНФ с точностью до расположения переменных.

	х1 х2 х3			F
	0	0	0	0
Задача. Пусть при n= 3	0	0	1	0
булева функция задана таблицей	0	1	0	1
истинности. Составить СДНФ	0	1	1	1
и СКНФ для данной функции.	1	0	0	0
	1	0	1	0
	1	1	0	1
	1	1	1	0

СДНФ: по	строкам,
в которых	булева функция

принимает значение 1, составляем элементарные конъюнкции, которые затем соединяем дизъюнкциями. В конъюнкцию входит сама переменная, если её значение в данной строке равно 1, и отрицание этой

переменной, если её значение равно 0.

х1	х2	х3	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

F (x1 , x2 , x3 ) x1 x2 x3 x1 x2 x3 x1 x2 x3

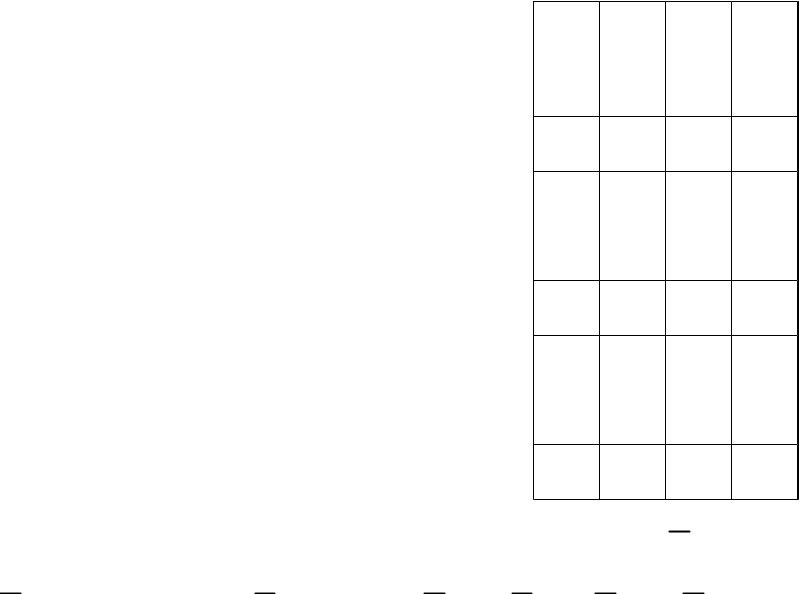
СКНФ: по	строкам,
в которых	булева функция

принимает значение 0, составляем элементарные дизъюнкции, которые затем соединяем

конъюнкциями. В дизъюнкцию входит сама переменная, если её значение в данной строке равно 0, и отрицание этой

переменной, если её значение равно 1.

х1	х2	х3	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

F (x1 , x2 , x3 ) x1 x2 x3 x1 x2 x3

x1 x2 x3 x1 x2 x3 x1 x 2 x3

Существование СДНФ позволяет провести процедуру, называемую разложением булевой

функции по переменной xk . Разложение позволяет представить произвольную функцию

f (x1 ,..., xn ) в виде

f (x1,..., xn ) xk p(x1,..., xk 1, xk 1,..., xn ) xk q(x1,..., xk 1, xk 1,..., xn )

p и q – функции, не зависящие от xk .

Пример. F(x1 , x2 , x3 ) x1 x2 x1 x2 x3

Функция разложена по переменной x1 .

q(x2 ) x2

p(x2 , x3 ) x2

x

3

Задача. По заданной таблице истинности найти логическую функцию.

	Решение. Составим СДНФ:																																							х1		х2	х3	F
F(x1, x2 , x3 )								1		2				3						1			2 x3						1x2				3 x1				2 x3.
							x		x			x						x				x						x			x				x					0	0 0 1
Минимизируем полученную																																								0		0	1	1
функцию, предварительно
																																								0		1	0	1
разложив её по переменной x3																																					:
																																								0		1	1	0
x3		1		2 x1		2							3				1				2					1x2						2 x3				1			3.
	x		x		x						x					x			x					x						x				x				x		1	0 0 0
Здесь был применён закон																																								1		0	1	1
алгебры логики – закон
																																								1		1	0	0
склеивания:																											a .
															ab ab																									1		1	1	0

Теорема.

Всякая истинностная функция, не равная тождественно Л, может быть представлена в СДНФ.

Всякая истинностная функция, не равная тождественно И, может быть представлена в СКНФ

СДНФ или СКНФ ?

Если условиться из двух форм, СДНФ и СКНФ, отдавать предпочтение той, которая содержит меньше букв, то

•СДНФ предпочтительней, если в столбце значений функции таблицы истинности меньше единиц;

•СКНФ – если в этом столбце меньше нулей.

Полные системы истинностных функций

Система истинностных функций называется полной, если с помощью функций этой системы можно выразить любую истинностную функцию.

Система { , . } — полная (так как СДНФ, СКНФ содержат только функции этой системы)