Обозначим

 

  а  ,      (II.24)

 

тогда:

 

,  m =1, 2, 3, ....      (II.25)

 

Поскольку функции  {Ф_n}  известны, то известными можно считать и величины  , и поэтому систему уравнений  (II.25)  можно использовать для нахождения коэффициентов  {c_n}  и тем самым - функции  .  

 

В развернутом виде систему уравнений  (II.25)  можно записать как

 

      (II.26)

 

Из линейной алгебры известно, что эта система уравнений имеет нетривиальные решения только тогда, когда детерминант

 

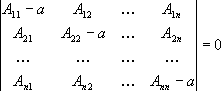      (II.27)

 

Раскрывая этот детерминант и решая его относительно параметра a,  подставляя затем результат в  (II.26), мы можем определить все коэффициенты разложения {c_m} и тем самым - неизвестную функцию  .

 

На этом мы можем считать законченным знакомство с основными, чисто математическими особенностями аппарата квантовой механики и вернутся к способам рассмотрения реальных физических ситуаций. Выше говорилось, что состояние микрообъекта можно описать путем задания волновой функции, а далее мы довольно много говорили об основах операторного исчисления. Естественно, нас интересует, естественно, не операторы как абстрактные математические объекты, а реальные физические величины, которые можно измерить в ходе эксперимента. Поэтому давайте вспомним

 Постулат №3.

 Всякой физической величине L в квантовой механике сопоставлен линейный самосопряженный оператор. Единственно возможными величинами, которые может иметь эта физическая величина, являются собственные значения l операторного уравнения LY=lY

 

Необходимо отметить, что между операторами, как правило, сохраняются те же соотношения, которые имеют место между физическими величинами и в классической механике.

 

Для некоторых простейших и важнейших физических величин операторы можно выписать без всякого труда:

 

координата                     x ® x=x
время                             t ® t=t
составляющая импульса   px ® px=ihd/dx	(II.28)
кинетическая энергия  T=p^2/2m ® h^2/2m(d^2/dx^2+d^2/dy^2+d^2/dz^2)

 

Окончательную же связь между физическими величинами и соответствующими операторами можно установить на основе

 Постулат №4.

 Возможная волновая функция состояния системы Y получается при решении или нестационарного дифференциального уравнения ih·dY/dt=HY, или стационарного, независящего от времени операторного уравнения HY=EY, где H - оператор Гамильтона, E - энергия системы, а уравнение называется уравнением Шредингера.

                                                                                       (II.29)

 

Постулат №5.

 

Если произвести многократные измерения какой-либо динамической переменной l системы, находящейся в состоянии Y, то на основании результатов этих измерений можно определить ее среднюю величину. Эта средняя величина вычисляется по формуле:

l=òY^*LYdq/òY^*Ydq

                                                                                        (II.30)

 

Эти два положения можно скомбинировать, предположив, что

 

                 (II.31),

где  c_n  - некоторые коэффициенты, и тогда среднее значение величины  L  будет равно:

 

                                  (II.32)

 

другими словами, величина  есть вероятность того, что в момент измерения наблюдаемой величины  L  будет получено значение , соответствующее волновой функции  уравнения на собственные значения (II.29).

 

Необходимо сформулировать и еще одно важнейшее свойство:

 

Необходимым и достаточным условием того, что две измеряемые физические величины L и M могут одновременно принимать в результате измерения точные значения l_i  и  m_i является коммутативность соответствующих операторов L и M

 

Это положение устанавливает связь математического аппарата квантовой механики с одним из основополагающих ее принципов - принципом неопределенности Гейзенберга и имеет очень большое значение при проведении каких-либо расчетов, поскольку из него следует, что коммутирующие операторы имеют общую систему собственных функций, что безусловно упрощает процедуры получения волновых функций сложных операторов.

 

Выше мы приводили операторы, соответствовавшие основным физическим величинам. Однако известно, что часто микрообъекты дополнительно характеризуются величинами, не имеющими аналогов в классической механике. Примером такой величины может быть спин, который не зависит ни от координат, ни от импульсов. Спину соответствует оператор спина  S  и операторы проекций на оси координат, для которых справедливы коммутационные соотношения:

 

s_xs_y-s_ys_x=ihs_z

s_ys_z-s_zs_y=ihs_x                                         (II.33)

s_zs_x-s_xs_z=ihs_y

 

Позднее мы будем рассматривать операторы спина более подробно.