Fizika_Ekzamen_vip

38)Адиабатический процесс. Показатель адиабаты.

Адиабатный процесс - процесс сжатия или расширения газа, происходящий без теплообмена с окружающей средой.

Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:

A

(1).

С другой стороны, из уравнения Клапейрона-Менделеева следует:

A	(2).
Разделим уравнение (2) на уравнение (1):
A	, гдеA	.
Проинтегрируем полученное уравнение:
A	.
Таким образом, при адиабатном процессе

A — уравнение Пуассона.

С учетом уравнения Клапейрона-Менделеева уравнение Пуассона может быть представлено в виде:

A

или A

.

A

График адиабатного процесса — более крутая кривая, чем гипербола при изотермическом

процессе. Это следует из выражения производной A		, полученной из уравнения
Пуассона.
Работа газа при адиабатном процессе равна убыли внутренней энергии:
A	.

где γ — показатель адиабаты (коэффициент Пуассона).(из 36 билета)

39)Тепловые машины. КПД тепловой машины. Цикл Карно.

Тепловая машина

Тепловой машиной называется устройство, которое преобразует теплоту в работу или обратно и действует строго периодически, т. е. после завершения цикла возвращается в исходное состояние.

КПД тепловой машины

КПД тепловой машины называется отношение работы, произведенной этой машиной за один цикл, к теплоте, поглощенной в ходе рассматриваемого цикла.

Цикл Карно́— идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.

Кпд Карно равен -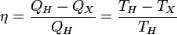

Пусть тепловая машина состоит из нагревателя с температурой , холодильника с температурой и рабочего тела.

Цикл Карно состоит из четырёх стадий:

1)Изотермическое расширение (на рисунке — процесс 1→2). В начале процесса рабочее тело имеет температуру Тн, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Qн. При этом объём рабочего тела увеличивается.

2)Адиабатическое расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3)Изотермическое сжатие (на рисунке — процесс 3→4). Рабочее тело, имеющее к тому времени температуру Tх, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Qх.

4)Адиабатическое сжатие (на рисунке — процесс 4→1). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

40)Барометрическая формула. Распределение Больцмана.

При изменении положения относительно оси Z в атмосфере меняется величина давления. Возьмем мысленное увеличение по оси Z, тогда давление уменьшится и:

−dp = ρgdh	PV = m RT
		M
	m	= mRT
	ρ	MP
dp = − MPg dh	ρ = mPM = PM
		mRT RT
RT
dp = − Mg dh
P	RT

Интегрируем(Температура не меняется)

ln p = − Mgh + ln C RT

Проецируем

p = C exp(− Mgh)

RT

При h = 0 →C = p0

p = p0 exp(− Mgh)

RT

Это и есть барометрическая формула.

Распределение Больцмана.

Распределение Больцмана получается из барометрическй формулы путем преобразований.

p = p0 exp(− Mgh)

RT

Т.к. AM = m , где m - масса молекулы, k - постоянная Больцмана и Ap = nkT ,Ap0 = n0 kT , то

R k

получим:

n = n0 exp(− mgh) kT

Здесь n - концентрация молекул на высоте h, An0 - концентрация молекул на высоте Ah0 =0.

εn = mgh

n = n0 exp(− εn ) kT

где A — потенциальная энергия молекулы. В однородном поле силы тяжести A

.

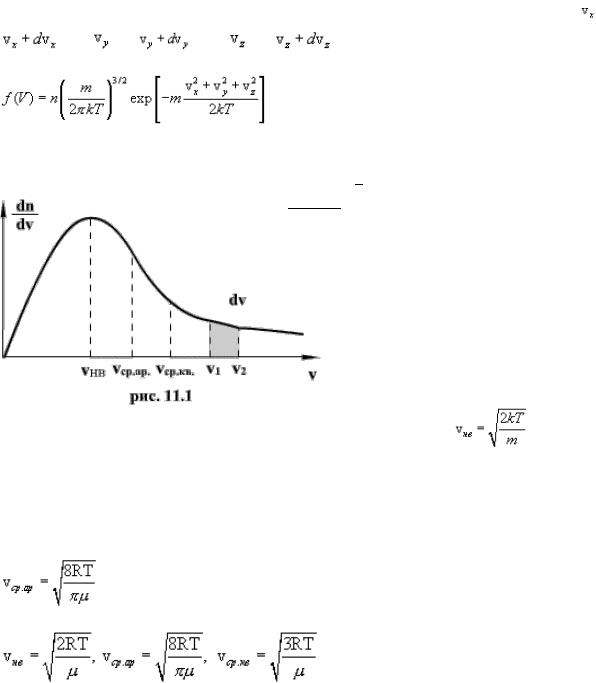
41)Распределение Максвелла молекул по скоростям.

Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2 . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число

молекул в единице объема; компоненты скоростей которых лежат в интервале от A до

A	, от A до A	и от A до A	, определяются функцией распределения
Максвелла

A

где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, что число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет

	вид	3		mv2
		m 2	−		2	dv
				2 kT
	dn = 4πn		e		v
		2πkT

Распределение Максвелла достигает максимума при скорости A , т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.

Кривая распределения Максвелла позволит найти среднюю арифметическую скорость

A . Таким образом,

A

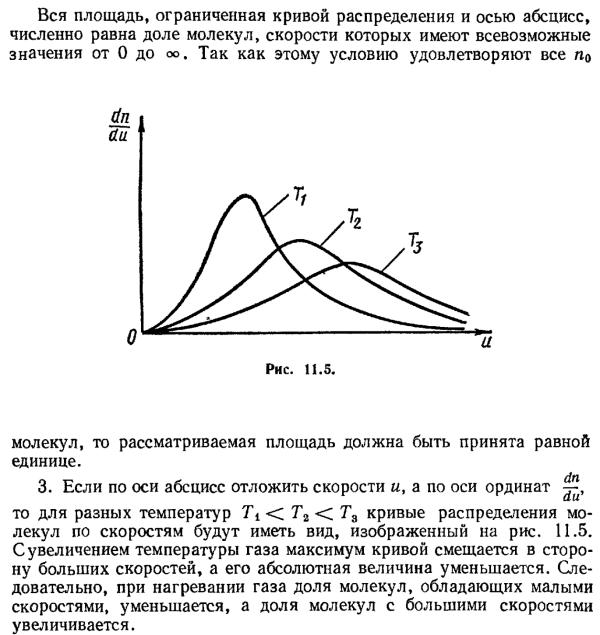
С повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.

A

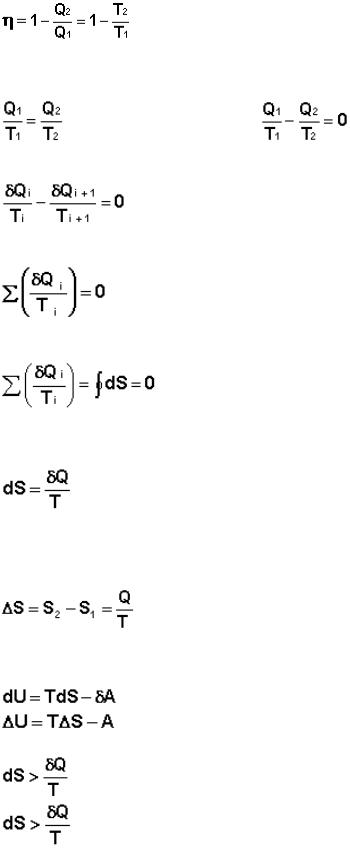
42)Энтропия и её свойства. Изопроцессы и цикл Карно в переменных T и S.

Мерой связанной энергии является новая термодинамическая функция состояния, называемая энтропией.

Введем определение энтропии, основываясь на цикле Карно. Преобразуем выражение (I.41) к следующему виду:

A

(I.45)

Отсюда получаем, что для обратимого цикла Карно отношение количества теплоты к температуре, при которой теплота передана системе (т.н. приведенная теплота) есть величина постоянная:

A (I.46) A (I.47)

Это верно для любого обратимого циклического процесса, т.к. его можно представить в виде суммы элементарных циклов Карно, для каждого из которых

A

(I.48)

Т.о., алгебраическая сумма приведённых теплот для произвольного обратимого цикла равна нулю:

A

(I.49)

Выражение (I.49) для любого цикла может быть заменено интегралом по замкнутому контуру:

A

(I.50)

Если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение есть полный дифференциал некоторой функции состояния; эта функция состояния есть

энтропия S:

A

(I.51)

Выражение (I.51) является определением новой функции состояния – энтропии и математической записью второго начала термодинамики для обратимых процессов. Если система обратимо переходит из состояния 1 в состояние 2, изменение энтропии будет равно:

A	(I.52)
Подставляя (I.51, I.52) в выражения для первого начала термодинамики (I.1, I.2) получим
совместное аналитическое выражение двух начал термодинамики для обратимых
процессов:
A	(I.53)
A	(I.54)
Для необратимых процессов можно записать неравенства:
A	(I.55)

A

(I.56)

A

(I.57)

Т.о., как следует из (I.57), работа обратимого процесса всегда больше, чем того же процесса, проводимого необратимо. Если рассматривать изолированную систему (δQ = 0), то легко показать, что для обратимого процесса dS = 0, а для самопроизвольного необратимого процесса dS > 0.

Свойства энтропии:

В изолированных системах самопроизвольно могут протекать только процессы, сопровождающиеся увеличением энтропии.

Энтропия изолированной системы не может самопроизвольно убывать.

Энтропия изолированной системы, находящейся в равновестном состоянии, максимальна. Оба этих вывода также являются формулировками второго начала термодинамики.

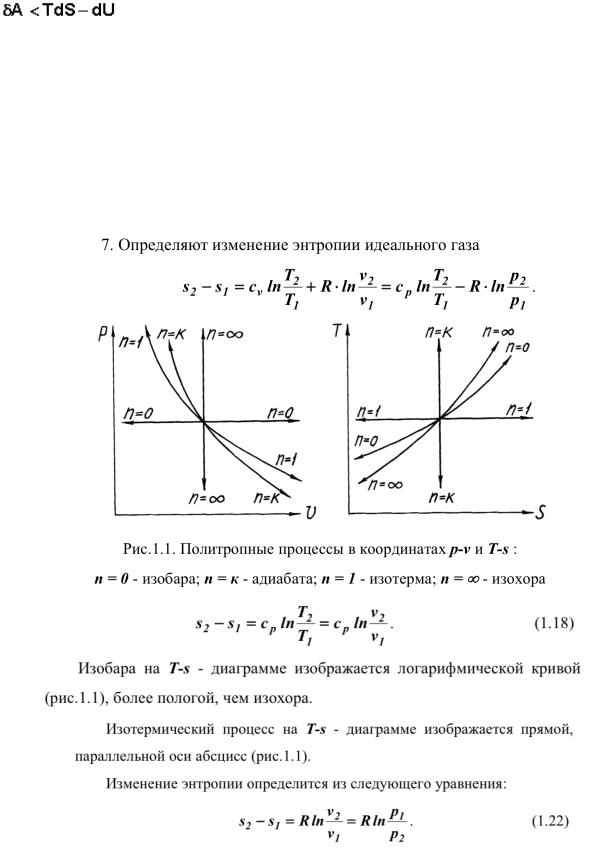
Энтропия в изопроцессах.