
- •1. Неопределенный интеглал и его свойства
- •2. Замена переменных и интегрирование по частям
- •2.1 Замена переменных:
- •2.2 Интегрирование по частям:
- •3. Интегрирование рациональных дробей
- •4. Универсальная тригонометрическая подстановка
- •5. Интегрирование квадратных рациональных выражений
- •6. Многочлены чебышева некоторые их приложения
- •7. Определенный интеграл. Формула ньютона-лейбница
- •8. Суммы дарбу. Интегрируемость непрерывных функций
- •8.1 Суммы Дарбу:
- •8.2 Интегрируемость непрерывных функций.
- •9. Свойства определенного интеграла
- •10. Численное интегрирование. Метод симпсона
- •Список литературы
СОДЕРЖАНИЕ
Задание………………………………………………………………………………2
Введение…………………………………………………………………………….4
Неопределенный интеграл и его свойства…………………………………7
Замена переменных и интегрирование по частям………………………... 12
Интегрирование рациональных дробей……………………………………17
Универсальная тригонометрическая подстановка……………………….. 21
Интегрирование квадратных иррациональных выражений………………23
Многочлены Чебышева некоторые их приложения……………………...27
Определенный интеграл. Формула Ньютона-Лейбница……………….....31
Суммы Дарбу. Интегрируемость непрерывных функций………………...34
Свойства определенного интеграла………………………………………...40
численное интегрирование. Метод Симпсона…………………………......43
Заключение………………………………………………………………………….46
Список литературы…………………………………………………………………49
ВВЕДЕНИЕ
Мною была выбрана курсовая работа по теме вычисление интегралов, в связи с этим, я решил узнать, откуда появился этот загадочный значок интеграл, почему так называется и такую большую роль играет в математике.
ИНТЕГРАЛ одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.
Символ
![]() введенЛейбницем
(1675 г.). Этот
знак является изменением латинской
буквы S
(первой буквы
слова сумма).
Само слово интеграл
придумал
Я. Бернулли
(1690 г.).
Вероятно, оно происходит от латинского
integero,
которое переводится как приводить
в прежнее состояние, восстанавливать.
(Действительно,
операция интегрирования “восстанавливает”
функцию, дифференцированием которой
получена подынтегральная функция.)
Возможно происхождение слова интеграл
иное: слово integer
означает целый.
введенЛейбницем
(1675 г.). Этот
знак является изменением латинской
буквы S
(первой буквы
слова сумма).
Само слово интеграл
придумал
Я. Бернулли
(1690 г.).
Вероятно, оно происходит от латинского
integero,
которое переводится как приводить
в прежнее состояние, восстанавливать.
(Действительно,
операция интегрирования “восстанавливает”
функцию, дифференцированием которой
получена подынтегральная функция.)
Возможно происхождение слова интеграл
иное: слово integer
означает целый.
В 1696г., появилось название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли.
В современной
литературе множество всех первообразных
для функции f(x)
называется также неопределенным
интегралом.
Это понятие выделил Лейбниц,
который заметил, что все первообразные
функции
отличаются на произвольную постоянную.
А
![]() называютопределенным
интегралом
(обозначение
ввел К. Фурье (1768-1830), но пределы
интегрирования указывал уже Эйлер).
называютопределенным
интегралом
(обозначение
ввел К. Фурье (1768-1830), но пределы
интегрирования указывал уже Эйлер).
Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками древней Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывающий метод, созданный Евдоксом Книдским (ок. 408 - ок. 355 до н. э.) и широко применявшийся Архимедом (ок. 287 - 212 до н. э.).
Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов развития интегрального исчисления. Архимед предвосхитил многие идеи интегрального исчисления. Но потребовалось более полутора тысяч лет, прежде чем эти идеи нашли четкое выражение и были доведены до уровня исчисления.
Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
Строгое изложение теории интеграла появилось только в прошлом веке, Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826 - 1866 гг.), французского математика Г. Дарбу (1842 - 1917).
Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875 - 1941 гг.) и А. Данжуа (1884 - 1974) советским математиком А. Я. Хичиным (1894 -1959 гг.)
Раскрытие темы курсовой работы я провел по следующему плану: Неопределенный интеграл и его свойства; замена переменных и интегрирование по частям; интегрирование рациональных дробей; универсальная тригонометрическая подстановка; интегрирование квадратных иррациональных выражений; многочлены Чебышева некоторые их приложения; определенный интеграл. Формула Ньютона-Лейбница; суммы Дарбу; Интегрируемость непрерывных функций; свойства определенного интеграла численное интегрирование; Метод Симпсона.
1. Неопределенный интеглал и его свойства
Определение.
Если функция F(x)
является первообразной функции f(x),
то выражение F(x)+c
называется неопределенным интегралом
от функции f(x)
и обозначается символом
![]() .
.
Таким образом, по
определению,![]() ,
гдеF′(x)=f(x)
При этом функцию f(x)
называют подынтегральной функцией,
f(x)dx
- подынтегральным
выражением, символ
,
гдеF′(x)=f(x)
При этом функцию f(x)
называют подынтегральной функцией,
f(x)dx
- подынтегральным
выражением, символ
![]() -
знаком интеграла.
-
знаком интеграла.
Следовательно, неопределенный интеграл представляет собой семейство функций y=F(x) +c . Графически он представляет однопараметрическое семейство кривых на плоскости с параметром с.
Например, интеграл
![]() представляет
семейство парабол
представляет
семейство парабол![]() (рис.1)
.
(рис.1)
.
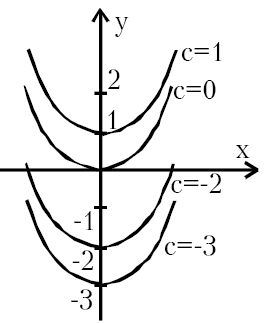
Неопределенный интеграл существует на отрезке [a,b], если
подынтегральная функция непрерывна в каждой точке этого отрезка.
Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.
![]()
Доказательство.
Пусть F′(x)=f(x), тогда
![]() и
и![]()
Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
![]()
Действительно:
![]()
Свойство 3. Неопределенный интеграл от производной функции равен этой функции плюс постоянная с
![]()
Действительно. Найдем следующие производные.
![]()
Так как правые
части равны, то равны и левые, т.е.
![]()
Свойство 4.
![]()
Действительно.
Так как
![]() ,
то результат следует из свойства 3.
,
то результат следует из свойства 3.
Свойство 5. Постоянный множитель можно выносить за знак интеграла, т.е.
![]() a=const
a=const
Свойство 6. Неопределенный интеграл от суммы функций равен сумме интегралов от этих функций, т.е.
![]()
Свойство 7. Свойство инвариантности неопределенного интеграла.
Любая формула интегрирования сохраняет свой вид, если вместо независимой переменной подставить любую дифференцируемую функцию от нее, т.е.
![]() отсюда
следует, что
отсюда
следует, что
![]()
где
![]() -
дифференцируемая функция.
-
дифференцируемая функция.
Доказательство. В силу инвариантности дифференциала первого порядка dF(x)=f(x)dx, поскольку F′(x)=f(x).Кроме того, dF(u)=f(u),где u=φ(x).
Тогда
![]() Свойство доказано.
Свойство доказано.
Следствие 1.
![]()
![]()
Следствие 2.
![]()
![]() aи
b - const
aи
b - const
Пример 1:
![]()
Пример 2:
![]()
Пример 3:
![]()
Пример 4:
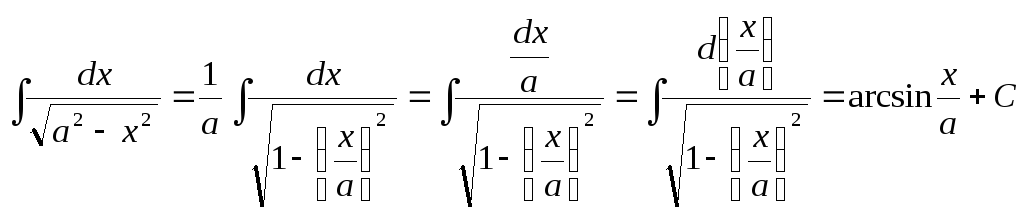
Пример 5:
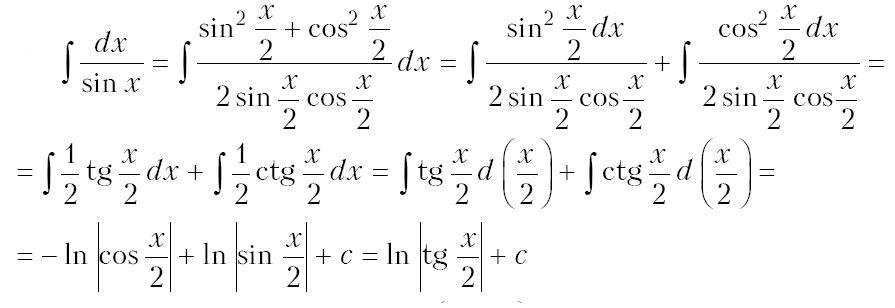
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
1.
![]() (n≠-1).
(n≠-1).
2.
![]() (a
>0, a≠1).
(a
>0, a≠1).
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
![]()
12.
![]()
13.
![]()
14.
![]() (a≠0).
(a≠0).
15.![]() (a≠0).
(a≠0).
16.
![]() (|u|
> |a|).
(|u|
> |a|).
17.
![]() (|u|
< |a|).
(|u|
< |a|).
18.
![]()
19.
![]()
2. Замена переменных и интегрирование по частям
2.1 Замена переменных:
Пусть требуется
найти интеграл
![]() ,
причем непосредственно подобрать
первообразную дляf(x)
мы не сможем , но нам известно, что она
существует.
,
причем непосредственно подобрать
первообразную дляf(x)
мы не сможем , но нам известно, что она
существует.
Сделаем замену переменной в подынтегральном выражении, положив
x=φ(t), (1)
где φ(t)-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx= φ′(t)dt;докажем, что в этом случае имеет место следующее равенство:
![]() (2)
(2)
Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).
Для того чтобы
установить, что выражения, стоящие
справа и слева, одинаковы в указанном
выше смысле, нужно доказать, что их
производные по х равны между собой .
Находим производную от левой части :
![]() Правую
часть равенства (2) будем дифференцировать
по х как сложную функцию, гдеt-промежуточный
аргумент. Зависимость t
от х выражается равенством (1), при этом
Правую
часть равенства (2) будем дифференцировать
по х как сложную функцию, гдеt-промежуточный
аргумент. Зависимость t
от х выражается равенством (1), при этом
![]() и по правилу дифференцирования обратной
функции
и по правилу дифференцирования обратной
функции![]() .
.
Таким образом, имеем
![]()
Следовательно, производные от х от правой и левой частей равенства (2) равны, что и требовалось доказать.
Функцию
![]() следует выбирать так, чтобы можно было
вычислить неопределенный интеграл,
стоящий в правой части равенства (2).
следует выбирать так, чтобы можно было
вычислить неопределенный интеграл,
стоящий в правой части равенства (2).
Замечание. При
интегрировании иногда целесообразнее
подбирать замену переменной не в виде
![]() ,
а в виде
,
а в виде
![]() Проиллюстрируем
это на примере. Пусть нужно вычислить
интеграл, имеющий вид
Проиллюстрируем
это на примере. Пусть нужно вычислить
интеграл, имеющий вид
![]() .
.
Здесь удобно положить
![]() ,
,
тогда
![]()
![]() .
.
Приведем несколько примеров на интегрирование с помощью замены переменных.
Пример 1.
![]() Сделаем
подстановку t=sin
x;
тогда dt=
cosx
dx
и, следовательно,
Сделаем
подстановку t=sin
x;
тогда dt=
cosx
dx
и, следовательно,
![]()
Пример 2.
![]() Полагаем
t=1+x2
;тогда
dt=2xdx
и
Полагаем
t=1+x2
;тогда
dt=2xdx
и
![]()
Пример 3.
![]() Полагаемt=lnx;
тогда
Полагаемt=lnx;
тогда
![]()
![]() .
.
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем какимлибо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения. Этому посвящены большая часть настоящего пункта.
