4. Универсальная тригонометрическая подстановка

Переход в подынтегральной функции к переменной преобразуетR(sin x, cos x) в функцию , рационально зависящую от t;. Выразим sin x, cos x, dx через t: (делим на);(делим на). В результате все компоненты подынтегральной функции выражаются через функции, рационально зависящие отt. Пример 1:

Универсальная тригонометрическая подстановка всегда рационализирует подынтегральную функцию, с её помощью легко берутся интегралы вида(a, b, c - постоянные); однако часто она приводит к очень громоздким рациональным дробям, у которых, в частности, практически невозможно найти корни знаменателя. Поэтому при возможности применяются частные подстановки, которые тоже рационализируют подынтегральную функцию и приводят к менее сложным дробям.

Пример 2:

Воспользуемся универсальной тригонометрической подстановкой:

, ,

Тогда:

Пример 3:

5. Интегрирование квадратных рациональных выражений

5.1 Интегралы вида (m₁, n₁, m₂, n₂, … - целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от х. Они вычисляются подстановкой x=t^s, где s – общий знаменатель дробей ,, … При такой замене переменной все отношения=r₁, =r₂, … являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной t:

5.2 Интегралы вида (m₁, n₁, m₂, n₂, … - целые числа). Эти интегралы подстановкой:

где s – общий знаменатель дробей ,, …, сводятся к рациональной функции от переменнойt.

5.3 Интегралы вида Для вычисления интеграла I₁ выделяется полный квадрат под знаком радикала:

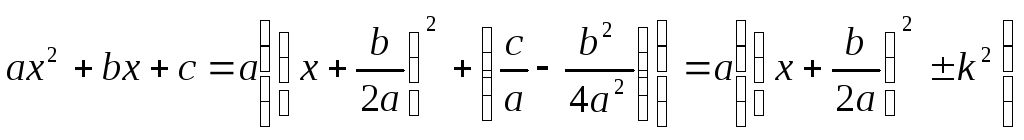
и применяется подстановка:

, dx=du.

В результате этот интеграл сводится к табличному:

В числителе интеграла I₂ выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:

где I₁ – вычисленный выше интеграл.

Вычисление интеграла I₃ сводится к вычислению интеграла I₁ подстановкой:

5.4 Интеграл вида Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.

Квадратный трехчлен ax²+bx+c путем выделения полного квадрата и замены переменной может быть представлен в виде Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:

Интеграл подстановкой

u=ksint (или u=kcost)

сводится к интегралу от рациональной функции относительно sint и cost.

5.5 Интегралы вида (m, n, p є Q, a, b є R). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома , выражаются через элементарные функции только в следующих трех случаях:

• если p є Z, то применяется подстановка:

x=t^s,

где s – общий знаменатель дробей m и n;

• если Z, то используется подстановка:

a+bxⁿ=t^s,

где s – знаменатель дроби

• если 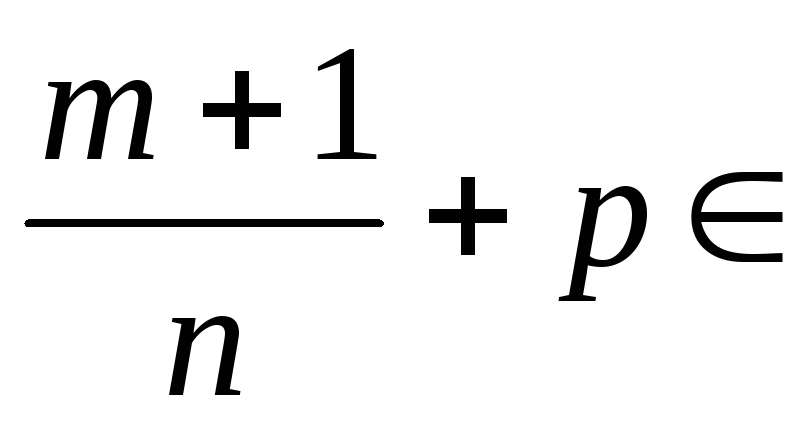Z, то применяется подстановка:

ax^-n+b=t^s,

где s – знаменатель дроби

Пример1: Это интеграл типаI. Подстановка x=a sin t.