2.3. Уравнение д. Бернулли для элементарной струйки идеальной жидкости

Выше были получены дифференциальные уравнения движения идеальной жидкости и уравнение неразрывности движения, образующие замкнутую систему уравнений. Для решения конкретных инженерных задач необходимо уметь находить интегралы этих уравнений. Методы решения дифференциальных уравнений в частных производных (так называемые уравнения математической физики) приводятся в соответствующих разделах высшей математики. Сразу же оговоримся, что рассматриваемая система уравнений настолько сложа, что до настоящего времени еще не получено ее решение в общем виде. Однако для некоторых частных случаев движения жидкости решение этих уравнений может быть получено. В частности, эта система сможет быть проинтегрирована, если рассматривать установившиеся движение идеальной жидкости вдоль линии тока (или в элементарной струйке).

Проанализируем, как упростятся уравнения Л. Эйлера в случае установившегося движения жидкости. Правые части этих уравнений ;ипредставляют собой проекции ускорений движения жидкой частицы на оси х, у иz и являются полными производными по времени от соответствующих проекций скорости ее движения на те же оси.

В случае установившегося движения жидкости скорость и ее проекции есть функции лишь координат и не зависят от времени. Это означает, что частные производные от скорости и ее проекций повремени равны нулю: .

Тогда полные производные примут вид:

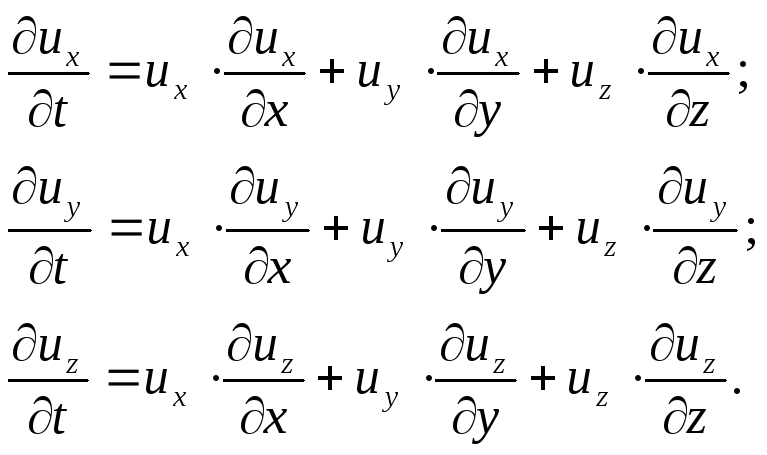
Это обстоятельство мы будем иметь в виду при дальнейших выкладках. Прежде чем перейти к интегрированию уравнений движения идеальной жидкости, примем следующие дополнительные условия:

1. из внешних массовых сил действует лишь сила тяжести;

2. гидродинамическое давление является функцией координат и не зависит от времени;

3. жидкость является несжимаемой ().

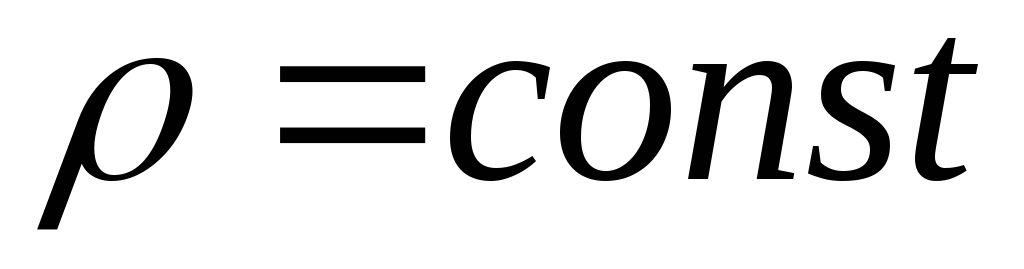Умножим уравнения Л.Эйлера соответственно на ,ии почленно сложим. При этом будем считать, что,иявляются проекциями на координатные оси бесконечно малого участка пути, пройденного частицей жидкости за времявдоль линии тока (или траектории, так как мы рассматриваем установившееся движение, при котором линии тока и траектории движения совпадают). Осьz направим вертикально вверх.

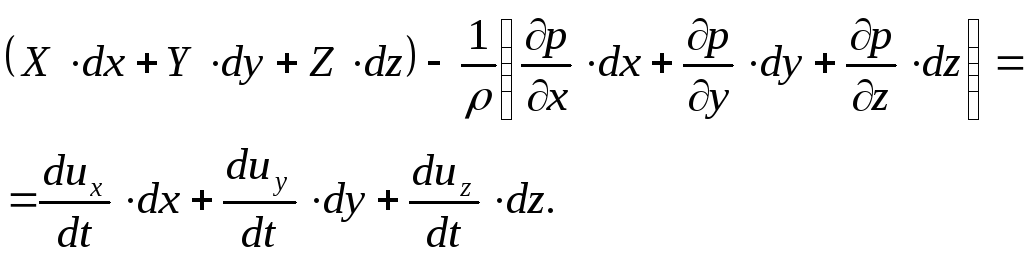(11.10)

Проекции единичной массовой силы (в данном случае силы тяжести) примут следующие значения при выбранном направлении осей координат:

; ;.

Поэтому первый трехчлен в выражении (11.10) будет равен - .

Второй трехчлен при принятом условии независимости гидродинамического давления от времени, как легко видеть, представляет собой полный дифференциал давления:

.

Трехчлен в правой части выражения (11.10) преобразуем следующим образом:

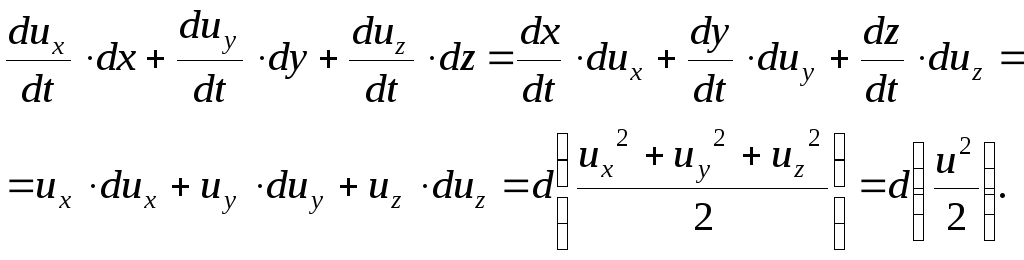
Следовательно, при установившемся движении этот трехчлен представляет собой полный дифференциал от половины квадрата скорости движения частицы вдоль линии тока.

С учетом всего изложенного перепишем уравнение (11.10),

,

или

.

Деля на g и учитывая, что , получим:

.

Интегрируя это дифференциальное уравнение в полных дифференциалах, придем к следующему результату:

(11.11)

Это уравнение называется уравнением Д.Бернулли, оно справедливо при установившемся движении идеальной жидкости и означает, что сумма трех входящих в него величин есть величина постоянная для данной линии тока (траектории). Особо подчеркиваем, что для всякой иной линии тока (траектории) значение этой постоянной может быть другим.

Пусть в сечении 1-1 элементарной струйки площадь ее живого сечения равна , движения жидкости в этом сечении, а гидродинамическое давление в этом сечении равно. Соответствующие величины для живого сечения этой же струйки 2-2 обозначим,и(рис.II.00).

Превышение центров тяжести площадей живых сечений 1-1 и 2-2 над произвольно выбранной горизонтальной плоскостью сравнения обозначим и.

Масса жидкости, прошедшей за время через сечение 1-1, привносит с собой в отсек элементарной струйки 1-1 и 2-2 кинетическую энергию в размере:

.

Эта же масса жидкости обладает и запасом потенциальной энергии, равной:

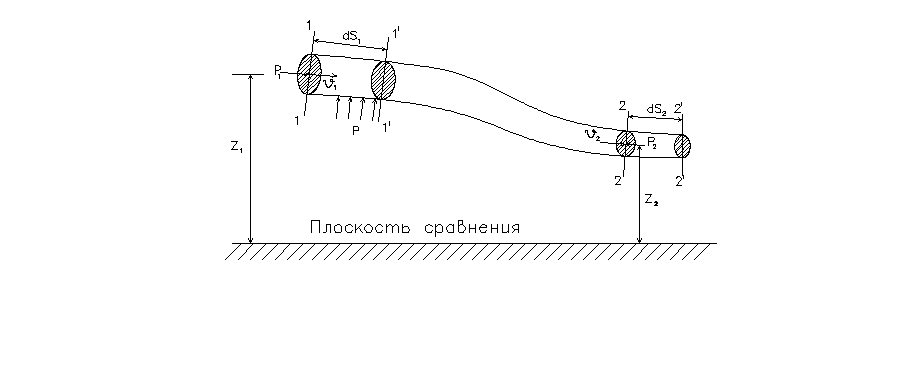
Рис. II.00

Таким образом, через сечение 1-1 за время жидкостью привносится энергия, равная сумме перечисленных видов энергий:

Аналогично получим, что энергии, выносимая жидкостью за это же время через сечение 2-2, будет равна:

Применяя закон сохранения энергии к рассматриваемому случаю, можем утверждать, что энергия, внесенная жидкостью за время в отсек элементарной струйки, должна быть равна энергии, вынесенной жидкостью из этого же отсека за то же время, т.е.или

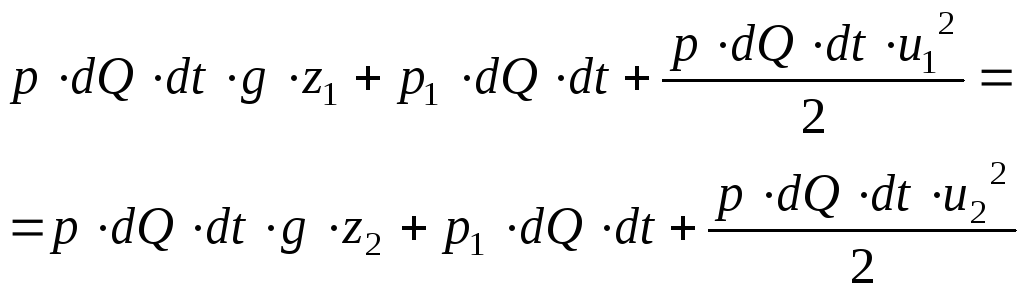
Отнесем полученное равенство вносимых и выносимых жидкостью полных энергией к единице веса жидкости, для чего поделим полученное выражение на , помня, что. В результате получим:

(11.12)

Это и есть уравнение Д.Бернулли.

Энергию, приходящуюся на каждую единицу веса жидкости, впредь будем называть удельной энергией и обозначать . Тогда уравнение (11.12) можно переписать в виде:

. (11.13)