3. Двумерное нормальное распределение

Среди законов распределения двумерной с.в. чаще всего на практике встречается нормальное (гауссово) распределение вероятностей.

Нормальным законом распределения на плоскости называют распределение вероятностей двумерной случайной величины (X, Y), если её функция плотности распределения задаётся равенством

(15) ,

где и - параметры данного распределения. Итак, нормальный закон на плоскостиопределяется пятью параметрами: и .Обычно ихназывают параметрами распределения.

Можно доказать, что эти параметры имеют следующий вероятностный смысл: – математические ожидания, - средние квадратичные отклонения, – коэффициент корреляции с.в. , причём так определённая функцияявляется функцией плотности двумерного распределения вероятностей с.в.т.е. имеет место равенство:

(16) (Контроль).

Это значит, что двумерное нормальное распределение полностью определяется заданием его числовых характеристик, что очень удобно на практике. Обычно на практике опытным путём эти параметры находятся и получают совместную плотность двух нормально распределённых с.в.и. Докажем следующее утверждение.

Теорема 12.5. Для функции определённой равенством (15) плотность вероятностей одномерных с.в. исправедливы равенства:

(17) ;

(18) .

Доказательство. Покажем первое из них. Согласно свойству 5, функции плотности (см. первую формулу (14) п.11.6.) имеет место равенство

=

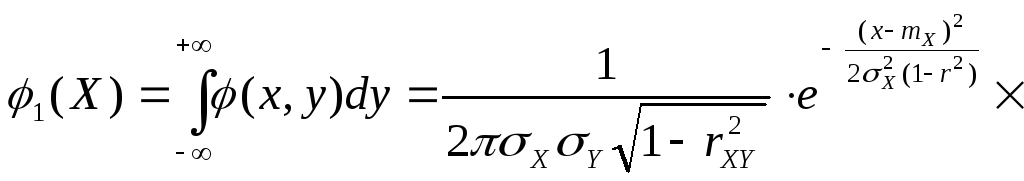
C учётом интеграла Пуассона: , упростив (используя значениясогласно формулам (13) и (10) последней замены, получим равенство (17), т.е.

.

Аналогично получается равенство (18).

Тем самым показано, что и. График плотностинормального распределения у двумерной случайной величиныкак уже было упомянуто ранее (см. рис.42) представляет холмообразную поверхность, вершина которой находится в точке, т.е. максимальное значение функциидостигается в точке ().

Сечения поверхности распределения плоскостями, проходящими через точку перпендикулярно плоскости, изображают кривые Гаусса вида.

Пересекая поверхность распределения плоскостьюпараллельной плоскости, получим в сечении эллипс, уравнении проекции которого на плоскость, имеет вид

(19) ,

где . (В силу ограничения нааргумент логарифма меньше 1, следовательно, значение логарифма отрицательно). Если в равенстве (19) осуществить традиционное преобразование параллельного переноса и поворота осей координат по известным формулам (из курса аналитической геометрии)

где угол определяется равенством, то уравнение (19) приводится к каноническому уравнению эллипса. Эллипс (19) называетсяэллипсом рассеяния; оси симметрии эллипса (они образуют с осьюуглы) – называютсяглавными осями рассеяния, а центр эллипса - называютцентром рассеяния.

Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Действительно, пусть и некоррелированны. Тогда, полагая в формуле (17), получим

(20) .

Отсюда (с учётом формул (17) и (18)) легко следует равенство . Для этого случая (некоррелированных с.в.) уравнение эллипса (19) принимает вид:

Этот эллипс при имеет вид:

(рис.44)

Задание.Начертите эллипс при .

Следовательно, если составляющие нормально распределенной случайной величины некоррелированны, то функция плотности двумерного распределения равна произведению соответствующих функций плотностей составляющих, а отсюда и следует независимость составляющих. Справедливо и обратное утверждение.

Итак, для нормально распределённых с.в. на плоскости термины «независимость» и «некоррелированность» являются эквивалентными.

Замечание.В частности, если, то распределение (20) называетсякруговыми в этом случае имеет вид:

Написанное выражение, обладает круговой симметрией по отношению к точке .

Следствие. Если с.в. инезависимы, то вероятность попадания двумерной с.в. ,распределённый по нормальному закону в области , вычисляется по формуле:

,

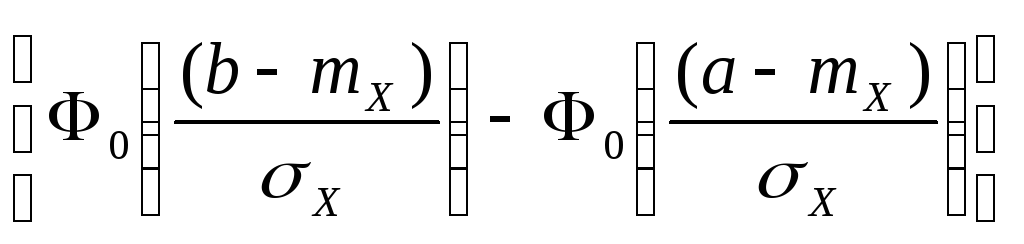где функция Лапласа.

Доказательство непосредственно выводится на основании формулы законов распределения вероятностей независимых с. в. ис последующим применением равенства.

В общем случае, так как произвольную область можно приближённо заменить областью составленный из прямоугольников, то на этом основывается применение так называемых «сеток рассеивания».

Можно также показать, что вероятность попадания случайной точки в один из эллипсов рассеяния равна

Пример 3. Орудие обстреливает плоскость Цель находится в начале координат. Как известно, в реальных условиях стрельбы точка попадания снаряда не совпадаетабсолютно точно с целью: при стрельбе неизбежны отклонения. Отклонения вызываются целым рядом причин: неточностью установки прицела, переменчивостью атмосферных условий, неравномерностью горения заряда и т.д. В теории стрельбы исходят из предположения, что точка попадания распределена по нормальному закону (причем центр распределения совпадает, разумеется, с местом положения цели). Основанием для такого предположения является множественность причин, вызывающих отклонения, и незначительность действия каждой из них в отдельности. Примем, что в данном случае распределение точки попадания является круговым нормальным распределением с центром в начале координат, т. е. что плотность распределения имеет вид:

.

Поскольку точка попадания является случайной точкой, ее расстояние до начала координат будет случайной величиной.

Требуется найти для этой величины закон распределения.

Решение. Обозначим указанное расстояние через . Вероятность событияравна интегралу от функции по области, заключенной между концентрическими окружностямии. Переходя в этом интеграле от прямоугольных координатк полярным, будем иметь:

.

Отсюда видно, что плотность вероятности случайной величины есть функция

.

Пример 4. Производится ряд независимых «выстрелов» по плоскости . Рассеивание точек попадания то же, что и в предыдущем примере. Как много следует сделать выстрелов, чтобы с вероятностьюпопасть хотя бы раз в цель, имеющую вид круга радиусас центром в начале координат?

Решение. Если производится один выстрел, то вероятность не попасть в указанный круг равна:

.

Если производится независимых выстрелов, то вероятностьне попасть ни разу в указанный круг равна . Следовательно, вероятность хотя бы одного попадания привыстрелах будет. Для того, чтобы выполнялось неравенство

или

,

нужно взять

Пример 5. Найти вероятность попадания точки в прямоугольник,если плотность совместного распределения с.в.иравна

Решение. Функцию перепишем в виде

где мы воспользовались равенствами:

.

Следовательно, с.в. иявляются независимыми и.Поэтому (с учётом равенство (38) пункта 9.9. и таблицы значения функции Лапласа) имеем