5. Плотность совместного распределения вероятностей

двумерной непрерывной случайной величины

Основной характеристикой непрерывной двумерной случайной величины является её плотность вероятности. Мы задавали двумерную дискретную случайную величину при помощи интегральной функции. Непрерывную двумерную величину можно также задать, пользуясь дифференциальной функцией распределения. Здесь и далее мы будем предполагать, что интегральная функция всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную смешанную частную производную второго порядка.

Дифференциальной функцией распределения двумерной непрерывной случайной величины называют вторую смешанную частную производную от функции:

(9) .

Другими словами, плотностью распределения вероятностей (или совместной плотностью) непрерывной двумерной с.в. называется вторая смешанная производная её функции распределения. Плотность системы двух непрерывных случайных величинесть предел отношения вероятности попадания случайной точкив элементарный прямоугольник со сторонамии, примыкающий к площади этого прямоугольника, когда его размерыистремятся к нулю

(рис.41 из Письменного)

Действительно, используя равенства (5), получаем: средняя плотность вероятности в данном прямоугольнике равна

Переходя к пределу в этом равенстве, при иполучаем

Следовательно, равенство (9) получено

=.

Таким образом, по аналогии с плотностью вероятности одномерной непрерывной с.в., для двумерной случайной величины плотность вероятности определяется как функция,удовлетворяющая условию:

(10)

Выражение называетсяэлементом вероятностидвумерной случайной величины .

Пример 5. Найти дифференциальную функцию системы случайных величин по известной интегральной функции

Решение. По определению дифференциальной функции системы случайных величин

найдем частную производную по x от интегральной функции

;

Берём от полученного результата частную производную по y, в итоге получим искомую дифференциальную функцию

=,

где.

Геометрически эту функцию можно истолковать на в пространстве как некоторую поверхность, которую называютповерхностью распределения вероятностей системы двух н.с.в.

Рис. 42 из Письм.

Свойства плотность распределения двумерной с.в.

1. Плотность распределения двумерной случайной величины неотрицательна, т.е.

.

Это свойство следует из того, что является неубывающей функцией по каждому из аргументов.

2. Вероятность попадания двумерной с.в. в заданную областьравна двойному интегралу от плотности по областит.е.

(11) .

Действительно, элемент вероятности (см. (10)) представляет собой вероятность попадания случайной точкив прямоугольник со сторонамии(с точностью до бесконечно малых более высокого порядка по сравнению с). Далее, разобьём областьна прямоугольники и применив к каждому из них равенство (10), по теореме сложения вероятностей, при стремлении к нулю площадей прямоугольников (т.е.и), получаем формулу (11).

Геометрически эта вероятность изображается объёмом цилиндрического тела, ограниченного сверху поверхностью распределения и опирающегося на область.

3. Функция распределения двумерной случайной величины может быть выражена через её плотность распределения по формуле

(12) .

Используя формулу (8) (область есть прямоугольник, ограниченный абциссамии ординатами), выражаем функцию распределениясистемы случайных величинчерез плотность

.

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятностей двумерной случайной величины равен единице, т.е.

(13) (условие нормировки).

Положив в равенстве (9) непосредственно получим (13). Геометрически свойство4 означает, что «объём тела, ограниченного поверхностью распределения и плоскостью равен единице».

5. Плотность распределения одномерных составляющих имогут быть найдены по формулам:

(14)

Действительно, найдём сначала функции распределения (зная совместную плотность распределения с.в. ), составляющихи:

(15)

(16)

Дифференцируя первое равенство (14) относительно а второе равенство (14) относительнополучим соответственно плотности распределения с.в.и:

(17)

(18)

Итак, плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, при этом переменная интегрирования соответствует другой составляющей.

Пример 6. Двумерная случайная величина задана функцией плотности вероятности

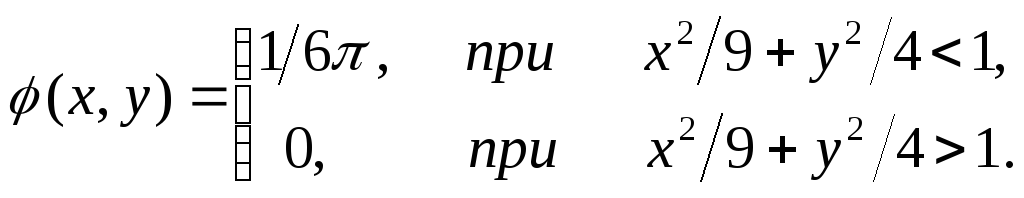
Найти дифференциальные функции составляющих X и Y.

Решение. Найдем дифференциальную функцию составляющей X по формуле (17)

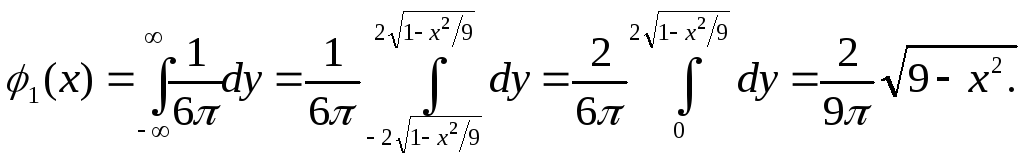
Следовательно,

Аналогично, пользуясь формулой (18), найдем дифференциальную функцию составляющей Y:

(Убедится самостоятельно!)

Задание. Самостоятельно убедитесь в том, что найденные функции удовлетворяют соотношениям:

и

Замечание. Отметим, чтов общем случае решение обратной задачи: «восстановить закон распределения системы случайных величин по известным законам распределения составляющих системы» невозможно.