2. Корреляционный момент, коэффициент корреляции

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих пользуются и другими характеристиками, к числу которых относятся корреляционный моментикоэффициент корреляции(кратко было упомянуто в конце Т.8.п.8.6).

Корреляционным моментом (иликовариацией, или моментом связи) двух случайных величинX иY называется м. о. произведения отклонений этих величин (см. равенство (5) п. 8.6):

(7) .

Следствие 1. Для корреляционного момента с.в. X иYтакже справедливы равенства:

,

где соответствующие централизованные с.в.X иY (см. п.8.6.).

При этом: если - двумерная д.с.в., то ковариация вычисляется по формуле

(8) ;

если - двумерная н.с.в., то ковариация вычисляется по формуле

(9)

Формулы (8) и (9) получены на основании формул (6) п.12.1. Имеет место вычислительная формула

(10)

которая выводится из определения (9) и на основании свойств м.о., действительно,

.

Следовательно, формул (36) и (37) можно переписать в виде

(11) ;

Корреляционный момент служит для характеристики связи между величинами X иY.

Как будет показано ниже, корреляционный момент равен нулю, если XиY являются независимыми;

Следовательно, если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.

Теорема12.1. Корреляционный момент двух независимых случайных величин X иY равен нулю, т.е. для независимых с.в. X иY,

Доказательство.Так какX иYнезависимые случайные величины, то их отклонения

и

также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых с. в. равно произведению математических ожиданий сомножителей,, поэтому

.

Замечание. Из этой теоремы следует, что если то с.в. X иY зависимы и в таких случаях с.в. X иYназываюткоррелированными. Однако из того, что не следует независимость с.в.X иY.

В этом случае (с.в.X иYназываютнекоррелированными, тем самым из независимости вытекаетнекоррелированность; обратное утверждение, вообще говоря, неверно (см. далее пример 2.)

Рассмотрим основные свойства корреляционного момента.

Cвойства ковариации:

1.Ковариация симметрична, т.е. .

Непосредственно следует из формулы (38).

2. Имеют место равенства:т.е. дисперсия с.в. является ковариацией её с самой собой.

Эти равенства прямо следуют из определения дисперсии и равенство (38) соответственно при

3. Справедливы равенства:

Эти равенства выводятся из определения дисперсии, ковариации с.в.и, свойств 2.

По определению дисперсии (с учётом централизованности с.в. ) мы имеем

теперь, на основании (33) и свойств 2 и 3, получим первое (со знаком плюс) свойство 3.

Аналогично, вторая часть свойства3, выводится из равенство

.

4. Пустьпостоянные числа,тогда справедливы равенства:

Обычно эти свойства называются свойствами однородностью первого порядка и периодичностью по аргументам.

Докажем первое равенство, при этом будем использовать свойства м.о. .

.

Теорема 12.2. Абсолютное значение корреляционного момента двух произвольных случайных величин X и Y не превышает среднего геометрического их дисперсий: т.е.

(12)

Доказательство. Заметим, что для независимых с.в. неравенство выполняется (с.м. теорему 12.1.). Итак, пусть с.в.X и Y зависимые. Рассмотрим стандартные с.в.ии вычислим дисперсию с.в.с учётом свойства 3, имеем: с одной стороныС другой стороны

Следовательно, с учётом того, что и- нормированные (стандартизированные) с.в., то для них м.о. равна нулю, а дисперсия равна 1, поэтому, пользуясь свойством м.о.получим

а следовательно, на основании того, что получим

Отсюда следует, что т.е.

=

Утверждение доказано.

Из определения и свойства ковариации следует, что она характеризует и степень зависимости с.в., и их рассеяния вокруг точки Размерность ковариации равна произведению размерностей случайных величинXиY. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величинXиY, величина корреляционного момента будет иметь различные значения в зависимости от того, в каких единицах были измерены величины.

Пусть, например, X и Y были измерены в сантиметрах и ; если измерить XиY в миллиметрах, тоЭта особенность корреляционного момента и есть недостатком этой числовой характеристики, так как сравнение корреляционных моментов различных систем случайных величин становится затруднительным.

Для того чтобы устранить этот недостаток, вводят новую числовую характеристику- - «коэффициент корреляции».

Коэффициентом корреляции случайных величин иназывают отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

(13) .

Так как размерность равна произведению размерностей величин и,имеет размерность величиныσ_yимеет размерность величины, то есть просто число (т.е. «безразмерная величина»). Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения с.в., в этом состоитпреимуществокоэффициента корреляции перед корреляционным моментом.

В Т.8. п.8.3 нами было введено понятие нормированной с.в., формула (18), и доказана теорема о том, чтои(см. там же теорема 8.2.). Здесь докажем следующее утверждение.

Теорема 12.3. Длялюбых двух случайных величин и справедливо равенство.Другими словами, коэффициент корреляции любых двух с.в.X иYравно корреляционному моменту их соответствующих нормированныхс.в.и .

Доказательство. По определению нормированных случайных величини

и.

Учитывая свойство математического ожидания: и равенство (40) получим

Утверждение доказано.

Рассмотрим некоторые часто встречающие свойства коэффициента корреляции.

Свойства коэффициента корреляции:

1. Коэффициент корреляции по абсолютной величине непревосходит 1, т.е.

Это свойство прямо следует из формулы (41) - определения коффициента корреляции и теоремы 13.5. ( см. равенство (40)).

2. Если случайные величиныинезависимы, токоэффициент корреляции равен нулю, т.е. .

Это свойство является прямым следствием равенства (40) и теоремы 13.4.

Следующее свойство сформулируем в виде отдельной теоремы.

Теорема 12.4.

Если с.в.имежду собой связаны линейной функциональной зависимостью, т.е.то при этом

и наоборот, если ,то с.в.и между собой связаны линейной функциональной зависимостью, т.е. существуют постоянныеи такие, что имеет место равенство

Доказательство. Пусть тогда на основании свойства 4 ковариации, имеем

и поскольку, , поэтому

Следовательно, . Равенство в одну сторону получено. Пусть далее,, тогда

следует рассматривать два случая:1) и 2)Итак, рассмотрим первый случай. Тогда по определениюи следовательно из равенства, где. В нашем случае, поэтому из равенства (см. доказательство теоремы 13.5.)

=,

получаем, что , значитпостоянна. Так каки поскольку, тодействительно,

.

Следовательно,

.

Аналогично, показывается, что для имеет место (проверьте самостоятельно!)

,.

Некоторые выводы:

1. Если инезависимыес.в., то

2. Если с.в.имежду собой связаны линейно, то.

3. В остальных случаях :

В этом случае говорят, что с.в.исвязаны между собойположительной корреляцией, еслив случаях жеотрицательной корреляцией. Чем ближек единице, тем больше оснований считать, чтос.в.исвязаны линейной зависимостью.

Отметим, что корреляционные моменты и дисперсии системы с.в. обычно задаются корреляционной матрицей:

.

Очевидно, что определитель корреляционной матрицы удовлетворяет:

.

Как уже было отмечено, если две случайные величины зависимы, то они могут быть как коррелированными, так инекоррелированными.Другими словами, корреляционный момент двух зависимых величин может бытьне равен нулю, но может иравняться нулю.

Пример 1. Закон распределения дискретной с.в.задан таблицей

	-1	0	1
0
1

Найти коэффициент корреляции

Решение. Находим законы распределения составляющихи:

Теперь вычислим м.о. составляющих:

.

Этих величин можно было находить на основании таблицы распределения с.в.

из равенства (1) пункта 12.1. Например,

.

Аналогично, находите самостоятельно.

Вычислим дисперсии составляющих при это будем пользоваться вычислительной формулой:

Следовательно,Далее, на основании первой формулы

(6) имеем:

Составим закон распределения , а затем найдём:

При составлении таблицы закона распределения следует выполнять действия:

1) оставить лишь различные значения всевозможных произведений .

2) для определения вероятности данного значения , нужно

складывать все соответствующие вероятности, находящиеся на пересечении основной таблицы, благоприятствующие наступлению данного значения.

В нашем примере с.в.принимает всего три различных значения. Здесь первое значение () соответствует произведениюиз второй строки ииз первого столбца, поэтому на их пересечении находится вероятностное числоаналогично

,

которое получено из суммы вероятностей, находящихся на пересечениях соответственно первой строки и первого столбца (0,15 ; 0,40; 0,05) и одно значение , которое находится на пересечении второй строки и второго столбца, и наконец,, которое находится на пересечении второй строки и третьего столбца.

Из нашей таблицы находим:

Находим корреляционный момент, используя формулу (38):

Находим коэффициент корреляции по формуле (41)

Таким образом, отрицательная корреляция.

Упражнение.Закон распределения дискретной с.в. задан таблицей

	-1	0,5	1
0,2
1

Найти коэффициент корреляции

Рассмотрим пример, где окажется две зависимые случайные величинымогут бытьнекоррелированными.

Пример 2. Двумерная случайная величина )задана функцией плотностью

Докажем, что и зависимые,нонекоррелированные случайные величины.

Решение.Воспользуемся ранее вычисленными плотностями распределения составляющихи :

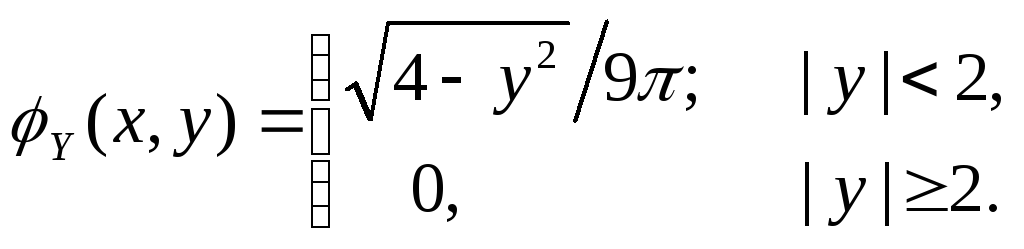
Так как ,то изависимые величины. Для того, чтобы доказать некоррелированность и, достаточно убедиться в том, что

Найдем корреляционный момент по формуле:

Поскольку дифференциальная функция симметрична относительно оси OY, то аналогично, в силу симметрии относительно оси OX. Поэтому, вынося постоянный множитель

Внутренний интеграл равен нулю (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала координат), следовательно, , т.е. зависимые случайные величиныи между собой некоррелируют.

Итак, из коррелированности двух случайных величин следует их зависимость, но из некоррелированности ещё нельзя заключить о независимости этих величин.

Однако, для нормально распределённых с.в. такой вывод является исключением, т.е. из некоррелированности нормально распределенных с.в. вытекает их независимость.

Этому вопросу посвящается следующий пункт.