9. Условные законы распределения составляющих

системы непрерывных случайных величин

Пусть непрерывные случайные величины иобразуют непрерывную двумерную случайную величину зависимую системус плотностью, аи-плотности распределения соответственно с.в.и с.в..

Условной дифференциальной функцией (или условная вероятность) составляющей при данном значении называют отношение дифференциальной функции системы к дифференциальной функциисоставляющей с.в. :

(26) .

Если известна плотность распределения вероятности (дифференциальная функция), топо второй формуле (14) пункта 11.6. получим

(27)

при этом условная плотность обладает свойствами плотности распределения, так например: или, и т.д.

Подчеркнем, что отличие условной функции плотности от безусловной функции состоит в том, что дает распределениепри условии, что составляющая приняла значение ; функция жедаёт распределениенезависимо от того, какие из возможных значений приняла составляющая.

Аналогично определяется условная плотность распределения составляющей при данном значении

(28)

(29)

Запишем формулы (26) и (28) в виде

(30)

Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.

Равенство (30) называют правилом (теоремой) умножения плотностей распределений (она аналогична теореме умножения вероятностей для событий).

Пример 14. Двумерная случайная величина задана дифференциальной функцией

Найти условные дифференциальные законы распределения вероятностей с.в. и.

Решение. Найдем условную дифференциальную функцию составляющей X при по формуле (23):

Так как приx²+ y²>r², то φ(x|y)=0 при.

Пользуясь формулой (25), аналогично найдем условную дифференциальную функцию составляющей Y:

Задание. Самостоятельно убедитесь в том, что найденные функции удовлетворяют соотношениям:

и

Пример 15. Двумерная с.в. задана плотностью совместного распределения

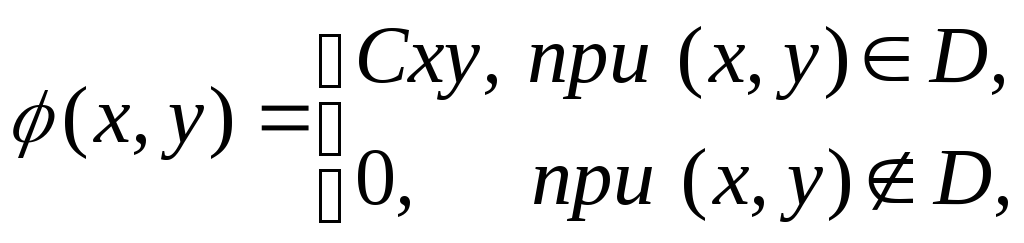
гдеобласть на плоскости

Найти безусловное и условное распределение составляющей Убедится, что случайные величиныизависимы.

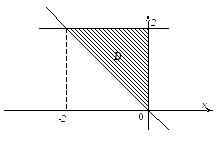
Рис. 43.(Письменный)

Решение. Сначала найдём коэффициент из условия нормировки:

Следовательно, Теперь находим

т.е. . Проверим контроль:

Для нахождения воспользуемся формулой (23) предварительно найдя

Тогда

Проверим контроль:

Как видно, безусловный закон распределения с.в. функцияне совпадает с условным законом распределения случайной величиныс. Значит случайные величины изависимы.

Тема12. Числовые характеристики двумерной случайной величины

1. Математическое ожидание и дисперсия

Для системы случайных величин также вводятся числовые характеристики по аналогию одномерных с.в. (см. Тема 8). В качестве числовых характеристик системы обычно рассматривают моменты различных порядков (см. Тема 8, п. 8.6 - 8.8). На практике часто используются моменты I иIIпорядков, т.е. математическое ожидание (коротко м.о.), дисперсия и корреляционный момент двумерной случайной величины.

М.о. и дисперсия двумерной с.в. служат соответственно средним значением и мерой рассеивания значений системы случайной величины. Корреляционный момент выражает меру взаимного влияния с.в., входящих в систему .

Математическим ожиданием двумерной с.в.называется совокупность двух м.о.иопределяемых равенствами:

(1)

если - дискретная система с.в., гдеи

(2) ,

если - непрерывная система с.в., гдеплотность распределения системы.

Дисперсией двумерной системы с.в. называется совокупность двух дисперсийиопределяемых соответственно равенствами:

(3)

если - дискретная система с.в., и

(4)

если - непрерывная система с.в., гдеплотность распределения системы.

Дисперсия иуказывают на меру рассеивания (разброса) с.в. точкив направлении осей координат ив окрестности точки центра разбросана плоскости.

Математические ожидания иявляются частными случаями начального момента(для одномерных с.в. см. Т. 8 п.8.6) совместного порядкасистемы с.в., определяемого равенством, в частности,;

.

Дисперсия иявляются частными случаями центрального момента(для одномерных с.в. см. Т. 8 п.8.6) совместного порядкасистемы с.в., определяемого равенством, в частности,

;.

Математическое ожидание с.в. , являющейся функцией компонентидвумерной с.в.находится, (соответствующие д.с.в. и н.с.в.), по формулам:

(5) ;

Начальный момент второго порядка часто встречается в приложениях,

Они вычисляются по формулам (соответствующие д.с.в. и н. с.в.)

(6) ;