6.2. Элементарные переключательные (логические) функции двух переменных

Рассмотрим все функции двух переменных (табл. 25).

Таблица 25

Переключательные функции двух переменных

		2^0	2^1	2^2	2^3
		Набор				Название	Формула
2^0	х1	0	1	0	1	функции
2^1	х2	0	0	1	1
	f0	0	0	0	0	Константа 0	0
	f1	1	0	0	0	Функция Пирса (Вебба), «стрелка Пирса», ИЛИ-НЕ	х1х2=
	f2	0	1	0	0	Запрет х2
	f3	1	1	0	0	Отрицание х2
	f4	0	0	1	0	Запрет х1
	f5	1	0	1	0	Отрицание х1
	f6	0	1	1	0	Сложение (сумма) по mod2	х1х2=
	f7	1	1	1	0	Функция Шеффера, «штрих Шеффера», И-НЕ	х1|х2=
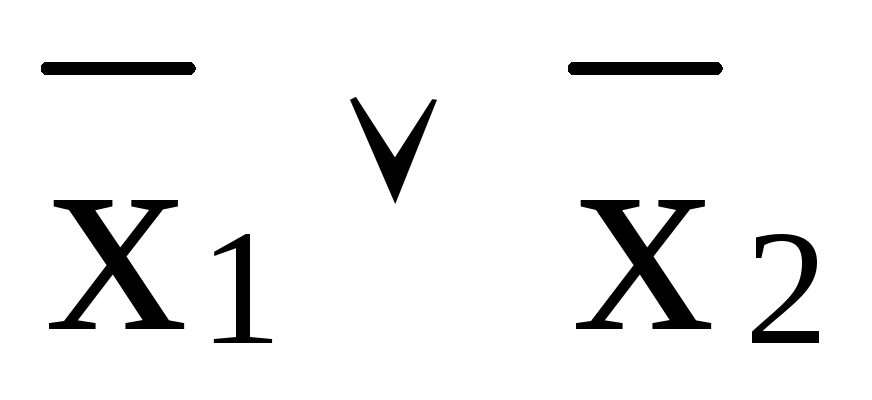
	f8	0	0	0	1	Конъюнкция, И	х1х2
	f9	1	0	0	1	Эквиваленция (эквивалентность)	х1х2=
	f10	0	1	0	1	Повторение х1	х1
	f11	1	1	0	1	Импликация х2 в х1	х2х1
	f12	0	0	1	1	Повторение х2	х2
	f13	1	0	1	1	Импликация х1 в х2	х1х2
	f14	0	1	1	1	Дизъюнкция, ИЛИ	х1х2
	f15	1	1	1	1	Константа 1	1

Всего таких функций имеется 2²²=2⁴=16. Есть функции, зависящие только от одной переменной. Есть функции, не зависящие от переменных, – константы 0, 1. Такие функции называют вырожденными:

f₃(x₁x₂)=;f₅(x₁x₂)=;f₁₀(x₁x₂)=х₁; f₁₂(x₁x₂)=х₂;

f₀(x₁x₂)=0; f₁₅(x₁x₂)=1.

Некоторые функции мы тоже уже знаем: конъюнкцию f₈(x₁x₂)=х₁х₂ (точку между х₁ и х₂ опускаем); эквиваленцию (эквивалентность) f₉(x₁x₂)=х₁х₂=х₁х₂(здесь эквиваленция представлена в виде дизъюнкции двух конъюнкций, что можно доказать, составив таблицу истинности); импликациюf₁₁(x₁x₂)=х₂х₁=х₁, f₁₃(x₁x₂)=х₁х₂=х₂; дизъюнкцию f₁₄(x₁x₂)=х₁х₂.

Кроме этого, имеются другие функции, зависящие от двух переменных: f₁(x₁x₂)=– функция Пирса (Вебба) («стрелка Пирса»);f₂(x₁x₂)=– запрет х₂; f₄(x₁x₂)=– запрет х₁; f₆(x₁x₂)=x₁x₂ –сложение по модулю 2 (функция, инверсная эквиваленции); f₇(x₁x₂)=– функция Шеффера («штрих Шеффера»).

6.3. Функциональная полнота систем переключательных функций

Элементарные переключательные функции позволяют получить сложные функции от большего числа аргументов путем подстановки в данную функцию вместо ее переменных других функций. Такой метод получения функций называется суперпозицией. Например, имея элементарные функции двух переменных z₁=x₁x₂ и z₂=x₃x₄ можно получить функции z₃=х₁(x₃x₄), z₄=x₃х₁x₂, зависящие от трех переменных.

При использовании суперпозиции возникает следующая проблема, – каким должен быть минимальный состав элементарных логических функций, который позволяет путем их суперпозиции получить любую сколь угодно сложную логическую функцию от конечного числа переменных.

Эта проблема называется проблемой функциональной полноты переключательных функций. Для ее решения были выделены следующие классы логических функций:

1) класс функций, сохраняющих константу 0. В этот класс входят функции, которые на нулевом наборе переменных принимают нулевое значение: f(00...0)=0. Такова, например, конъюнкция f₈(00)=00=0;

2) класс функций, сохраняющих константу 1. В этот класс входят функции, которые на единичном наборе переменных принимают единичное значение: f(11...1)=1. Этим свойством также обладает конъюнкция f₈(11)=11=1. Классы 1, 2 легко устанавливаются по таблице истинности;

3) класс самодвойственных функций. Переключательные (логические) функции f(х₁х₂...х_n) и g(х₁х₂...х_n) называются двойственными, если имеет место равенство f(х₁х₂...х_n)=, т.е. если одна функция получается из другой, если провести замену всех переменных на их инверсии и провести инверсию функции.

Например, f₈(х₁х₂)=х₁х₂ и f₁₄(x₁x₂)=х₁х₂ двойственны: .

Это можно доказать, построив таблицу истинности:

Таблица 26

Таблица истинности

х1	х2		х1х2
0	0	0	0
0	1	0	0
1	0	0	0
1	1	1	1

Переключательная функция называется самодвойственной, если она двойственна по отношению к самой себе: f(х₁х₂...х_n)=.

Такова, например, функция f₁₀(x₁x₂)=x₁: .

Самодвойственность устанавливается по таблице истинности следующим образом: значения функции, симметричные относительно середины таблицы инверсны. Например, для f₁₀(x₁x₂) значения функции представляют собой вектор , каждый разряд которого является инверсным по отношению к симметричному разряду относительно середины, отмеченной пунктиром. Эти разряды соответствуют инверсным наборам х₁х₂: 00-11, 01-10. Самодвойственны функции ,,х₂,х₁;

4) класс линейных функций. Переключательная (логическая) функция называется линейной, если возможно представление в виде линейного полинома, использующего функцию сложения по модулю 2:

f(x₁x₂)=с₀с₁х₁с₂х₂, где с₀,с₁,с₂ – константы 0, 1.

Например, для функции f₆(x₁x₂)=х₁х₂ при с₀=0, с₁=с₂=1:

f₆(x₁x₂)=01х₁1х₂.

Получим все линейные функции двух переменных, задав все возможные значения с₀с₁с₂ (табл. 27).

Таблица 27

Линейные функции двух переменных

с0	с1	с2	Вид полинома
0	0	0	0	Можно доказать,
0	0	1	х2	используя, например,
0	1	0	х1	таблицу истинности, что:
0	1	1	х1х2
1	0	0	1
1	0	1	1х2	=
1	1	0	1х1	=
1	1	1	1х1х2	=

Из табл. 27 видно, что каждая линейная функция имеет инверсную ей функцию: константа 0 – константа 1; повторение х₁,х₂ – инверсия ,; сложение по модулю 2 х₁х₂ – эквиваленция x₁x₂;

5) класс монотонных функций. Монотонная функция на большем сравнимом наборе переменных принимает не меньшие значения. Это удобно проверять на решетках Хассэ. Так, для двух переменных решетка имеет вид рис. 37.

Рис. 37. Решетка Хассэ для двух переменных

с указанием значений f₁₀(х₁х₂)=х₁

На рис. 37 проставлены значения монотонной функции х₁. Видно, что 11>01>00, 11>10>00 (частично упорядоченное множество наборов).

Очевидно, что константы 0, 1 – монотонные функции, дизъюнкция и конъюнкция – монотонные функции, повторения х₁, х₂ – монотонные функции.

Система логических функций называется функционально полной, если любая произвольная переключательная (логическая) функция от любого числа переменных может быть представлена в виде суперпозиции логических функций из этой системы.

Функционально полная система логических функций называется минимальной, если удаление из нее хотя бы одной функции превращает ее в неполную. Критерий функциональной полноты логических функций устанавливает теорема Поста-Яблонского, в которой утверждается, что для функциональной полноты систем логических функций необходимо и достаточно, чтобы они содержали следующие функции:

• не сохраняющую константу 0;

• не сохраняющую константу 1;

• несамодвойственную;

• нелинейную;

• немонотонную.