
- •Методические указания
- •Методические указания
- •Часть 1. Элементы линейной алгебры
- •§ 1. Определители и их скойства
- •§ 2. Матрицы и действия над ними
- •Сложение матриц. Действия над ними
- •§ 3. Системы линейных уравнений
- •Часть 2. Векторная алгебра
- •§ 1. Векторы и линейные операции над ними
- •§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
- •§ 3. Скалярное произведение векторов
- •§ 4. Векторное произведение векторов
- •§ 5. Смешаноё произведение трёх векторов
- •Часть 3. Аналитическая геаметрия на плоскости и в пространстве
- •§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
- •§ 2. Прямая линия на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •§ 3. Кривые второго порядка
- •§ 4. Плоскость
- •§ 5. Прямая в пространстве
- •Список использованной литературы
- •Методические указания
- •Методические указания
§ 3. Кривые второго порядка
Литература: (1, с.135-149; 2, с. 120-138; 3, с. 52-64; 4, с. 52-64)
Определение кривой второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае это уравнение имеет вид:
![]() (18)
(18)
где коэффициент – действительные числа и хотя бы одно из чисел А, В или С отлично от нуля.
К кривым второго порядка относятся линии: окружность, эллипс, гипербола, парабола.
Окружность
Окружностью называется совокупность точек, равноудалённых от одной и той же точки, называется центром. Уравнение окружности имеет вид:
![]() (19)
(19)
где
![]() - координаты центра окружности, а
- координаты центра окружности, а![]() - радиус окружности.
- радиус окружности.
Пример 1. Составить
уравнение окружности, которая проходит
через точку
![]() и её центр находится в точке
и её центр находится в точке![]() .
.
Решение. Воспользуемся
формулой (19). Имеем
![]() ;
;![]() .
Найдём радиус окружности
.
Найдём радиус окружности![]()
![]() .
Тогда уравнение окружности имеет вид:
.
Тогда уравнение окружности имеет вид:
![]()
Эллипс
Эллипсом называется совокупность точек, сумма расстояний которых до двух данных точек, называется фокусами, есть величина постоянная. Каноническое (простейшее) уравнение эллипса имеет вид:
![]() (20)
(20)
где
![]() - большая.
- большая.![]() - малая полуоси эллипса (рис. 6)
- малая полуоси эллипса (рис. 6)


![]() - фокусное расстояние.
- фокусное расстояние.
Связь между
![]() ,
,![]() и
и![]() определяется формулой:
определяется формулой:
![]() (21)
(21)
Форма эллипса
(мера его сжатия) характеризуется
эксцентриситетом
![]() :
:
![]() (22)
(22)
Для эллипса
![]() ,
так как
,
так как![]() .
Фокусы эллипса лежат на большой оси.
.
Фокусы эллипса лежат на большой оси.
Пример 2. Составить
каноническое уравнение эллипса,
проходящего через точки
![]() и
и![]() .
.
Решение. Каноническое
уравнение эллипса имеет вид (20):
![]() .
Так как точки
.
Так как точки![]() и
и![]() лежат на эллипсе, то их координаты
удовлетворяют уравнению (20).
лежат на эллипсе, то их координаты
удовлетворяют уравнению (20).
Имеем:

Решая систему
получим:
![]() ,
,![]() .
Следовательно, уравнение эллипса имеет
вид:
.
Следовательно, уравнение эллипса имеет
вид:![]() .
.
Гипербола
Гиперболой называется совокупность точек, разность расстояний которых до двух данных точек, называется фокусами, есть величина постоянная.
Каноническое уравнение гиперболы имеет вид:
![]() (23)
(23)
где
![]() - вещественная,
- вещественная,![]() - мнимая полуоси (рис. 7).
- мнимая полуоси (рис. 7).

![]() - фокусное расстояние.
Связь между
- фокусное расстояние.
Связь между
![]() ,
,![]() и
и![]() определяется соотношением:
определяется соотношением:
![]() (24)
(24)
Г ипербола
имеет две асимптоты, уравнения которых:
ипербола
имеет две асимптоты, уравнения которых:
![]() (25)
(25)
Отношение
![]() называется эксцентриситетом гиперболы.
Фокусы гиперболы расположены на
действительной оси.
называется эксцентриситетом гиперболы.
Фокусы гиперболы расположены на
действительной оси.
Пример 3. Составить
каноническое уравнение гиперболы,
проходящей через точку
![]() ,
зная, что её эксцентриситет равен
,
зная, что её эксцентриситет равен![]() .
.
Решение. Такая
точка М лежит на гиперболе, то её
координаты удовлетворяют уравнению
гиперболы. Подставив
![]() ,
,![]() в уравнение (23), получим
в уравнение (23), получим![]() .
Так как эксцентриситет
.
Так как эксцентриситет![]() ,
то по условию получим
,
то по условию получим![]() ,
или
,
или![]() .
Используя формулу (24), имеем
.
Используя формулу (24), имеем![]() .
Следовательно,
.
Следовательно,![]() .
Таким образом, уравнение искомой
гиперболы имеет вид
.
Таким образом, уравнение искомой
гиперболы имеет вид![]() .
.
Парабола
Параболой называется совокупность точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Каноническое уравнение параболы:
![]() (26)
(26)
где
![]() - параметр,
- параметр,![]() ,
определяет расстояние от фокуса
,
определяет расстояние от фокуса![]() до директрисы
до директрисы![]() (рис. 8)
(рис. 8)


Другие виды уравнений параболы (рис. 9)


Пример 4. Парабола
симметрична оси Ох, проходит через точку
![]() ,
а вершина его лежит в начале координат.
Составить её уравнение.
,
а вершина его лежит в начале координат.
Составить её уравнение.
Решение. Так как
парабола проходит через точку
![]() с положительной абсциссой, а её осью
служит ось Ох, то уравнение параболы
имеет вид
с положительной абсциссой, а её осью
служит ось Ох, то уравнение параболы
имеет вид![]() .
Подставив координаты тачки А в это
уравнение, получим
.
Подставив координаты тачки А в это
уравнение, получим![]() ,
,![]() .
Следовательно, искомое уравнение имеет
вид
.
Следовательно, искомое уравнение имеет
вид![]() .
.
Приведение общего уравнения кривой второго порядка к каноническому
Общее уравнение линии второго порядка имеет вид (18).
Задача упрощения такого уравнения состоит в том, чтобы в преобразованном уравнении, были устранены: 10 член, содержащий произведение текущих координат, и 2) члены, содержащие первые степени двух координат или, по крайней мере, одной из них.
Рассмотрим случай
упрощения уравнения кривой второго
порядка, когда оно не содержит произведения
текущих координат, т.е. имеет вид:
![]() .
Путём дополнения до полного квадрата
и параллельного переноса такое уравнение
сводится к одному из канонических
уравнений.
.
Путём дополнения до полного квадрата
и параллельного переноса такое уравнение
сводится к одному из канонических
уравнений.
Пример 5. Какую
линию определяет уравнение
![]() ?
?
Решение. Преобразуем данное уравнение следующим образом:
![]() ,
,
![]()
Обозначим:
![]() ,
,![]() .
.
Тогда уравнение
в новой системе
![]() с центром в точке
с центром в точке![]() примет вид:
примет вид:![]() ,
или
,
или![]() .
.
Т аким
образом, заданная кривая является
эллипсом (рис. 10).
аким
образом, заданная кривая является
эллипсом (рис. 10).

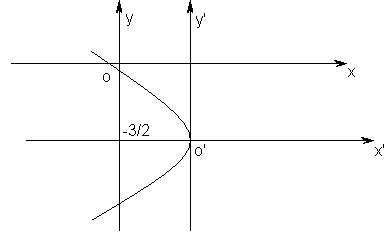
Пример 6. Какую
линию определяет уравнение
![]()
Решение. Преобразуем данное уравнение следующим образом:
![]() ;
;
![]() ;
;
![]() .
.
Обозначим:
![]() ,
,![]() .
.
Тогда уравнение
в системе
![]() с центром в точке
с центром в точке![]() примет вид
примет вид![]() .
.
Таким образом:
данная кривая – парабола с вершиной в
точке
![]() (рис. 11).
(рис. 11).

Замечание. Если уравнение линии второго порядка содержит произведение текущих координат, то путём поворота осей и надлежащим выбором угла поворота следует добиться того, чтобы преобразованном уравнении отсутствовало произведение текущих координат.
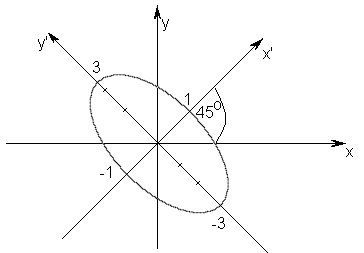
Пример 7. Привести к простейшему виду уравнение кривой
![]() .
.
Решение. Применим формулы поворота (6).
![]()
![]() ;
;
![]() .
.
Выберем угол
![]() так, чтобы
так, чтобы![]() .
.
Тогда
![]() .
.
Следовательно,
уравнение кривой в системе
![]() примет вид:
примет вид:![]() или
или![]() - эллипс (рис. 12).
- эллипс (рис. 12).

Вопросы для самопроверки
Как определяется кривая второго порядка?
Что называется окружностью и как записывается её каноническое уравнение?
Как определяется эллипс и каково его каноническое уравнение?
Определите гиперболу и запишите её каноническое уравнение.
Какая линия называется параболой и какой вид имеет её каноническое уравнение?
Как приводится уравнение кривой второго порядка к каноническому виду?
Примеры для самостоятельного решения
Написать уравнение окружности с центром в точке
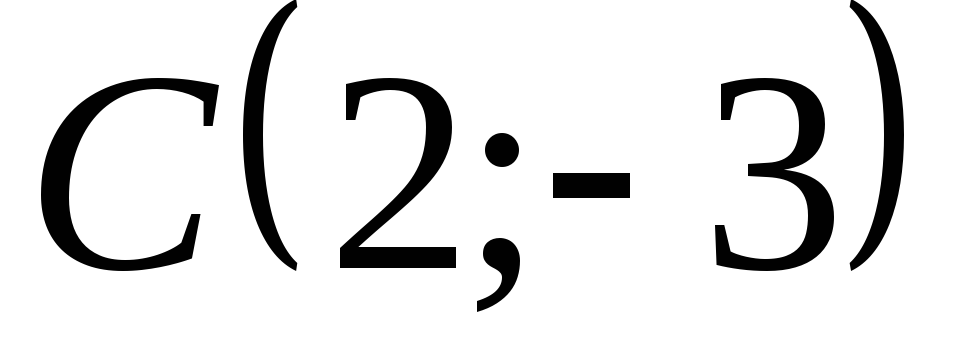 и радиусом, равным 6.
и радиусом, равным 6.Ставить уравнение окружности, проходящей через точки
 и
и ,
если её центр лежит на прямой
,
если её центр лежит на прямой .
.Найти длинны осей, координаты фокусов и эксцентриситет эллипса
 .
.Составить уравнение гиперболы, проходящей через точку
 ,
если асимптоты гиперболы имеют
уравнения
,
если асимптоты гиперболы имеют
уравнения .
.Составить простейшее уравнение параболы, если известно, что её фокус находится в точке пересечения прямой
 с осью Ох.
с осью Ох.Определить, какие кривые определяются следующими уравнениями. Построить рисунки.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() :
:
г)
![]() ;
;
д)
![]() .
.
Ответы к примерам
3.8.1.
![]() 3.8.2.
3.8.2.![]()
3.8.3.
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]()
3.8.4.
![]() 3.8.5.
3.8.5.![]()
3.8.6. а) окружность,
центр в точке
![]() ,
,![]()
б) эллипс
![]() ,
,![]()
в) гипербола
![]() ,
,![]()
г) парабола
![]() ,
,![]()
д) эллипс
![]() ;
;![]() ;
;![]() в системе
в системе![]() .
.
