§ 2. Матрицы и действия над ними

Литература: (1, с. 16-18; 2, с. 71-82; 3, с. 259-263)

1. Определение матрицы и основные понятия

Рассмотрим прямоугольную таблицу из m строк и n столбцов:

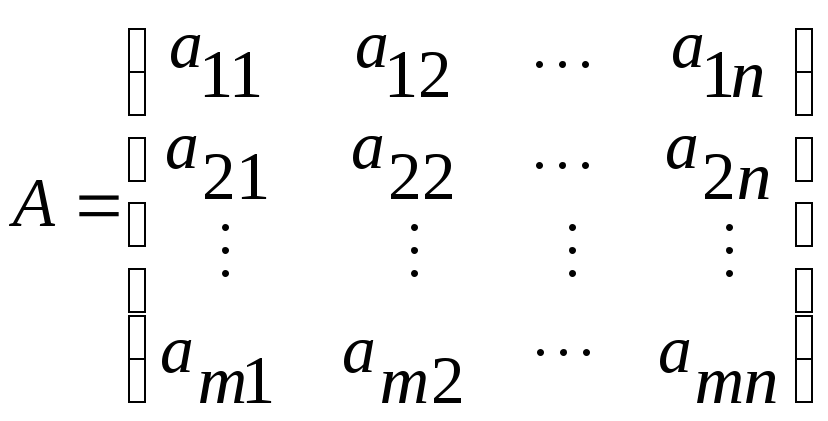
Такая таблица называется матрицей. Числа ,,,- элементы этой матрицы. Если(число строк матрицы равно числу ее столбцов), то матрица называется квадратной-го порядка. Каждая матрица имеет определённые размеры, т.е. количество строк и количество столбцов. Матрица, у которой всего один столбец, называется столбцевой или числовым вектором. Матрица у которой всего одна строка, называется строчной. Матрица, у которой все элементы равны нулю, называется нулевой. Квадратная матрица, у которой равны нулю все элементы, кроме стоящих на главной диагонали, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны единице называется единичной. Обозначим её

.

Если поменять местами строки и столбцы матрицы , то получим так называемую транспонированную матрицу

.

Квадратная матрица имеет определитель, который обозначим.

Две матрицы называются равными, если они одинакового размера и их соответствующие элементы равны . В этом случае -.

2. Сложение матриц. Действия над ними

Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов данных двух матриц . Символически это записывают.

Пример 1.

Аналогично определяется разность двух матриц.

Сложение матриц обладает переместительным и сочетательным свойствами, т.е. 1.) ;

2.) .

Умножение матрицы на число

Чтобы умножить матрицу на число , нужно каждый элемент этой матрицы умножить на это число:.

Пример 2.

.

При умножении матрицы на число справедливы следующие свойства: 1.) ; 2.); 3.).

Умножение матриц

Произведением матрицы изстрок истолбцов на матрицуизстрок истолбцов, элементкоторый равен сумме произведений элементов-й строки матрицына соответствующие элементы-го столбца матрицы, т.е.

.

Пример 3.

.

В результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица-множимое, и столько столбцов, сколько их имеет матрица множитель, т.е.. Так, произведение двух матриц 3-го порядка можно символически представить:

.

При умножении матрицы справедливы свойства:

1.) - переместительный закон не верен;

2.) ;

3.) ;

4.) ;

5.) ;

6.) .

3. Обратная матрица

Определение: Матрица называется обратной для матрицы, если.

Теорема: Для того, чтобы квадратная матрица имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Нахождение матрицы, обратной данной:

Пусть дана невырожденная матрица

, .

Можно доказать, что обратная матрица определяется равенством: ,(6)

где есть алгебраическим дополнением элементаопределителя матрицы.

Замечание: Элементами обратной матрицы являются алгебраические дополнения элементов транспонированной матрицы, деление на определитель матрицы.

Пример 4. Найти матрицу обратную данной: .

Решение: Воспользуемся формулой (6). Найдем определитель матрицы .

.

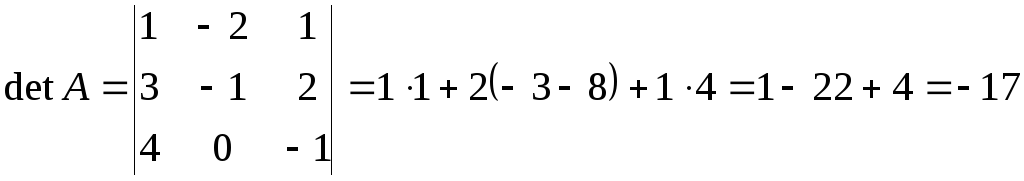Находим алгебраические дополнения:

; ;;

; ;;

; ;.

Следовательно:

.

4. Ранг матрицы

Пусть дана матрица изстрок истолбцов. Выделим в ней произвольнострок истолбцов (,). Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу-го порядка. Определитель этой матрицы называется минором-го порядка матрицы.

Наивысший из порядков миноров, отличных от нуля, называется рангом матрицы . Так, если ранг матрицы, то это означает, что среди миноров порядкаесть хотя бы один минор, не равный нулю, а все миноры высшего порядка (чем) равны нулю.

При определении ранга матрицы приходится вычислять большое количество определителей. Чтобы облегчить этот процесс, используют специальные приёмы. Вначале введем понятие элементарных преобразований матрицы:

1. умножение всех элементов какой-либо строки 9столбца) на число ;

2. прибавление к элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число;

3. перемена местами строк (столбцов) матрицы;

4. отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю;

Матрицы, полученные одна из другой при элементарных преобразованиях, называются эквивалентными. Эквивалентные матрицы имеют одинаковый ранг. .

Пример 5. Вычислить ранг матрицы

.

Решение: Используя элементарные преобразования получим:

. .

Так как минор второго порядка отличен от нуля, то .

5. Вопросы для самопроверки

Что называется матрицей? Как обозначается матрица и как определяется её размер?

Назовите виды матриц.

Как определяются линейные операции над матрицами и каковы их свойства?

Что называется произведением двух матриц? Каковы свойства произведений матриц?

Какая матрица называется обратной для данной матрицы? Всегда ли существует обратная матрица? Как можно найти обратную матрицу?

Что называется рангом матрицы и как его можно найти?

6. Примеры для самостоятельного решения

Выполнит действия:

1. ; 2.;

3. ; 4.;

5. ; 6.

7. 8.;

9. ; 10..

11. Найти , где;

12. Найти , где;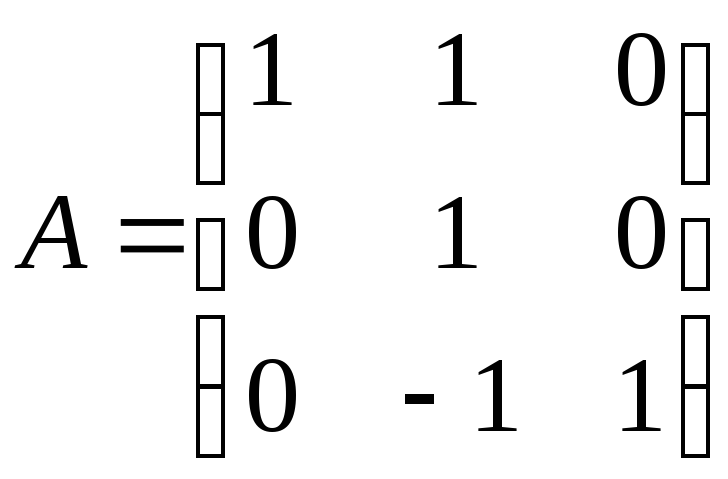

13. Найти , где,-единичная матрица

14. Найти , при;

15. Найти , при;

Найти обратную матрицу , если

16. ; 17.;

18. ; 19.;

Определить ранг матрицы :

20. ; 21.;

22. ; 23..

7. Ответы к примерам

1. ; 2. ; 3.;

4. ; 5.; 6.;

7. ; 8.; 9.;

10. ; 11.; 12.;

13. ; 14.; 15.;

16. ; 17.; 18. ;

19. ; 20.;

21. ; 22.; 23..