
- •Методические указания
- •Методические указания
- •Часть 1. Элементы линейной алгебры
- •§ 1. Определители и их скойства
- •§ 2. Матрицы и действия над ними
- •Сложение матриц. Действия над ними
- •§ 3. Системы линейных уравнений
- •Часть 2. Векторная алгебра
- •§ 1. Векторы и линейные операции над ними
- •§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
- •§ 3. Скалярное произведение векторов
- •§ 4. Векторное произведение векторов
- •§ 5. Смешаноё произведение трёх векторов
- •Часть 3. Аналитическая геаметрия на плоскости и в пространстве
- •§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
- •§ 2. Прямая линия на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •§ 3. Кривые второго порядка
- •§ 4. Плоскость
- •§ 5. Прямая в пространстве
- •Список использованной литературы
- •Методические указания
- •Методические указания
§ 3. Системы линейных уравнений
Литература: (1, с. 18-34; 2, с. 82-100; 3, с. 286-275)
Основные понятия
Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.
В системе может быть любое число уравнений с любым числом неизвестных.
Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.
Система, имеющая решение, называется совместной, в противном случае – несовместной.
Для решения системы применяют различные методы.
Решение систем
 линейных уравнений с
линейных уравнений с неизвестными
неизвестными
Пусть
![]() (число уравнений равно числу неизвестных).
(число уравнений равно числу неизвестных).
Метод Крамера
Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:
 (7)
(7)
Для нахождения
неизвестных
![]() применим формулу Крамера:
применим формулу Крамера:
![]() (8)
(8)
где
![]() - определитель системы, элементы которого
есть коэффициенты при неизвестных:
- определитель системы, элементы которого
есть коэффициенты при неизвестных:
 .
.
![]() получается путём
замены первого столбца определителя
получается путём
замены первого столбца определителя
![]() столбцом свободных членов:
столбцом свободных членов:
 .
.
Аналогично:
 ;
; .
.
Пример 1. Решить систему по формуле Крамера:
 .
.
Решение: Воспользуемся формулами (8):
 ;
;
 ;
;
 ;
;
 ;
;
Тогда
![]()
Ответ:
![]() .
.
Для любой системы
![]() линейных уравнений с
линейных уравнений с![]() неизвестными можно утверждать:
неизвестными можно утверждать:
Если определить системы
 ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.Если
 ,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если
,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если или не иметь их, если хотя бы один из
определителей
или не иметь их, если хотя бы один из
определителей не равен нулю.
не равен нулю.
Матричный способ решения
Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.
Используя правила
умножения матриц, данную систему
уравнений можно записать в виде:
![]() ,
где
,
где
 .
.
Пусть матрица
![]() невырожденная, т.е.
невырожденная, т.е.![]() .
Умножая обе части матричного уравнения
слева на матрицу
.
Умножая обе части матричного уравнения
слева на матрицу![]() ,
обратную матрице
,
обратную матрице![]() ,
получим:
,
получим:![]() .
.
Учитывая, что
![]() ,
имеем
,
имеем
![]() (9)
(9)
Пример 2. Решить систему матричным способом:
 .
.
Решение: Введём матрицы:
 -
из коэффициентов при неизвестных;
-
из коэффициентов при неизвестных;
 -
столбец свободных членов.
-
столбец свободных членов.
Тогда систему
можно записать матричным уравнением:
![]() .
.
Воспользуемся
формулой (9). Найдём обратную матрицу
![]() по формуле (6):
по формуле (6):
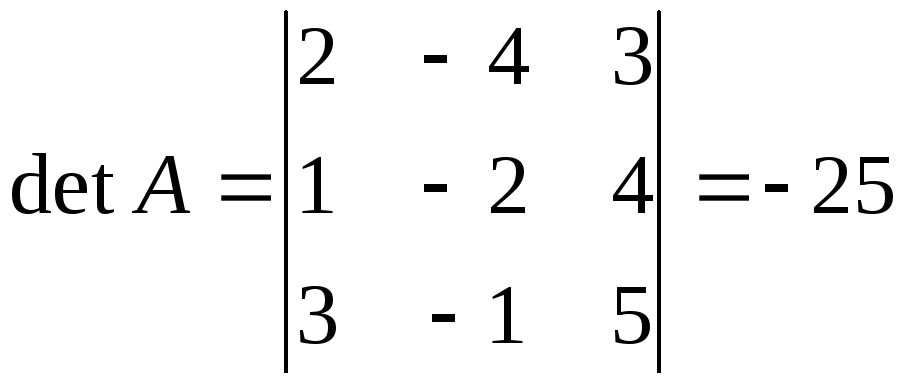 ;
;
![]()
![]()
![]()
Тогда
 .
.
Следовательно,
 Получили:
Получили:
 .
.
Ответ:
![]() .
.
Метод последовательного исключения неизвестных (метод Гаусса)
Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:
 .
. ![]()
Допустим, что
![]() (если
(если![]() ,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при
,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при![]() не равен нулю).
не равен нулю).
Первый шаг: а) делим
уравнение
![]() на
на![]() ;
б) умножаем полученное уравнение на
;
б) умножаем полученное уравнение на![]() и вычитаем из
и вычитаем из![]() ;
в) затем полученное умножаем на
;
в) затем полученное умножаем на![]() и вычитаем из
и вычитаем из![]() .
В результате первого шага будем иметь
систему:
.
В результате первого шага будем иметь
систему:

![]()
причём
![]()
![]() ,
,
![]()
![]()
Второй шаг: поступаем
с уравнением
![]() и
и![]() точно так же, как с уравнениями
точно так же, как с уравнениями![]() .
.
В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.
Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.
Пример 3. Решить методом Гаусса систему:
 .
.
Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.
 ~
~ ~
~ ~
~ ~
~
~ .
.
По полученной матрице выписываем преобразованную систему:
 .
.
Тогда
![]()
![]()
Ответ:
![]() .
.
Замечание: Если
система имеет единственное решение, то
ступенчатая система приводится к
треугольной, то есть к такой, в которой
последнее уравнение будет содержать
одно неизвестное. В случае неопределённой
системы, то есть такой, в которой число
неизвестных больше числа линейно
независимых уравнений, треугольной
системы не будет, так как последнее
уравнение будет содержать более одного
неизвестного (система имеет бесчисленное
множество решений). Когда же система
несовместна, то, после приведения её к
ступенчатому виду, она будет содержать
хотя бы одно
![]() значение вида
значение вида![]() ,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых
,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых![]() и
и![]() ).
).
Теорема существования решения системы линейных уравнений
При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.
Пусть дана система
![]() линейных уравнений с
линейных уравнений с![]() неизвестными:
неизвестными:
 (10)
(10)
Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы
 .
.
был равен рангу её расширенной матрицы
 .
.
Причём, если
![]() ,
то система (10) имеет единственное решение;
если же
,
то система (10) имеет единственное решение;
если же![]() ,
то система имеет бесчисленное множество
решений.
,
то система имеет бесчисленное множество
решений.
Линейная, однородная система
 уравнений с
уравнений с неизвестными
неизвестными
Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:
 .
.
Эта система всегда
совместна, так как она имеет нулевое
решение
![]() .
.
В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.
Терема. Для того,
чтобы однородная система линейчатых
уравнений имела нулевое решение,
необходимо и достаточно, чтобы её
определитель
![]() был равен нулю:
был равен нулю:
 .
.
Таким образом,
если
![]() ,
то решение
,
то решение![]() - единственное. Если
- единственное. Если![]() ,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае
,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае![]() .
.
Можно доказать,
что если
![]() ,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
Пример 4. Найти все решения системы:
 .
.
Решение. Определитель этой системы
 .
.
Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:
![]() .
.
Полагая, например,
![]() ,
получим
,
получим
![]() .
.
Решая систему двух
линейных уравнений, выразим
![]() и
и![]() через
через![]() :
:![]() .
Следовательно, решение системы можно
записать в виде:
.
Следовательно, решение системы можно
записать в виде:![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
Пример 5. Найти все решения системы:
 .
.
Решение. Нетрудно
видеть, что в данной системе только одно
независимое уравнение (два других ему
пропорциональны). Система из трёх
уравнений с тремя неизвестными свелась
к одному уравнению с тремя неизвестными.
Появляются два свободных неизвестных.
Найдя, например, из первого уравнения
![]() при произвольных
при произвольных![]() и
и![]() ,
получим решения данной системы. Общих
вид решения можно записать
,
получим решения данной системы. Общих
вид решения можно записать![]() ,
где
,
где![]() и
и![]() - произвольные числа.
- произвольные числа.
Вопросы для самопроверки
Сформулируйте
правило Крамера для решения системы
![]() линейных уравнений с
линейных уравнений с![]() неизвестными.
неизвестными.
В чём сущность матричного способа решения систем?
В чём заключается метод Гаусса решения системы линейных уравнений?
Сформулируйте теорему Кронекера-Капелли.
Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.
Примеры для самостоятельного решения
Найдите все решения систем:
1.
![]() ; 2.
; 2.![]() ;
;
3.
![]() ; 4.
; 4.![]() ;
;
5.
![]() ; 6.
; 6.![]() ;
;
7.
 ; 8.
; 8. ;
;
9.
 ; 10.
; 10. ;
;
11.
 ; 12.
; 12. ;
;
13.
 ;
14.
;
14.
 ;
;
15.
 .
.
Определите, при
каких значениях
![]() и
и![]() система уравнений
система уравнений
а) имеет единственное решение;
б) не имеет решения;
в) имеет бесконечно много решений.
16.
![]() ; 17.
; 17. ;
;
Найти все решения следующих однородных систем:
18.
 ; 19.
; 19.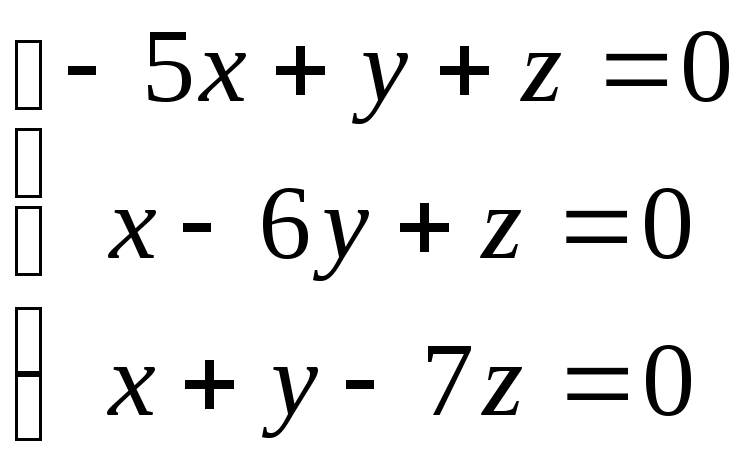 ;
;
20.
 ; 21.
; 21. ;
;
22.
 ; 23.
; 23. ;
;
Ответы к примерам
1.
![]() ; 2.
; 2.![]() ; 3.
Ǿ; 4. Ǿ;
; 3.
Ǿ; 4. Ǿ;
5.
![]() - произвольное число.
- произвольное число.
6.
![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
7.
![]() ; 8.
; 8.![]() ; 9.
Ǿ; 10. Ǿ;
; 9.
Ǿ; 10. Ǿ;
11.
![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
12.
![]() ,
где
,
где![]() и
и![]() - произвольные числа.
- произвольные числа.
13.
![]() ; 14.
; 14. где
где![]() и
и![]() - произвольные числа.
- произвольные числа.
15. Ǿ; 16. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
17. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
18.
![]() ; 19.
; 19.![]() ; 20.
; 20.![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
21.
![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
22.
![]() ,
где
,
где![]() - произвольное число.
- произвольное число.
23.
![]() ,
где
,
где![]() и
и![]() - произвольные числа.
- произвольные числа.
