
- •Методические указания
- •Методические указания
- •Часть 1. Элементы линейной алгебры
- •§ 1. Определители и их скойства
- •§ 2. Матрицы и действия над ними
- •Сложение матриц. Действия над ними
- •§ 3. Системы линейных уравнений
- •Часть 2. Векторная алгебра
- •§ 1. Векторы и линейные операции над ними
- •§ 2. Декартовые прямоугольные координаты в пространстве. Разложение вектора по ортам
- •§ 3. Скалярное произведение векторов
- •§ 4. Векторное произведение векторов
- •§ 5. Смешаноё произведение трёх векторов
- •Часть 3. Аналитическая геаметрия на плоскости и в пространстве
- •§ 1. Предмет аналитической геометрии. Простейшие задачи. Преобразование координат
- •§ 2. Прямая линия на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •§ 3. Кривые второго порядка
- •§ 4. Плоскость
- •§ 5. Прямая в пространстве
- •Список использованной литературы
- •Методические указания
- •Методические указания
§ 5. Прямая в пространстве
Литература: (2, с. 144-151; 3, с. 248-252; 4, с. 48-52)
Общие уравнения прямой
Прямая в пространстве определяется как линия пересечения непараллельных плоскостей. При этом уравнения плоскостей описывают прямую и называются её общими уравнениями:
 (35)
(35)
Уравнения (35)
определяет прямую, если коэффициенты
![]() не пропорциональны коэффициентам
не пропорциональны коэффициентам![]() .
.
Канонические уравнения прямой
Пусть прямая
![]() проходит через точку
проходит через точку![]() параллельно вектору
параллельно вектору![]() .
Всякий вектор
.
Всякий вектор![]() ,
параллельный прямой, называется
направляющим вектором прямой.
,
параллельный прямой, называется
направляющим вектором прямой.
Канонические уравнения прямой имеют вид:
![]() (36)
(36)
Чтобы перейти от общих уравнений прямой к каноническим, необходимо:
найти какую-либо точку
 .
Для этого следует задать числовое
значение одной из неизвестных координат
точки
.
Для этого следует задать числовое
значение одной из неизвестных координат
точки и подставить его вместо соответствующей
переменной в уравнения (35), после этого
две другие координаты определяются в
результате совместного решения уравнения
(35);
и подставить его вместо соответствующей
переменной в уравнения (35), после этого
две другие координаты определяются в
результате совместного решения уравнения
(35);найти направляющий вектор
 .
В качестве вектора
.
В качестве вектора можно взять любой вектор, перпендикулярный
векторам
можно взять любой вектор, перпендикулярный
векторам и
и ,
например их векторное произведение
,
например их векторное произведение .
.
Пример 1. Найти
канонические уравнения прямой
![]() и
и![]() .
.
Решение. Выберем
произвольную точку на прямой, пологая,
например,
![]() .
.
Получим:
![]()
Решая эту систему,
найдём
![]() ,
,![]() .
За направляющий вектор прямой примем
векторное произведение векторов
.
За направляющий вектор прямой примем
векторное произведение векторов![]() и
и![]() :
:

Следовательно, искомая прямая определяется уравнением
![]()
Параметрические уравнения прямой
Уравнение вида
![]() ;
;
![]() ;
;![]() (37)
(37)
называются
параметрическими уравнениями прямой,
проходящей через точку
![]() и имеющей направляющий вектор
и имеющей направляющий вектор![]() .
В уравнениях (37)
.
В уравнениях (37)![]() рассматривается как произвольно
изменяющийся параметр.
рассматривается как произвольно
изменяющийся параметр.
Угол между прямыми. Условия параллельности и перпендикулярности прямых
Угол между двумя
прямыми определяется как угол между их
направляющими векторами
![]() и
и![]() находится по формуле:
находится по формуле:
 (38)
(38)
Условие параллельности прямых:
![]() (39)
(39)
Условие перпендикулярности прямых:
![]() (40)
(40)
В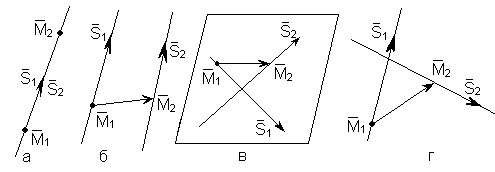
 озможны
следующие четыре случая (рис. 13) взаимного
расположения прямых
озможны
следующие четыре случая (рис. 13) взаимного
расположения прямых
а – прямые сливаются:
![]() ;
;
б![]() – прямые параллельны:
– прямые параллельны:![]()
![]()
![]() ,
но
,
но![]() ;
;
в – прямые
пересекаются:
![]()
![]() ,
но
,
но![]() ;
;
![]() ,
,![]() -
-
компланарны, т.е.
![]() ,
,
![]() .
.
Пример 2. Определить угол между прямыми:
![]() ;
;
![]()
Решение. Из
канонических уравнений прямых определим
их направляющие векторы
![]() и
и![]()
Тогда согласно формуле(38) имеем:
![]()
Следовательно.
![]() .
.
Пример 3. Доказать, что прямые
![]() и
и
![]()
пересекаются и найти их точку пересечения.
Решение. Из
канонических уравнений прямых определим
направляющие векторы
![]() ,
,![]() и точки, через которые проходят прямые
и точки, через которые проходят прямые![]() ,
,![]() .
.
Найдём смешанное произведение векторов:
![]() ,
,
![]() ,
,![]() ;
;

Следовательно,
эти векторы компланарны, и две прямые
лежат в одной плоскости. Прямые
пересекаются, так как векторы
![]() и
и![]() неколлинеарные.
неколлинеарные.
Точку пересечения
прямых найдём, например, так: приведём
уравнение одной из прямых к параметрическому
виду и из уравнения второй прямой найдём
значение параметра
![]() ,
отвечающее точке пересечении.
,
отвечающее точке пересечении.
Параметрические
уравнения первой прямой:
![]() ;
;![]() ;
;![]()
Тогда, подставляя
эти выражения для
![]() в уравнение второй прямой, получим:
в уравнение второй прямой, получим:
![]()
Следовательно,
точка пересечения
![]() ;
;
![]() ;
;
![]()
Прямая и плоскость в пространстве. Угол между прямой и плоскостью
У глом
между прямой и плоскостью называется
угол
глом
между прямой и плоскостью называется
угол![]() между прямой и её проекцией на эту
плоскость (рис. 14).
между прямой и её проекцией на эту
плоскость (рис. 14).

Этот угол определяется по формуле:
![]() (41)
(41)
Условие параллельности прямой и плоскости:
![]() ,
т.е.
,
т.е.
![]() (42)
(42)
Условие перпендикулярности:
![]() ,
т.е.
,
т.е.
![]() (43)
(43)
Пример 4. Найти
угол между прямой
![]() и плоскостью
и плоскостью![]() .
.
Решение. Найдём направляющий вектор прямой:

Из уравнения
плоскости заключаем, что нормальный
вектор плоскости
![]() .
Тогда по формуле (41) имеем:
.
Тогда по формуле (41) имеем:
![]() ;
;
![]()
Пример 5. Найти
точку пересечения прямой
![]() и плоскости
и плоскости![]()
Решение. Приведём
уравнение прямой к параметрическому
виду, приравнивая к
![]() каждоё из трёх данных отношений:
каждоё из трёх данных отношений:
![]() ,
,
![]() ,
,![]()
Подставляя
![]() в уравнение плоскости, получим значение
параметра
в уравнение плоскости, получим значение
параметра![]() ,
отвечающее точке пересечения:
,
отвечающее точке пересечения:
![]()
Искомая точка пересечения прямой и плоскости имеет координаты:
![]() ;
;
![]() ;
;![]() .
.
Пример 6. Составить уравнение плоскости, проходящей через две параллельные прямые
![]() ,
,
![]() .
.
Решение. Так как
две прямые лежат в плоскости, то в ней
лежат вектора
![]() - направляющий и
- направляющий и![]() ,
соединяющий точки
,
соединяющий точки
![]() и
и![]() .
Взяв текущую точку плоскости
.
Взяв текущую точку плоскости![]() и соединив её с одной из точек, например,
и соединив её с одной из точек, например,![]() получим вектор
получим вектор![]() ,
принадлежащий плоскости. Следовательно,
векторы
,
принадлежащий плоскости. Следовательно,
векторы![]() ,
,![]() и
и![]() компланарны, т.е.
компланарны, т.е.
![]() .
Получим:
.
Получим:
 .
.
Для наглядности полезно сделать рис. 15.



Вопросы для самопроверки
Как определяются общее уравнения прямой?
Какие уравнения прямой называются каноническими? Что называется направляющим вектором прямой?
Как перейти от общих уравнений прямой к каноническим?
Как записываются параметрические уравнения прямой?
Как определяется угол между прямыми? Сформулируйте условия параллельности и перпендикулярности между прямой и плоскостью.
Примеры для самостоятельного решения
Составить канонические уравнения прямой, проходящей через точку
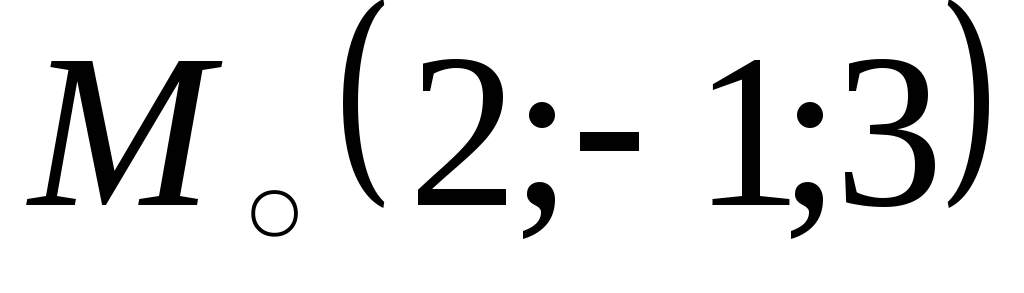 :
а) вектору
:
а) вектору ;
б) прямой
;
б) прямой ;
в) оси
;
в) оси
Составить параметрические уравнения прямой, проходящей через точки
 и
и .
.Составить канонические уравнения прямой

Найти острый угол между прямыми
 и
и .
.Составить уравнение прямой, проходящей через точку
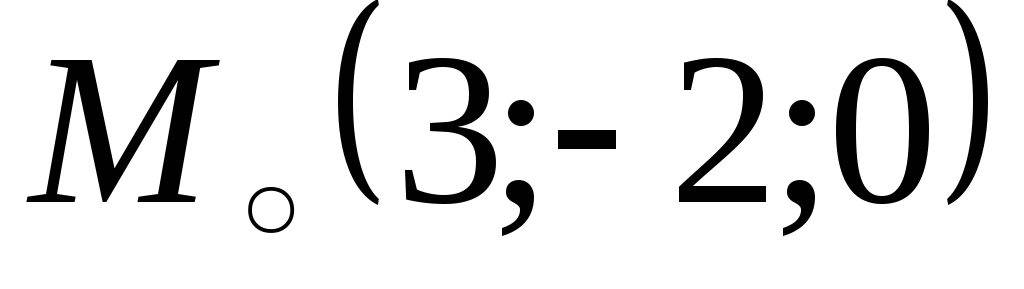 перпендикулярную к прямой
перпендикулярную к прямой и лежащей в плоскости
и лежащей в плоскости .
.Составить уравнение прямой, проходящей через точку
 параллельно линии пересечения
плоскостей
параллельно линии пересечения
плоскостей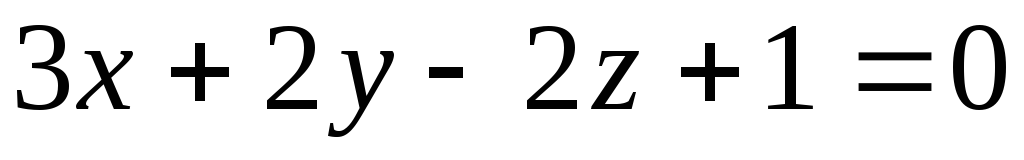 и
и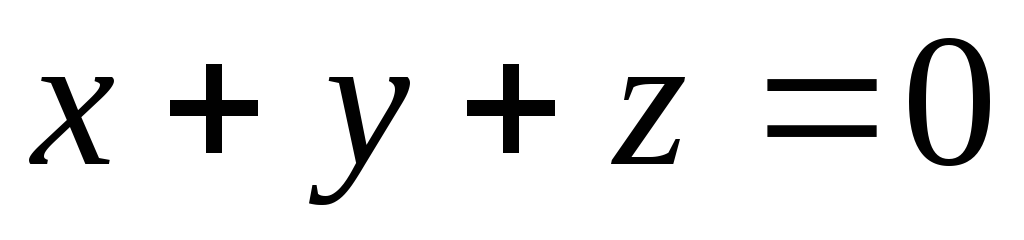 .
.Доказать, что прямые
 и
и пересекаются, и найти их точку
пересечения.
пересекаются, и найти их точку
пересечения.Вычислить угол между прямой
 и плоскостью
и плоскостью .
.Найти проекцию точки
 на плоскость
на плоскость .
.Провести плоскость через прямую
 и точку
и точку .
.Проверить, что прямые
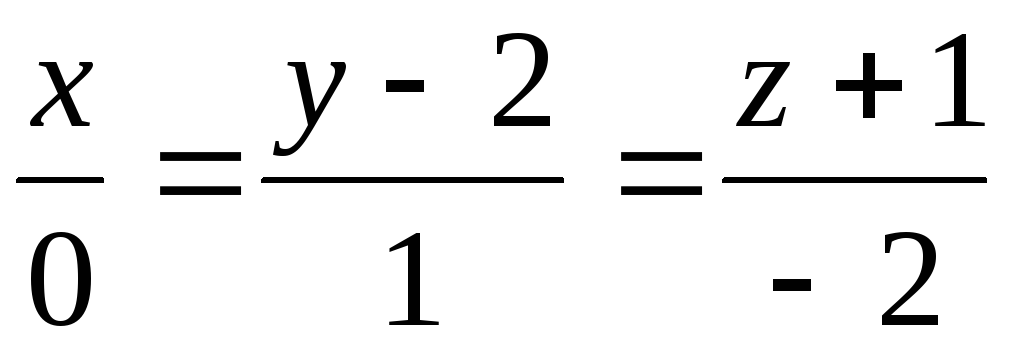 и
и пересекаются. Найти уравнения плоскости,
в которой они лежат.
пересекаются. Найти уравнения плоскости,
в которой они лежат.Вычислить расстояние
 точки
точки от прямой
от прямой .
.Составить уравнение плоскости, проходящей через прямую
 ,
, ,
, параллельно прямой
параллельно прямой .
.Найти точку, симметричную точке
 относительно плоскости, проходящей
через
относительно плоскости, проходящей
через ,
, и
и .
.
Ответы к примерам
5.7.1. а)
![]() б)
б)![]()
в)
![]() 5.7.2.
5.7.2.![]() ,
,![]() ,
,![]()
5.7.3.
![]() 5.7.4.
5.7.4.![]()
5.7.5.
![]() 5.7.6.
5.7.6.![]()
5.7.7.
![]() 5.7.8.
5.7.8.![]()
5.7.9.
![]() 5.7.10.
5.7.10.![]()
5.7.11.
![]() 5.7.12.
5.7.12.![]()
5.7.13.
![]() 5.7.14.
5.7.14.![]()
