3.3. Теореми Куна-Таккера

У попередньому розділі побудовані умови Куна-Таккера для задач умовної оптимізації. За допомогою методу множників Лагранжа отримано інтуїтивне уявлення про те, що умови Куна - танкер тісно пов'язані з необхідними умовами оптимальності. У даному розділі розглядаються строгі формулювання необхідних і достатніх умов оптимальності рішення задачі нелінійного програмування. Теорема 1. Необхідність умов Куна-Таккера Розглянемо завдання нелінійного програмування (0) - (2). Нехай - Диференційовні функції, а х * - допустиме рішення даного завдання. Покладемо . Далі нехай лінійно незалежні. Якщо х * - оптимальне рішення задачі нелінійного програмування, то існує така пара векторів , Що є рішенням задачі Куна-Таккера (3) - (7). Умова, згідно з яким повинні бути лінійно незалежними, відоме як умова лінійної незалежності і по суті являє собою деяке умова регулярності допустимої області, яке майже завжди виконується для зустрічаються на практиці завдань оптимізації. Проте взагалі перевірка виконання умови лінійної незалежності певні складнощі, тому що потрібно, щоб оптимальне рішення задачі було відомо заздалегідь. Разом з тим умова лінійної незалежності завжди виконується для задач нелінійного програмування, що володіють такими властивостями. 1. Всі обмеження у вигляді рівностей та нерівностей містять лінійні функції. 2. Всі обмеження у вигляді нерівностей містять увігнуті функції, всі обмеження-рівності - лінійні функції, а також існує, принаймні, одна допустима точка х, яка розташована у внутрішній частині області, яка визначається обмеженнями-нерівностями. Іншими словами, існує така точка х, що

Якщо умова лінійної незалежності в точці оптимуму не виконується, то завдання Куна-Таккера може не мати рішення. Приклад 4 Мінімізувати при обмеженнях Рішення. На рис.1 зображена область допустимих рішень сформульованої вище нелінійної задачі. Ясно, що оптимальне рішення цього завдання є . Покажемо, що умова лінійної незалежності не виконується в точці оптимуму.

Рис.1 Допустима область в задачі 4
Так як
Легко бачити, що вектори лінійно залежні, тобто умова лінійної незалежності в точці не виконується.
Запишемо умови Куна-Таккера і перевіримо, чи виконуються вони в точці (1, 0). Умови (3), (6) і (7) приймають такий вигляд;
(11)
(12)
(13)
(14)
(15)
(16)
Приз рівняння (11) випливає, що , Тоді як рівняння (14) дає , Отже, точка оптимуму не є точкою Куна - Таккера.
Зауважимо, що порушення умови лінійної незалежності не обов'язково означає, що точка Куна-Таккера не існує. Для того щоб підтвердити це, замінимо цільову функцію з цього прикладу функцією. При цьому оптимум, як і раніше досягається в точці (1,0), в якій умова лінійної незалежності не виконується. Умови Куна-Таккера (12) - (16) залишаються незмінними, а рівняння (11) набуває вигляду

Неважко перевірити, що точкає точкою Куна-Таккера, тобто задовольняє умовам Куна-Таккера.
Теорема про необхідність умов Куна-Таккера дозволяє ідентифікувати неоптимальні точки. Іншими словами, теорему 1 можна використовувати для доказу того, що задана допустима точка, яка задовольняє умові лінійної незалежності, не є оптимальною, якщо вона не задовольняє умовам Куна-Таккера. З іншого боку, якщо в цій точці умови Куна-Таккера виконуються, то немає гарантії, що знайдено оптимальне рішення нелінійної задачі. Як приклад розглянемо таку задачу нелінійного програмування.
Наступна теорема встановлює умови, при виконанні яких точка Куна-Таккера автоматично відповідає оптимальному вирішенню задачі нелінійного програмування.
Теорема.2 Достатність умов Куна-Таккера
Розглянемо завдання нелінійного програмування (0) - (2). Нехай цільова функціяопукла, всі обмеження у вигляді нерівностей містять увігнуті функції , А обмеження у вигляді рівностей містять лінійні функції . Тоді якщо існує рішення , Що задовольняє умовам Куна-Таккера (3) - (7), то x * - оптимальне рішення задачі нелінійного програмування.
Якщо умови теореми 2 виконуються, то знаходження точки Куна-Таккера забезпечує отримання оптимального розв'язку задачі нелінійного програмування.
Теорему 2 можна також використовувати для доказу оптимальності даного рішення задачі нелінійного програмування. В якості ілюстрації знову розглянемо приклад:
Мінімізувати
при обмеженнях
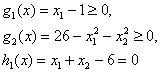
За допомогою теореми 2 доведемо, що рішенняє оптимальним. Маємо

Так як матрицяпозитивно полуопределена при всіх х, функція виявляється опуклою. Перше обмеження у вигляді нерівності містить лінійну функцію , Яка одночасно є як опуклої, так і увігнутої. Для того
щоб показати, що функціяє увігнутою, обчислимо

Оскільки матрицянегативно визначена, функція є увігнутою. Функція входить в лінійне обмеження в вяде рівності. Отже, всі умови теореми 2 виконані; якщо ми покажемо, що - Точка Куна-Таккера, то дійсно встановимо оптимальність рішення . Умови Куна-Таккера для прикладу 2 мають вигляд
(22)
(23)
(24)
(25)
, (26)
, (27)
(28)
(29)
Точказадовольняє обмеженням (24) - (26) і, отже, є допустимими. Рівняння (22) і (23) приймають такий вигляд:

Поклавши, Отримаємо і . Таким чином, рішення x *= (1, 5), задовольняє умовам Куна-Таккера. Оскільки умови теореми 2 виконані, то оптимальне вирішення завдання з прикладу 3. Зауважимо, що існують також і інші значення і , Які задовольняють систему (22) - (29).
Зауваження
1.Для зустрічаються на практиці завдань умова лінійної незалежності, як правило, виконується. Якщо в задачі всі функції диференційовні, то точку Куна-Таккера слід розглядати як можливу точку оптимуму. Таким чином, багато хто з методів нелінійного програмування сходяться до точки Куна-Таккера. (Тут доречно провести аналогію з випадком безумовної оптимізації, коли відповідні алгоритми дозволяють визначити стаціонарну крапку.)
2. Якщо умови теореми 2 виконані, точка Куна-Таккера в той же час виявляється точкою глобального мінімуму. На жаль, перевірка достатніх умов дуже складною, і, крім того, прикладні задачі часто не володіють необхідними властивостями. Слід зазначити, що наявність хоча б одного нелінійного обмеження у вигляді рівності призводить до порушення припущень теореми 2.
3.Достаточние умови, встановлені теоремою 2, можна узагальнити на випадок завдань з неопуклих функціями, що входять в обмеження у вигляді нерівностей, неопуклих цільовими функціями і нелінійними обмеженнями-рівностями. При цьому використовуються такі узагальнення опуклих функцій, як квазівипуклие і псевдовипуклие функції.