ДРТЦ дляЗАО / Лекция №14

Лекция №14

Тема: Спектральный метод анализа

переходных процессов

Учебные вопросы

1 Основы спектрального метода анализа переходных процессов.

2 Понятие о преобразовании Фурье.

3 Алгоритм анализа переходных процессов спектральным методом.

Литература: [2] с.174-196.

1 Основы спектрального метода анализа переходных процессов

Известно, что сигналы и воздействия на электрические цепи могут быть представлены двумя равнозначными математическими моделями: временной и частотной.

Метод анализа переходных процессов, основанный на частотных моделях, называется спектральным методом.

В основе спектрального метода анализа реакции линейных цепей на внешнее воздействие лежит тот факт, что установившаяся реакция цепей на воздействие гармонического характера также является гармонической. Это обстоятельство использовалось ранее при рассмотрении метода комплексных амплитуд.

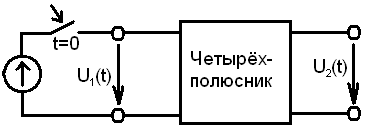
Пусть дан пассивный линейный четырехполюсник, на входные зажимы которого в момент времени t = 0 подан сигнал в виде гармонической функции (рис.14.1)

Рис. 14.1

Связь выходного U₂(t) и входного U₁(t) сигналов в общем случае описывается дифференциальным уравнением следующего вида:

(14.1)

где a_k, b_k – коэффициенты уравнения, некоторые постоянные числа, обусловленные параметрами цепи, причем

Решение уравнения (14.1) состоит из двух частей:

- решения, определяющего свободное движение;

- решения, определяющего вынужденное движение под действием сигнала U₁(t).

Уравнение свободного движения имеет вид

(14.2)

где - корни характеристического уравнения четырёхполюсника

,

имеющие отрицательные вещественные части (для пассивной цепи это условие всегда выполняется).

Определим вынужденную составляющую. Для этого запишем выражения для входного воздействия U₁(t) в следующем виде:

(14.3)

Определим вынужденную составляющую, обусловленную каждым слагаемым из правой части (14.3), после чего сложим результаты.

Для этого положим вначале, что

(14.4)

Решение уравнения (14.1) при U₁(t) = U₁₁(t) будем искать в виде

(14.5)

где U_21в(t) – составляющая вынужденного движения U_2в(t), вызванная воздействием U₁₁(t);

- некоторая неизвестная функция аргумента

После подстановки (14.4) и (14.5) в (14.1) получаем

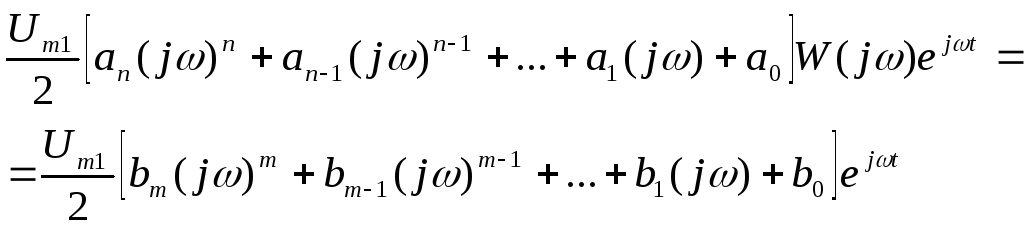(14.6)

Отсюда получаем выражение для :

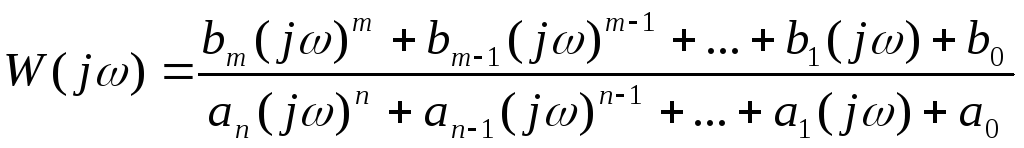(14.7)

Выражение для можно записать в показательной форме

(14.8)

Подставив (14.8) в (14.5), найдем

(14.9)

Для нахождения второй составляющей вынужденного движения положим

Выполнив аналогичные преобразования, получим

(14.10)

Следовательно,

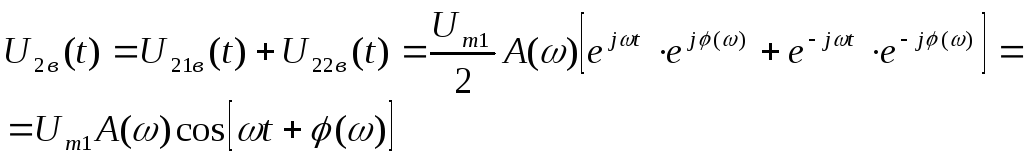(14.11)

Таким образом, доказано, что при приложении гармонического воздействия к линейному четырехполюснику после затухания свободного движения на его выходе устанавливается гармонический процесс, амплитуда которого изменяется в A(w) раз, а фаза – на угол относительно входного воздействия.

Для определения физического смысла функции найдем, при нулевых начальных условиях преобразования Фурье для левой и правой частей уравнения (14.1), полагая входное воздействие U₁(t) произвольным, имеющим преобразование Фурье:

(14.12)

где преобразование Фурье для входного сигнала

преобразование Фурье для выходного сигнала

Из (14.12) находим отношение :

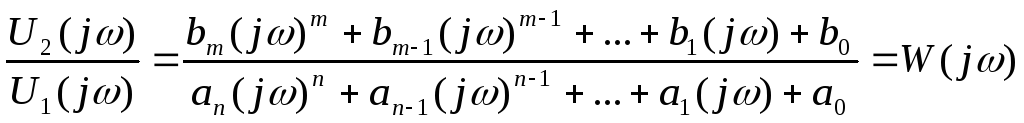(14.13)

Таким образом, функция W(jw) является отношением изображения по Фурье выходного и входного сигналов линейного четырехполюсника при нулевых условиях и представляет собой комплексную передаточную функцию (комплексный коэффициент передачи) цепи.

Выражения (14.7) и (14.13) определяют W(jw) через коэффициенты дифференциального уравнения цепи.

Если входной сигнал представляет собой сумму гармонических колебаний, то выходной сигнал можно найти как сумму гармонических колебаний с амплитудами и начальными фазами, определенными из (14.11).

2 Понятие о преобразовании Фурье

Связь между временной и частотной моделями сигнала задается с помощью прямого и обратного преобразований Фурье.

Пусть периодический сигнал S(t),тогда его спектральной моделью является комплексная функция

(14.14)

Интеграл (14.14) называется прямым преобразованием Фурье.

Кроме этого математического термина для обозначения операции (14.14) в технике широко применяются выражения:

- изображение сигнала по Фурье;

- спектральная функция (характеристика);

- спектральная плотность сигнала.

Последний термин наиболее физичен, если учесть, что размерность изображения есть [амплитуда / Гц]. Если сигнал, например, напряжение, то размерность – [В / Гц].

Таким образом, смысл изображения – плотность амплитуд на частотной оси, S(jw) является прямым преобразованием Фурье сигнала S(t).

Обратное преобразование Фурье имеет вид:

(14.15)

Таким образом, сигнал S(t) и его спектральная плотность S(jw) однозначно связаны прямым и обратным преобразованием Фурье.

Это значит, что сигнал S(t) допускает две равноправные математические модели – функцию во временной области и функцию в частотной.

С целью интерпретации полученных результатов и уяснения физического смысла понятия спектральной плотности сигнала S(t) перейдем в (14.14) к тригонометрической форме записи комплексных чисел:

(14.16)

где

а (14.17)

, (14.18) – амлитудно-частотная характеристика спектра (амплитудный спектр) периодического сигнала S(t);

, (14.19) – фазочастотная характеристика спектра (фазовый спектр) периодического сигнала S(t).

Модуль S(w) является четной функцией частоты w, а фаза – нечетной.

Теперь интегральное преобразование (14.15) нетрудно привести к тригонометрической форме:

Из четности модуля и нечетности фазы следует, что подынтегральная функция во втором интеграле является нечетной относительно w. Следовательно, второй интеграл равен нулю и окончательно имеем

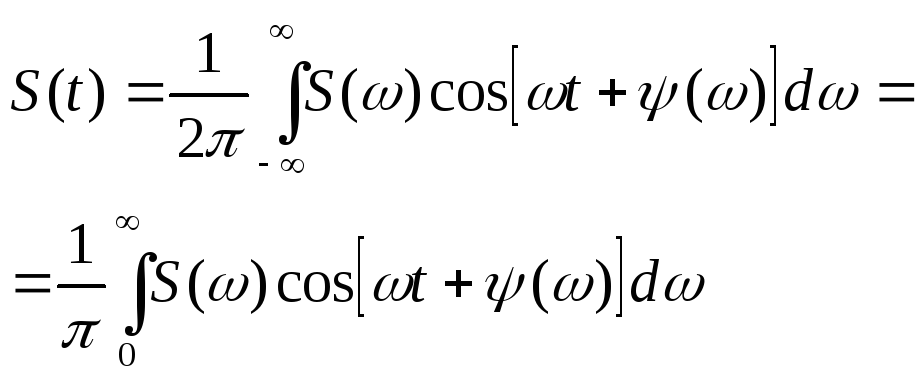(14.18)

Таким образом, на основе выражения (14.18) можно сделать следующие выводы:

1. периодический сигнал S(t) можно представить суммой бесконечного числа гармонических составляющих, каждая из которых имеет бесконечно малую амплитуду 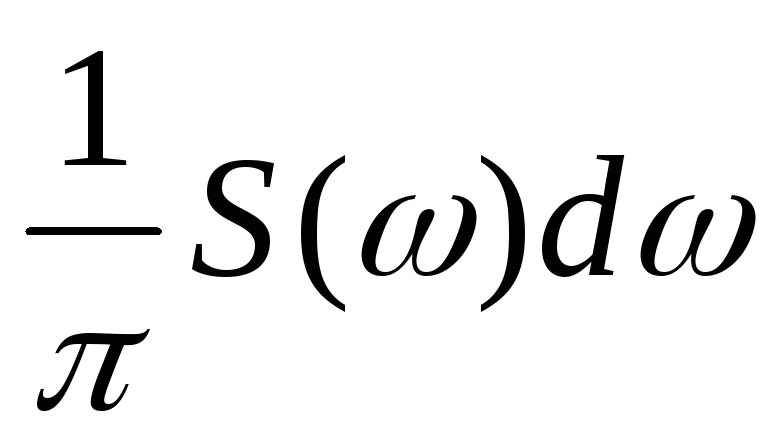, частоту w и начальную фазу;

2. модуль спектральной плотности есть коэффициент пропорциональности между амплитудой элементарного колебания и длиной бесконечно малого интервала частот, включающего в себя рассматриваемую частоту w.

Спектральный метод чрезвычайно обогащает теорию сигналов. Наиболее важным в этом смысле является то, что спектральные представления сигналов существенно улучшают анализ прохождения сигналов через широкий класс электро- и радиотехнических цепей.

В ряде случаев анализ переходных процессов спектральным методом оказывается проще, чем решение дифференциального уравнения.

Спектральный метод распространяется и на непериодические входные сигналы.

Действительно, если входное воздействие U₁(t) задано своим преобразованием Фурье

(14.19)

где

(14.20)

то воспользовавшись формулой (14.18), сигнал U₁(t) можно описать следующим соотношением:

(14.21)

Следовательно, непериодическое воздействие U₁(t) можно представить бесконечной суммой гармонических слагаемых вида

Определяя амплитуду и начальную фазу выходного гармонического колебания, соответствующего каждому такому слагаемому, и суммируя их, определим искомый выходной сигнал цепи.

Проиллюстрируем это принципиальное положение следующими выкладками.

Умножая в соответствии с (14.11) амплитуду каждого элементарного слагаемого в (14.20) на A(w) и добавляя к фазе слагаемое, получим выражение для выходного сигнала цепи U(t) в следующем виде:

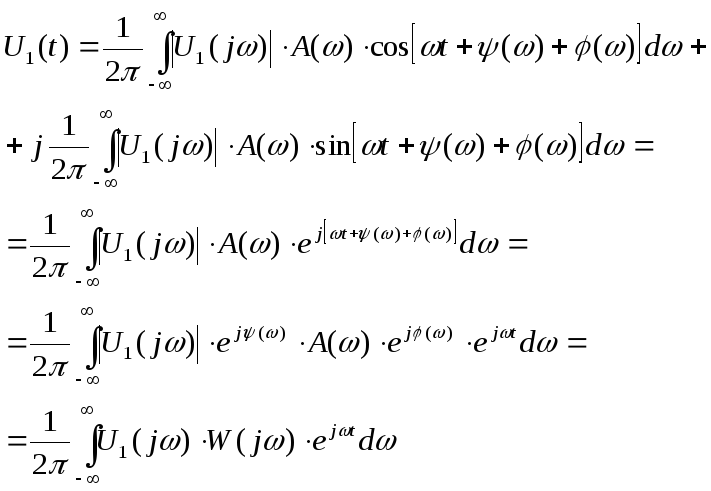
Таким образом, приходим к основной формуле спектрального метода, определяющей выходной сигнал цепи U₂(t)

(14.22)

Формула (14.22) может быть получена формально и из выражения (14.7)

(14.23)

Пользуясь далее обратным преобразованием Фурье, находим из (14.23)

Таким образом, из (14.23) следует, что анализ цепей в частотной области отличается замечательным качеством – эффект преобразования сигнала в цепи отображается алгебраической операцией умножения изображения входного сигнала на комплексную передаточную функцию цепи.

Практическая ценность спектрального метода определения выходного сигнала цепи в переходном режиме в каждом конкретном случае зависит от того, удается ли выполнить интегрирование в формуле (14.22).

3 Алгоритм анализа переходных процессов спектральным методом.

Алгоритм анализа переходных процессов спектральным методом включает следующие этапы:

1. определение спектральной плотности входного сигнала согласно (14.20);

2. определение комплексной передаточной функции цепи согласно (14.7) или (14.8);

3. определение спектральной плотности выходного сигнала согласно (14.23);

4. определение выходного сигнала по его спектральной плотности согласно (14.22).

Проиллюстрируем этот алгоритм на следующем примере.

Пример. С помощью спектрального метода определить реакцию RC – цепи (рис.14.2,а) на экспоненциальный видеоимпульс напряжения

t > 0 (рис.14.2,б).

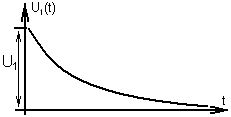
а) б)

Рис. 14.2

Решение

1. Определяем спектральную плотность входного сигнала

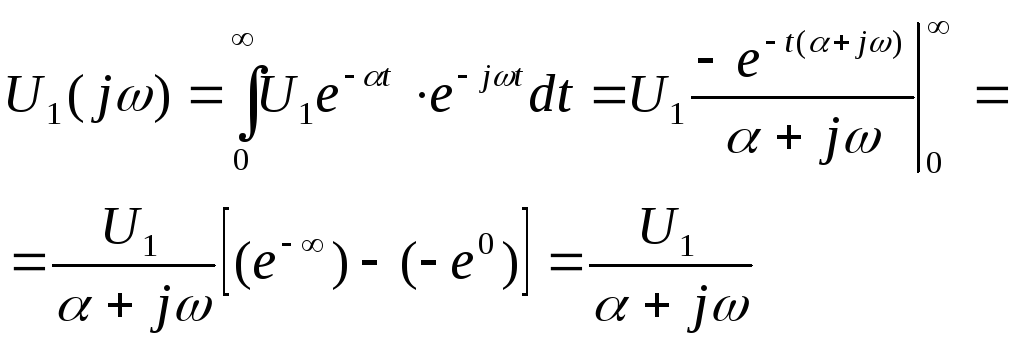(14.24)

2. Частотную характеристику данной цепи (ее комплексный коэффициент передачи) находим следующим образом:

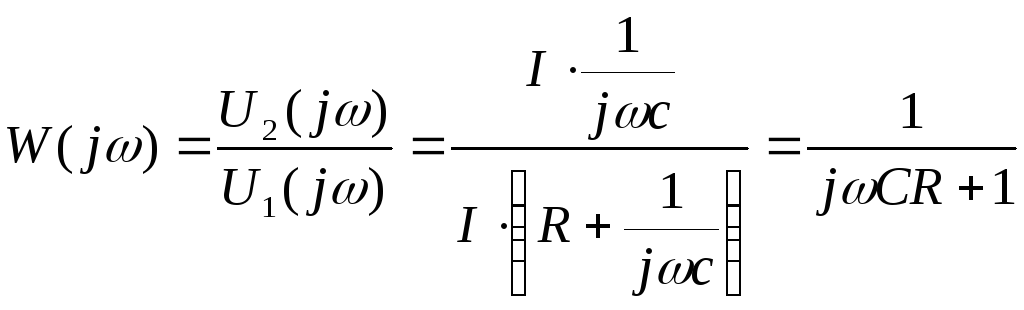(14.25)

3. Спектральную плотность выходного сигнала находим, подставляя (14.14) и (14.25) в (14.23)

4. Выходной сигнал получаем в результате обратного преобразования Фурье на основе выражения (14.22)

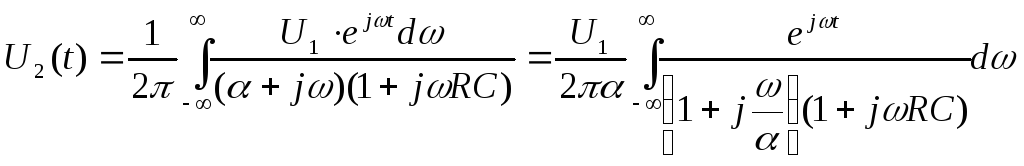(14.26)

Интеграл (14.26) табличный.

В итоге получаем

График функции (14.27) при приведен на (рис.14.3).

Рис. 14.3

Таким образом, переход от временных представлений сигналов к их частотным характеристикам значительно облегчает анализ цепей. Однако трудности могут возникнуть в следующих случаях:

- когда начальные условия не являются нулевыми;

• если сигналы не удовлетворяют условию квадратичной интегрируемости, т.е.

Эти проблемы снимаются при использовании операторного метода.