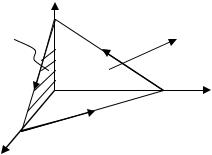
∫ x3dx −(y2 +5)dy +(x3 −2)dz = ∫∫(−3x2 )dxdz

L

σ

Перейдем от поверхностного интеграла к двойному, спроектировав поверхность σна плоскость Oxz . Тогда, учитывая, что нормаль к поверхности образует острый угол с осью Oy ,

получим

z
D 1		n
O	2	y
x
2	Рис. 1.31

			1	2−2 z					1	x	3			2−2 z
	∫∫(−3x2 )dxdz = −3∫∫ x2 dxdz = −3∫dz ∫				x2 dx = −3∫dz									=
										3
	σ	D	0	0					0					0
	= −8∫1 (1 − z )3 dz = 8∫1 (z −1)3 dz = 8					(z −1)4		1
									= −2.
	0		0			4		0

Замечание. При расстановке пределов в двойном интеграле использовалиограниченность области D сверху прямой x = 2 −2z .

Это уравнение получено из уравнения заданной плоскости при y = 0.

Вопросы для самопроверки по теме 1.3

1.Как определяется сторона поверхности?

2.Дайте определение поверхностного интеграла второго рода.

3.Напишите формулу связи поверхностных интегралов первого и второго родов.

4.Перечислите свойства поверхностных интегралов второго рода.

5.Напишите формулу Остроградского-Гаусса.

6.Напишите формулу Стокса.

Раздел 2. Теория поля

Данный раздел курса включает следующие темы:

2.1.Скалярное поле.

2.2.Векторное поле. Поток и циркуляция векторного поля.

2.3.Потенциальные и соленоидальные векторные поля.

2.4.Векторно-дифференциальные операторы I и II порядков.

В каждой теме сначала излагается теоретический материал и приводятся иллюстрирующие примеры. Завершает тему подробный разбор решений типовых примеров.

После каждой темы Вам следует ответить на вопросы для самопроверки. По завершении работы над разделом необходимо решить тест №2. Студенты очно-заочной и заочной форм обучения должны решить четыре задачи из контрольной работы № 8.

48

2.1. Скалярное поле

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Определение скалярного поля. Линии уровня.

•Производная по направлению.

•Градиент скалярного поля.

•Гармоническое поле.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [3] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить задачу под № 121-130 из контрольной работы № 8 в соответствии со своим вариантом.

Определение скалярного поля. Линии уровня

Если в каждой точке M некоторой области пространства (двумерного или трехмерного) задана функция U (M ) , то говорят, что в этой области

задано скалярное поле.

Если рассматриваемая область лежит на плоскости, то скалярное поле называется плоским, если в трехмерном пространстве, то скалярное поле называется пространственным. Примерами скалярных полей являются поле температур, поле потенциала.

Поле называется стационарным, если оно не изменяется во времени. Далее мы будем рассматривать только стационарное поле.

Приведем некоторые понятия, которые играют важную роль при изучении скалярных полей.

Линии уровня

Линия, во всех точках которой плоское скалярное поле F(M ) имеет одно и

то же значение, называется линией(равного) уровняскалярного поля.
Уравнение
U (x, y) = C	(2.1)

с переменным параметром C является уравнением семейства линий уровня плоского поля U (M ) . Известные из физики изотермы (линии равной

температуры), изобары (линии равного давления), эквипотенциальные линии (линии равного потенциала) являются примерами линий уровня в в соответствующих плоских скалярных полях.

Если значения	функции	U (M ) =U (x, y)	откладывать по оси
Oz : z =U (x, y), то	линиями	уровня скалярного	поля U (M ) =U (x, y)

будут проекции на плоскость Oxy линий, которые получаются в пересечении поверхности z =U (x, y) с плоскостями z = C. Здесь C должно принимать всё

49

множество	значений,	присваиваемых		z
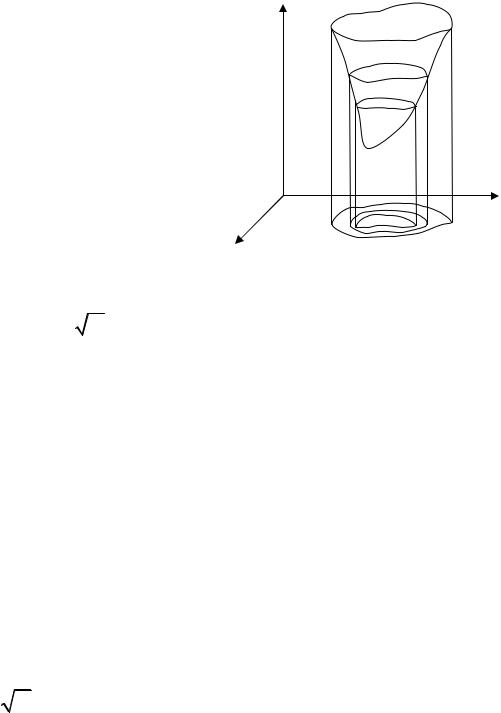
функцией U (M ); но на рисунке приводят
только часть линий (рис. 2.1).
Зная линии уровня, легко составить
представление о виде			поверхности
z =U (x, y).	Поэтому	задание линий
уровня, как и поверхности			z =U (x, y) ,
является	геометрическим		способом
представления функции U (M ) =U (x, y)
двух переменных.			x
Пример	2.1.	Для	плоского		Рис. 2.1
скалярного	поля	U (x, y) = x2 + y2
семейство линий уровня задается уравнением				x2 + y2	= C.	Это множество
окружностей с радиусом		C и центром в начале координат.				Очевидно, что
C ≥ 0. При C = 0 линия уровня вырождается в точку.					U (M ) =U (x, y, z).
Рассмотрим теперь пространственное скалярное поле
Для него уравнение		U (M ) =U (x, y, z) = C				(2.2)

определяет в пространстве Oxyz поверхность, во всех точках которой поле U (M ) имеет одно и то же значение.

Поверхность, во всех точках которой пространственное скалярное поле имеет одно и то же значение, называется поверхностью (равного) уровня этого поля.

Придавая в уравнении (2.2) параметру C различные значения из множества значений, принимаемых функцией U (M ) , получим семейство поверхностей

уровня поля U (M ) .

Пример 2.2. Для пространственного поля U (x, y, z) = x2 + y2 + z2 поверхности уровня определяются уравнением x2 + y2 + z2 = C. Это - семейство сфер с радиусом C и центром в начале координат при C > 0, и точка (0;0;0) , если C = 0.

Производная по направлению

Важной характеристикой скалярного поля является величина, показывающая, как быстро меняется поле в данном направлении.

Пусть задано скалярное поле U (M ) =U (x, y, z). Возьмем точку M и единичный вектор eG = (cos α, cosβ, cos γ) (координаты единичного вектора равны его направляющим косинусам). На линии действия вектора в направлении этого вектора возьмем точку M1.

50

Если при стремлении точки M

1

к точке M так, что точка M

1

остается на

линии

действия

G

отношения

вектора e ,

существует

конечный предел

U (M1 ) −U (M )

,

JJJJJG

то этот предел называется производной скалярного поля

MM1

U (M )

или функции u =U (M )

в точке M по направлению вектора e и

обозначается

∂UG .

Итак,

∂e

∂U

U (M

) −U (M )

∂eG

=

lim

1JJJJJG

.

(2.3)

M1 →M

MM1

Производную по направлению можно вычислить по формуле:

∂U	=	∂U cos α +	∂U cos β+	∂U cos γ.	(2.4)
∂e		∂x	∂y	∂z

Производная по направлению в плоском скалярном поле U (M ) =U (x, y) также вычисляется по формуле (2.4), в которой надо положить cos γ = 0, то есть

отбросить последнее слагаемое.
Пример 2.3. Найти производную функции U (x, y, z) = ln(x3			+ y2	+ z)	в
G	JJJJJG
точке M 0 (1;0;3) в направлении вектора a	= M0M1, если M1	(0;2;−1).

Решение. Найдем сначала единичный вектор e , задающий направление, по

которому надо определить производную.

Для

этого

находим вектор

JJJJJJG

−3) = (−1, 2, −4) или aG = −i +

2 Gj −

G

aG = M0M1

= (0 −1, 2 −0, −1

4k.

Тогда

−iG+ 2 Gj −4k

G

G

G

G

1

G

1

2

4

e =

G

|

a

=

= −

i

+

j −

k.

(−1)2

21

21

21

| a

+ 22 +(−4)2

Отсюда

1

2

4

cos α = −

,

cosβ =

,

cos γ = −

.

21

21

21

Далее находим частные производные функции U (x, y, z) :

∂U

=

3x2

,

∂U

=

2 y

,

∂U

=

1

.

∂x

x3

+ y2 + z

∂y

x3 + y2 + z

∂z

x3

+ y2 + z

Вычисляем значения их в точке M 0 (1;0;3)

∂F

=

3

,

∂F

= 0,

∂F

=

1

.

∂x

M0

4

∂y

M0

∂z

M0

4

51

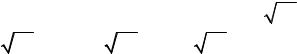
Записав формулу (2.4) в виде

∂U

∂U

∂U

∂U

∂eG

M0

=

∂x

M0

cos α +

∂y

M0

cos β+

∂z

M0

cos γ,

имеем

∂U

=

3

−

1

+

1

−

4

= −

7

= −

21

.

G

∂e

M0

4

21

4

21

4 21

12

Градиент скалярного поля

Определение. Градиентом скалярного поляU (M ) =U (x, y, z) в точке

M (x, y, z) называется вектор, координатами которого являются частные

производные ∂U ,

∂U ,

∂U

функции U (x, y, z)

в этой точке.

∂x

∂y

∂z

JJJJJG

Обозначается градиент символом gradU. Итак,

JJJJJJG

=

∂

G

∂

G

∂

G

(2.5)

gradU

U i

+ U j +

U k.

∂x

∂y

∂z

JJJJJG

В плоском скалярном поле U (M ) =U (x, y) вектор gradU определяется

равенством

JJJJJJG

∂

G

∂

G

gradU =

U

i

+

U j .

∂x

∂y

Пример 2.4. Дано скалярное поле U (M ) = x2 + y3z −3.

Найти градиент

полявточке M 0 (2;−1;−2).

Решение. Находим частные производные

∂U

= 2x,

∂U

= 3y2 z,

∂U

= y3.

∂x

∂z

∂y

Вычисляем их значения в точке M 0 (2;−1;−2)

∂U

= 4,

∂U

= −6,

∂U

= −8.

∂x

M0

∂y

M0

∂z

M0

JJJJJJJJJJJJG

∂

G

∂

G

∂

G

Записав формулу (2.5) в виде gradU

(M

0 ) =

U

i

+ U

j +

U

k ,

JJJJJJJJJJJJG

G

G

∂x

M0

∂y

M0

∂z

M0

имеем gradU (M0 )

= 4i

−6 j −8k.

52

Гармоническое поле
Если скалярное поле U (x, y, z) удовлетворяет уравнению
∂2U	+ ∂2U	+ ∂2U = 0	,	(2.6)
∂x2	∂y2	∂z2

то это поле называется гармоническим.

Плоское поле U(x, y) будет гармоническим, если оно удовлетворяет

уравнению ∂2U + ∂2U = 0 .

∂x2 ∂y2

Пример 2.5. Проверить, является ли скалярное поле U (x, y, z) = x2 z + xyz − y2 z +3 гармоническим.

Решение. Вычислим частные производные, входящие в уравнение

(2.6).
∂U	= 2xz + yz,					∂U = xz − 2 yz,		∂U = x2	+ xy − y2 .
∂x							∂y	∂z
Тогда
∂2U							∂2U	(xz −2 yz)′y = −2z,
∂x2	= (2xz + yz)′x = 2z, ∂y2 =
				∂2U			= (x2 + xy − y2 )′ = 0.
				2
				∂z				z
Следовательно,	∂2U	+	∂2U		+		∂2U = 2z −2z + 0 = 0.
	∂x2		∂y2				∂z2

Значит, поле U (x, y, z) удовлетворяет уравнению (2.6), т.е. является

гармоническим.

Решение задач

Задача 2.1. Найти линии уровня для плоского скалярного поля

U (x, y) = x2 − y2 .

Решение. В соответствии с формулой (2.1) линии уровня определяются уравнением x2 − y2 = C . Это семейство гипербол при C ≠ 0 и две прямые x = ±y (при C = 0).

Задача 2.2. Найти поверхности уровня для пространственного скалярного поля U (x, y, z) = x2 + y2 − z .

Решение. В соответствии с формулой (2.2) поверхности уровня определяются уравнением x2 + y2 − z = C или x2 + y2 = z +C . Эти

53

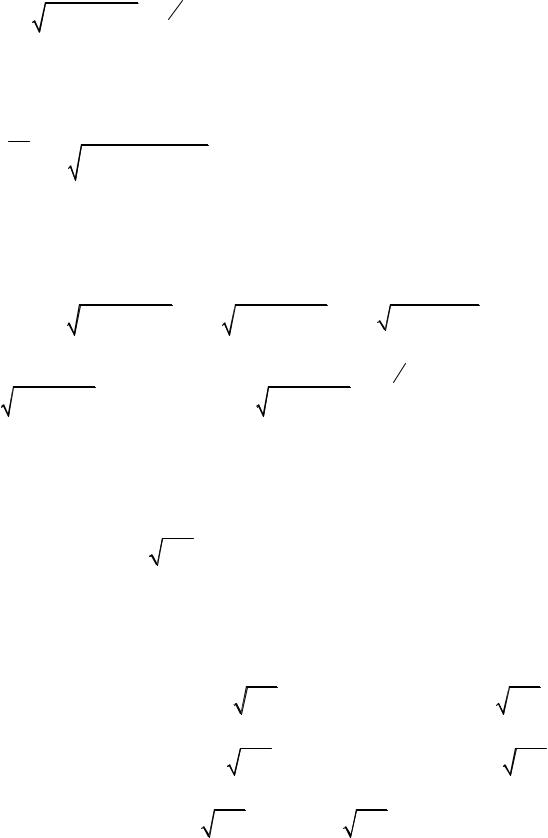
уравнения определяют семейство эллиптических параболоидов с вершинами

на оси Oz в точках (0;0; −C ).

Задача

2.3.

Найти

производную

скалярного

поля

U (x, y, z) =

x2

+ y2 − z −ez 2

в точке M 0 (3, 4,0)

по направлению вектора

G

G

G

G

a

= 2i − 4 j +

4k .

Решение. Найдем сначала единичный вектор e , задающий направление

вектора aG.

2 G

G

G

1 G

G

G

G

1

G

1

G

4

4

2

2

e =

G

a

=

a

=

6

i

−

6

j

+

6

k =

3

i −

3

j

+

3

k .

a

22 +(−4)2 + 42

Значит,

cos α =

1

; cos β = −

2

; cos γ =

2

.

Теперь

вычислим

частные

3

3

3

производные функции U (x, y, z)

в точке M0 .

∂U

=

2x

=

x

=

3

=

3

;

∂x

5

M0

2 x2 + y2 − z

M0

x2 + y2 − z

M0

32

+ 42 −0

∂U

y

4

∂U

−1

1

z

1

1

3

=

=

;

=

−

e

2

=−

−

=−

.

∂y

M

x2 + y2 −z

5

∂z

M0

2 x2 + y2 −z

2

10

2

5

M0

0

M

Тогда в соответствии с формулой (2.4) имеем

0

∂U

=

3

1

+

4

−

2

−

3

2

= −

11

.

G

∂e

M0

5

3

5

3

5

3

15

Задача 2.4. Найти градиент скалярного поля

U (x, y, z) = sin (x + 2 y)+

xyz : а) в произвольной точке M (x, y, z) ; б) в

π

3π

точке M0

;

;3

.

2

2

Решение.

Вычислим частные производные функции U (x, y, z) .

∂U

= cos(x + 2 y) (x + 2 y)′x

+

1

(xyz)′x

= cos(x + 2 y)+

yz

;

∂x

2

xyz

2

xyz

∂U

= cos(x + 2 y) (x + 2 y)′y +

1

(xyz)′y

=

2cos(x + 2 y)+

xz

;

∂y

xyz

2

xyz

2

∂U

= 0 +

1

(xyz)′z

=

xy

.

∂z

2

xyz

2

xyz

Тогда по формуле (2.5) получаем в производной точке M (x, y, z)

54

JJJJJJJJJJJG

yz

xz

xy

G

gradU(M) = cos(x +2y)+

iG

+ 2cos

(x +2y)+

Gj

+

k.

2

2

2 xyz

xyz

xyz

Для нахождения градиента в точке M0

подставим вместо x, y, z координаты

точки M0 :

JJJJJJJJJJJJG

π

9π

G

gradU

(M0 ) =

cos

2

+3π +

i

+

π

π

2 2

3

3

2

2

π

3π

G

3π2

G

3 G

1

G

π G

+

2 cos 2 +3π +

j

+

k

=

i

+

j + 4 k.

π

π

π

π

2

2

2 2

3

2 4

3

3

2

2

3

2

2

Задача 2.5. Проверить, будет ли скалярное поле U (x, y, z) = xz3 − x3 y

гармоническим.

Вычислим частные производные функции U (x, y, z)

Решение.

сначала

первого, и потом второго порядка.

∂U

= z3 −

3

x y;

∂U

= − x3

1

;

∂U = 3xz2 ;

∂x

2

∂y

y

2

∂z

∂2U

= −

3 y

;

∂2U

=

x3

;

∂2U

= 6xz .

∂x2

4 x

∂y2

∂z2

4 y3

Тогда

∂2U

+ ∂2U

+ ∂2U

= −

3

y

+

x3

+ 6xz ≠ 0.

∂x2

4 x

4 y3

∂y2

∂z2

Значит, поле U (x, y, z) не будет гармоническим.

Вопросы для самопроверки по теме 2.1

1.Дайте определение скалярного поля.

2.Дайте определение линии уровня и поверхности уровня.

3.Дайте определение производной по направлению.

4.Напишите формулу для вычисления производной по направлению.

5.Что такое градиент скалярного поля?

6.Какое скалярное поле называется гармоническим?

55

2.2. Векторное поле. Поток и циркуляция векторного поля

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Векторное поле. Основные понятия.

•Поток векторного поля.

•Дивергенция векторного поля. Теорема Остроградского-Гаусса в векторной форме.

•Циркуляция и ротор векторного поля. Теорема Стокса в векторной форме.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить две задачи под № 131-150 из контрольной работы № 8 в соответствии со своим вариантом.

Векторное поле. Основные понятия

Аналогично понятию скалярного поля вводится понятие векторного поля. А именно, если в каждой точке M некоторой пространственной области определена векторная величина, то, говорят, что в этой области задано векторное поле. Примерами векторных полей в физике могут служить силовое поле, поле скоростей точек твердого тела, электромагнитное поле.

Поле называется стационарным, если оно не изменяется во времени. Мы далее будем рассматривать только стационарные векторные поля.

G Если область, в которой задано векторное поле, - плоскаяG и все векторы a (M ) лежат в этой же плоскости, то векторное поле a (M ) называется плоским.

Если в пространстве имеется прямоугольная декартова система
координат Oxyz , то векторное поле a (M )= aG	(x, y, z) можно задавать его
координатами в этой системе, т.е.	Gj + az (x, y, z)kG.
aG(x, y, z)= ax (x, y, z)i + ay (x, y, z)		(2.7)

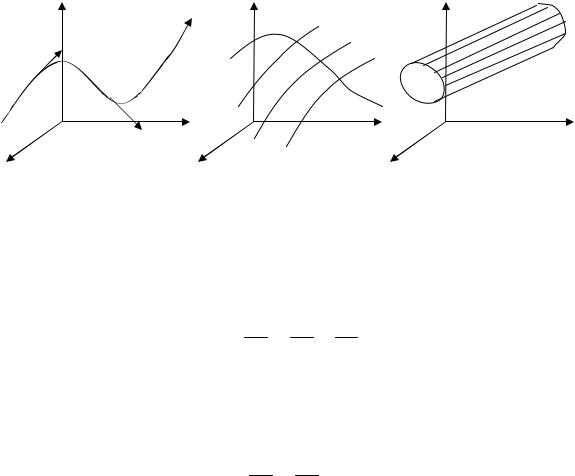
Приведем некоторые понятия, которые играют важную роль при изучении векторного поля. Векторной линией поля a называется линия, для которой в каждой ее точке М вектор a (M ) является ее касательным вектором

(рис. 2.2)

Если через каждую точкуG некоторой кривой l проходит некоторая векторная линия L поля a , то поверхность, составленнаGя из всех этих векторных линий, называется векторной поверхностью поля a (рис. 2.3).

Если кривая l - замкнутая, то векторная поверхность в этом случае называется векторной трубкой (рис. 8.4).

56

L , то они

(2.8)

z	L	z		z
aG		l
	aG
O		O	l	O
x	y	y	x	y
	x
	Рис. 2.2	Рис. 2.3		Рис. 2.4

Примерами векторных линий могут служить линии тока жидкости в поле линейных скоростей частиц стационарного потока жидкости или магнитные силовые линии в магнитном поле.

Если x, y, z - координаты точки M векторной линии

удовлетворяют уравнениям:

dx = dy = dz , ax ay az

которые называются дифференциальными уравнениями векторныхG линий.G

В случае плоского векторного поля a(x, y) = ax (x, y)i + ay (x, y) j система уравнений (2.8) примет вид:

dx = dy . ax ay

Пример 2.6. Найти векторные линии поля a = xy2i + x2 yjG. Решение. Запишем дифференциальное уравнение векторных линий:

			dx	=	dy
	xdx = ydy .Это		xy2		x2 y
или		дифференциальное					уравнение с разделенными
переменными. Интегрируя его, получаем
	C - произвольная	x2 − y2 = C ,
где		постоянная.		Таким			образом, векторными линиями

данного поля aG являются равнобочные гиперболы x2 − y2 = C .

Поток векторного поля

Понятие потока векторного поля возникает при решении задачи о расчете количества жидкости, протекающей через заданную поверхность, при решении задачи о потоке тепла через поверхность и ряде других физических задач.

57

Определение потока векторного поля

Потоком П векторного поля a через двустороннюю поверхность σ в

выбранную сторону называется поверхностный интеграл
	∫∫andσ,	(2.9)
	σ
где an - проекция поля a на единичную нормаль к поверхности σ ,
направление	которой соответствует выбранной стороне	поверхности, т.е.
an = aG nG.	нормаль единичная, то nG = cos αi +cos βGj +cos γkG, где α,β, γ -
Так как nG -

углы, образованные вектором n с осями Ox,Oy,Oz соответственно. Тогда

aG nG

= ax cos α + ay cos β+ az cos γ, и, следовательно,

z

)

П =

∫∫

n

∫∫(

a

x

cos

α + a

y

cos β+ a

(2.10)

a dσ =

cos γ dσ.

σ

σ

Если поверхность σ задается уравнением z = z (x, y), то направляющие

косинусы нормали вычисляются по формулам

−z′y

−z′

,

,

cos α =

x

cos β =

± 1 + (z′x )2 + (z′y )2

± 1 + (z′x )2 + (z′y )2

cos γ =

1

.

(2.11)

± 1 + (z′x )2 + (z′y )2

Знаки перед радикалами выбираются так, чтобы направление нормали

соответствовало выбранной стороне поверхности.

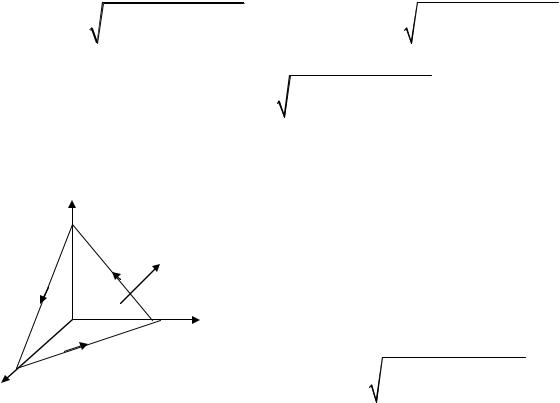
Пример

2.7.

Вычислить

поток

2

z

векторного поля aG = yi + xjG+ zkG через часть

nG

плоскости

2x + 2 y + z = 2 ,

лежащую

в

первом октанте, в направлении нормали,

образующейострыйуголсосью Oz (рис. 2.5).

σ O

B

y

Решение. Спроектируем поверхность σ

на

плоскость

Oxy и

перейдем в

интеграле

1

1

(2.10)

от

поверхностного к

двойному.

При

Рис. 2.5

1+(z′x )2 +(z′y )2 dxdy ,

x

A

этом

dσ =

а

направляющие косинусы заменяем по формулам (2.11), причем перед радикалами выбираем знак "+", так как в условии задачи сказано, что n образует с осью Oz острый угол и, значит, cos γ > 0 . Таким образом,

П = ∫∫(ax (−z′x )+ ay (−z′y )+ az )dxdy ,

(2.12)

D

58

где D - проекция σ на плоскость Oxy , т.е. треугольник AOB ; ax , ay , az -
координаты векторного поля aG, причем переменная z заменена на z (x, y)							из
уравнения поверхности, т.е. ax = y, ay = x, az					= z = 2 − 2x − 2 y .		z′y :
Выразим из	уравнения плоскости			z	и вычислим z′x	и
z = 2 − 2x − 2 y, z′x = −2, z′y = −2.
Подставляя в формулу (2.12), получаем
П = ∫∫	(y 2 + x 2 + 2 − 2x − 2 y)dxdy = 2∫∫dxdy .
D					D	AOB и,
Последний интеграл представляет собой площадь треугольника
следовательно,		1
	П = 2		1 1	=1.
	2
	Дивергенция векторного поля.
Теорема Остроградского-Гаусса в векторной форме

Пусть поверхность σ - замкнутая, ограничивающая тело T , объем

	которого обозначим через V .
	В этом случае П = ∫∫andσ называется обильностью поля aG в теле T .
	σ
	ЕслиGÏ > 0 , то говорят, что в теле V есть источники; если Ï < 0
	- то стоки поля a .
	Тогда отношение	∫∫andσ
	Ï
		= σ
	V	V

можно рассматривать как среднюю плотность источников и стоков, распределенных в теле T .

Зафиксируем теперь внутри поверхности σ некоторую точку M . Обозначим через λ диаметр области T и будем стягивать поверхность σ к точке M , устремляя λ к нулю. Если при этом существует конечный предел указанного отношенияG, то он называется дивергенцией поля a в точке M и обозначается так: div a (M ) или div a , т.е.

	div aG(M )= lim		∫∫andσ
			σ		.
			V
		λ→0
Можно	доказать,	что,			если	координаты
ax (x, y, z),	ay (x, y, z), az (x, y, z)	вектора		a (x, y, z)		непрерывны в
		59

z =1.

области T и имеют непрерывные частные производные

∂a

x

,

∂ay

,

∂a

z

, то

∂y

M области

T дивергенция

∂x

∂z

для любой точки

существует

и

может быть

вычислена по формуле

∂ay

G

(M )=

∂a

x

∂a

z .

div a

+

+

(2.13)

∂y

∂x

∂z

Обратимся теперь к формуле Остроградского-Гаусса. Положив в ней

P = ax , Q = ay ,

R = az , можем написать

G

∫∫∫div adxdydz =∫∫axdydz +aydxdz + azdxdy .

T

σ

Далее воспользуемся формулой перехода от поверхностного интеграла

второго рода к интегралу первого рода. Тогда

∫∫∫

G

∫∫(

x

y

z

)

∫∫

n

divadxdydz =

a

cos α + a

cos

β+ a

T

cos γ dσ =

a dσ.

σ

σ

Таким образом, теорему Остроградского-Гаусса можно сформулировать в векторной форме.

Поток векторного поля a через замкнутую поверхность σ в сторону внешней нормали равен тройному интегралу от дивергенции этого поля по телу T , ограниченному поверхностью σ, т.е.

П = ∫∫andσ = ∫∫∫divadxdydz .		(2.14)
σ	T

Пример 2.8. Найти с помощью теоремы Остроградского-Гаусса поток векторного поля aG = (x3 +1)iG+(y3 +1)Gj + 2k через поверхность тела,

ограниченного конусом x2 + y2 = z2 и плоскостью

Решение. Вычислим дивергенцию поля a , используя формулу (2.13):

div aG = ∂∂x (x3 +1)+ ∂∂y (y3 +1)+ ∂∂z (2)= 3x2 +3y2 .

Всоответствии с формулой (2.14) имеем

П= ∫∫∫3(x2 + y2 )dxdydz .

T

Вычислим тройной интеграл, переходя к цилиндрическим координатам:

			2π		1			1
П = 3∫∫∫ρ2ρdϕdρdz = 3 ∫				dϕ∫		ρ3dρ∫dz =
		T	0		0			ρ
2π	1	ρ3	2π		ρ4		−	ρ5			1	3π	.
= 3 ∫ dϕ∫			(1−ρ)dρ = 3 ∫ dϕ		4			5			=	10
0	0		0
											0
			60

Циркуляция и ротор векторного поля. Теорема Стокса в векторной форме

	Пусть в некоторой области T задано векторное поле
	aG(x, y, z)= ax (x, y, z)i + ay (x, y, z) Gj +az (x, y, z)kG.
Пусть далее l - кривая, лежащая в области T .
	Интеграл ∫axdx +aydy + azdz называется линейным интегралом поля
aG	l
	по кривой l . Этот интеграл иногда обозначают так: ∫al dl .

l

GЕсли кривая l - замкнутая, то такой интеграл называется циркуляцией поля a вдоль кривой l

c = ∫al dl

G l

Если поле a - силовое поле, то линейный интеграл выражает работу сил поля при перемещении точки единичной массы по кривой l .

Пусть в области T задана гладкая двусторонняя поверхность σ, ограниченная замкнутым контуром l . Тогда, используя формулу Стокса и формулу перехода от поверхностного интеграла второго рода к интегралу первого рода, можно вычислить циркуляцию C так:

C =

a dl =

∂az −

∂ay

dydz +

∂ax −

∂az dxdz +

∂ay

−

∂ax

dxdy =

∫

∫∫

l

∂y

∂z

∂z

∂x

∂x

∂y

l

σ

=

∂az −

∂ay

cos α+

∂ax − ∂az

cos β+

∂ay

−

∂ax

cos γ

dσ.(2.15)

∫∫

∂y

∂z

∂z

∂x

∂x

∂y

σ

Последний интеграл Gравен потоку векторного поля, которая называется

ротором или вихрем поля a и обозначается символом

JJG

G

∂az

∂a

y

G

∂

∂az

G

∂a

y

∂

G

ax

ax

rota

=

−

i +

−

j

+

−

k .

(2.16)

∂y

∂z

∂z

∂x

∂x

∂y

Тогда равенство (2.15) можно записать в виде

JG

∫al dl = ∫∫(rotaG)

dσ.

(2.17)

l

σ

n

Таким образом, теорему СтоксаG можно сформулировать в векторной форме. Циркуляция поля a вдоль замкнутого контура l равна потоку ротора этого поля через поверхность σ, ограниченную контуром l . При этом сторона

поверхности и направление обхода должны соответствовать друг другу.

61

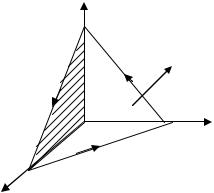
z

Пример 2.9. Вычислить, используя

теорему

Стокса,

циркуляцию

поля

2

C

G

aG = (x +1)i + yjG

+ z (1− x)kG

по

линии

ABCA пересечения плоскости x + y + z = 2

σ

n

с

координатными

плоскостями.

Точки

2

y

A, B,C -

точки

пересечения

плоскости с

B

осями Ox,Oy,Oz соответственно.

2

Решение. Вычислим сначала частные

Рис. 2.6

x A

производные, участвующие в определении

ротора (2.16).

∂a

x

= 0,

∂a

x

=

0,

∂ay

= 0,

∂ay

= 0,

∂a

z

= −z,

∂a

z

= 0.

∂x

∂z

∂y

JJG

∂z

∂x

∂y

= zjG,

JG

Тогда

rotaG

и, значит,

(rotaG)n = (zj )n = z cosβ. Используя

формулу Стокса (2.17), получаем

C = ∫al dl = ∫∫ z cos βdσ.

(2.18)

lσ

Вкачестве поверхности σ берем плоскость x + y + z = 2. Заметим, что

заданному направлению обхода контура соответствует нормаль, образующая острый угол с осью Oy , т.е. cosβ > 0. Перейдем от поверхностного интеграла

в равенстве (2.18) к двойному, проектируя поверхность σ на плоскость Oxz

(проекция D на рис. 2.6 заштрихована).

Так как

cosβ > 0,

то

cos βdσ

заменим на dxdz . Вычислим двойной интеграл:

2 2−x

1

2

2

1

3

2

4

C = ∫∫ zdxdz = ∫dx ∫ zdz

=

∫(2 − x)

dx = −

(2

− x)

=

.

2

6

0

3

D

0

0

0

Примечание. Вычисление ротора векторного поля

Ротор векторного поля aG (2.16) удобно вычислять, используя формулу

JJGG

iG

Gj

k

∂

∂

∂

rota =

.

(2.19)

∂x

∂y

∂z

ax

ay

az

Этот определитель вычисляется по обычным правилам вычисления

определителей, только формальное умножение любого из символов

∂

,

∂

,

∂

∂x

∂y

∂z

на f (x, y, z) надо понимать, как взятие частной производной.

62

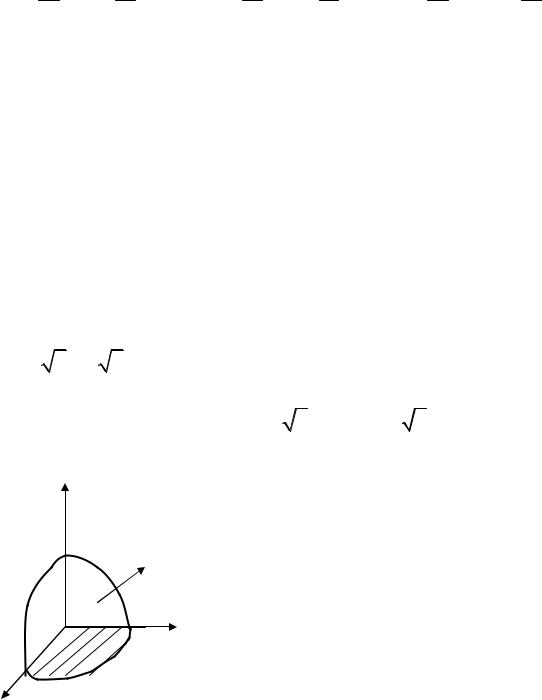
Пример 2.10. Вычислить ротор векторного поля aG = yzi +(x + z) Gj +3yk .

Решение. Воспользуемся формулой (8.19). Вычислять определитель будем, раскладывая его по первой строке,

JJGG

iG

Gj

kG

G

∂

∂

G

∂

∂

G

∂

∂

∂

∂

∂

∂y

∂z

∂x

∂y

rota

=

= i

− j

∂

∂

+ k

=

∂x

∂y

∂z

x

z

x + y

3y

yz

3y

yz x + z

yz

x + y

3y

=iG ∂∂y (3y)−∂∂z (x +z) − Gj ∂∂x (3y)−∂∂z (yz) +kG ∂∂x (x +z)−∂∂y (yz) =

=iG(3−1)− Gj (0 − y)+kG(1−z)=2iG+ yjG+(1−z)kG.

Решение задач

Задача 2.6. Найти поток векторного поля	a = 2 j через часть плоскости
2x + z = 6, ограниченную координатными	плоскостями, и плоскостью
y = 3 в направлении нормали, образующей тупой угол с осью Ox .

Решение. Для вычисления потока воспользуемся формулой (2.10), вычислив предварительно an . Так как рассматриваемая поверхность -

плоскость, то коэффициентами перед переменными являются координаты

нормали

к ней,

т.е. NG

= (2; 0;1). Соответственно

единичная нормаль

G

2

1

n

=

; 0;

. Тогда

5

5

a = aG nG = 0

2

1

+ 2 0 +0

= 0.

n

5

5

z

9 nG

O

1 y

x 3

Рис. 2.7

Следовательно,

П = ∫∫Odσ = 0.

σ
Задача 2.7.	Найти		поток	векторного поля
aG = 9 yzi − xzjG	+8xyk		через	часть поверхности
σ: 9 y2 + x2 = 9 − z ,		лежащую в первом октанте
(x ≥ 0; y ≥ 0, z ≥ 0)		в	направлении нормали,

образующей острый угол с осью Oz .

Решение. Для вычисления потока будем использовать формулу (2.12), вычислив

63

предварительно величины, входящие в нее.

		Выразим z из уравнения поверхности:																	z = 9 −9 y2 − x2 . Тогда
	z′x = −2x, z′y		= −18y ,
ax = 9 yz = 9 y(9 −9 y2 − x2 ),														ay = −xz = −x(9 −9 y2 − x2 ),																				az = 8xy .
Тогда в соответствии с формулой (8.12) получаем
П = ∫∫ 9 y (9 −9 y					− x		) 2x − x(9 −9 y											− x			) 18 y +8xy dxdy = ∫∫8xydxdy.
				2		2											2			2
		D																																D
		Область D , проекция рассматриваемой части поверхности σ на
плоскость Oxy ( на рис. 2.7 заштрихована), ограничена осями координат и
кривой, уравнение которой									y =			1		9 − x2				получено из уравнения поверхности
											3
									1	при z = 0 . Тогда
						3					9 − x			2							3					1
									3																		9 − x			2
		∫∫8 xyd xd y = 8 ∫d x									∫			xyd y = 4 ∫d x xy 2												03						=
		D				0					0										0
	4	3						4	3													4		9 x	2			x	4					3
=		∫ x (9 − x 2	)d x =						∫(9 x − x 3 )d x =																	−								= 9 .
							9														9			2			4
9		0							0																									0
	Задача 2.8. Вычислить с помощью теоремы Остроградского-Гаусса поток
векторного поля				G		G				2	G			3z	2	k	в		сторону					внешней							нормали через
			a		= yi			+ xz			j +

полную поверхность σ тела, лежащего в первом октанте (x ≥ 0; y ≥ 0, z ≥ 0),

и

ограниченного

поверхностью S : x +5y + 2z =10

и

координатными

плоскостями.

Решение.

Вычислим

дивергенцию

z

векторного поля, используя формулу (8.13).

5

G

∂a

x

∂ay

∂a

z =

diva

=

+

+

G

∂y

∂x

∂z

n

+(xz2 )′ +(3z2 )′ = 6z.

2

y

= (y)′x

O

y

z

Тогда в соответствии с формулой (2.14)

10

Рис. 2.8

П = ∫∫∫6zdxdydz .

x

T

Перейдем от тройного интеграла к повторному, используявидобласти T (рис. 2.8).

64

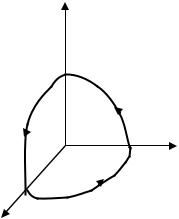
1

(10−x−5 y)

10

1

(10−x)

2

5

1

∫∫∫6zdxdydz = ∫∫dxdy

∫

6zdz = ∫dx

∫

dy3z2

02(10−x−5 y) =

T

D

0

0

0

1

(10−x)

1

(10−x)

3

10∫dx5

−3

10∫dx5

=

∫

(10 − x −5y)2 dy =

∫ (10 − x −5y)2 d (−5y −x +10)=

4 0

0

5 4 0

0

=−

3

10∫dx

(10−x−5y)3

15(10−x)

=

1

10∫(10−x)3 dx =−

1 (10−x)4

10

=

104

=53 =125.

20 0

3

0

20 0

20

4

0

20 4

Задача 2.9. Вычислить, используя определение, циркуляцию векторного

G

G

+15y

2

G

G

по линии

ABFA пересечения с координатными

поля a = yzi

z j

−3xk

плоскостями

части

поверхности

σ:

x2 + 4 y2

= 4 − z , лежащей в первом

октанте, ABF - точки пересечения поверхности с осями Ox,Oy,Oz

соответственно.

Решение. Рассматриваемая кривая изображена на рис. 2.9. Используя определение циркуляции и свойство аддитивности криволинейного интеграла, получаем

C = ∫	yzdx +15y2zdy −3xdz = ∫ yzdx+15y2 zdy −3xdz + ∫ yzdx +15y2zdy −3xdz +
ABFA	AB	BF

+∫ yzdx+15y2 zdy −3xdz =CAB +CBF +CFA.

FA

Вычислим отдельно каждый из трех интегралов.

z

1) На дуге

AB

z ≡ 0

и

dz = 0,

поэтому

CAB = ∫0dx +0dy = 0.

4

F

2) Дуга BF является частью параболы 4 y2

= 4 − z ,

а y меняется от 1

до 0.

Учитывая, что

x = 0 и

O

B

dx = 0 , получаем

0

(4 −4 y2 )dy =

y

CBF = ∫15y2 zdy = ∫15 y2

A

1

BF

1

0

x 2

Рис. 2.9

y3

y5

= 60

−

= −8.

3

5

1

3) Дуга FA - часть параболы x2 = 4 − z ,

x меняется от 0 до 2. Учитывая, что

y = 0 и dy = 0 , получаем

65

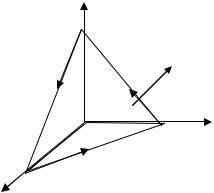
CFA = −∫3xdz = −∫2

3x (4 − x2 )′ dx =6∫2

x2dx =6

x3

2

=

16.

FA

0

0

3

0= 8.

Суммируя полученные результаты, получаем

C = 0 −8 +16

z

Задача

8.10.

Используя

теорему

Стокса, вычислить циркуляцию векторного

5

F

поля aG = 3xyi +3yjG+3zk по линии ABFA,

nG

линии пересечения

с

координатными

плоскостями

той

части

поверхности σ :

x +5y + 2z =10,

которая

лежит

в первом

2

y

октанте;

A, B, F

-

точки

пересечения

10

D

B

поверхности

σ

с

осями

Ox,Oy,Oz

соответственно (рис. 2.10).JJGG

x

A

Рис. 2.10

Решение. Вычислим rota , используя

формулуG(2.19):

JJGG

i

j

k

∂

∂

∂

rota =

=

∂x

∂y

∂z

3xy

3y

3z

G

∂

∂

G ∂

∂

G

∂

∂

= i

(3z)−

(3y) − j

(3z)−

(3xy)

+ k

(3y)−

(3xy) =

∂y

∂z

∂z

∂y

∂x

∂x

JJG

= iG(0 −0)− Gj

(0 −0)+ kG(0 −3x)= −3xkG.

= (

G

Тогда

(rotaG)n

−3xk )n

= −3x cos γ,

и в соответствии с формулой Стокса

(2.17) получаем

C = −∫∫3x cos γdσ.

σ

В качестве поверхности

σ берем плоскость

x +5y + 2z =10

. Заданному

направлению

обхода контура

ABFA соответствует нормаль, образующая

острый угол с осью Oz . Следовательно,

C = −∫∫3x cos γdσ = −∫∫3xdxdy = −∫∫3xdxdy ,

σ

σ

D

где D - проекция σ на плоскость Oxy . Используя вид области D (рис. 2.10),

перейдем к повторному интегралу и вычислим его.

66

		10	1	(10−x)					10			1							10
			5															3
C = −3∫∫xdxdy = −3∫dx				∫			xdy = −3∫dx xy							05(10−x) = −					∫x(10 − x)dx =
																		5
D		0		0					0										0
	3	10			2			3		2		x3					10
= −		(10x − x				)dx = −			5x		−						= −100.
	5	∫0						5				3					0

Вопросы для самопроверки по теме 2.2

1.Что такое векторное поле?

2.Дайте определение векторной линии, векторной поверхности.

3.Какая физическая задача приводит к понятию потока векторного поля?

4.Дайте определение потока векторного поля через заданную поверхность.

5.Что такое дивергенция векторного поля?

6.Сформулируйте теорему Остроградского-Гаусса в векторной форме.

7.Дайте определение циркуляции и ротора векторного поля.

8.Сформулируйте теорему Стокса в векторной форме.

2.3. Потенциальные и соленоидальные векторные поля

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Потенциальное векторное поле.

•Соленоидальное векторное поле.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить задачу под № 151-160 из контрольной работы № 8 в соответствии со своим вариантом.

Потенциальное векторное поле

Векторное поле aG называется потенциальным, если существует

скалярное поле U , для которого a служит градиентом, т.е.
	G	JJJJJG
	a	= gradU .
Напомним, что это равенство означает, что
ax = ∂U	, ay	= ∂U , az =	∂U .	(2.20)
∂x		∂y	∂z

Это скалярное поле U называется потенциалом (потенциальной функцией, скалярным потенциалом) поля a . Примерами потенциальных полей могут служить электрическое поле точечного заряда, поле тяготения,

67

магнитное поле, созданное прямолинейным проводником, по которому течет постоянный электрический ток.

НеобходимоеGи достаточное условие потенциальности векторного поля: чтобы поле a было потенциальным, необходимо и достаточно, чтобы в

каждой точке ротор a равнялся нулю, т.е.
JGG	= 0	(2.21)
rota

Поэтому потенциальное векторное поле называют также безвихревым.

Основные свойства потенциального поля:

1. Циркуляция потенциального поля по любому кусочно-гладкому замкнутому контуру равна нулю.

2. Линейный интеграл от потенциального поля по кусочно-гладкому

пути не зависит от путиG.

Потенциал поля a можно найти по формулам

(x, y,z)

U (x, y, z)=

∫

ax (x, y, z)dx +ay (x, y, z)dy +az (x, y, z)dz +C

(2.22)

или

(x0 , y0 ,z0 )

U (x, y, z)= ∫x ax (x, y0, z0 )dx + ∫y ay (x, y, z0 )dy + ∫z az (x, y, z)dz +C,

(2.23)

x0

y0

z0

где (x0 , y0 , z0 )

- некоторая фиксированная точка в рассматриваемой области,

C - произвольная постоянная.

aG = (y +cos z)iG+ xjG− x sin zk

Пример

2.11.

Показать,

что

поле

потенциально во всем пространстве и найти его потенциал.

JJGG

Решение. Вычислим rota , используя формулу (2.19):

iG

Gj

kG

= iG(0 −0)− Gj (−sin z +sin z)+(1−1)kG = 0G,

rotaG =

∂

∂

∂

∂x

∂y

∂z

y +cos z

x

−xsin z

т.е. поле

aG

потенциально во всем пространстве. Для нахождения потенциала

воспользуемся формулой (2.23), а в качестве точки (x0 , y0 , z0 )

возьмем начало

координат.

x

y

z

x

y

z

U (x, y, z)

= ∫

(0 + cos 0)dx + ∫ xdy −

∫xsin zdz = ∫dx + x∫dy

− x∫sin zdz +C =

0

0

0

0

0

0

= x

x

+ xy

y

+ x cos z

z +C = x + xy + x cos z − x cos 0 +C =

0

0

0

= x

+ xy + x cos z − x +C = xy + x cos z +C.

68

Соленоидальное векторное поле

Векторное поле aG называется соленоидальным, или трубчатым, если
существует векторное поле bG	, для которого a является ротором:
	aG = rotb .	(2.24)

поля aGВекторное. поле bG в этом случае называется векторным потенциалом

Необходимое и достаточноеG условие соленоидальности поля:

для того чтобы поле a было соленоидальным, необходимо и достаточно, чтобы во всей рассматриваемой области выполнялось равенство

diva = 0 .

(2.25)

Основные свойства соленоидального поля:

1. Поток соленоидального поля через любую замкнутую поверхность равен нулю.

2. Поток соленоидального поля через любую незамкнутую поверхность, опирающуюся на один и тот же замкнутый контур имеет одно и то же значение.

3. Поток соленоидального поля через любое сечение заданной векторной трубки этого поля имеет постоянное значение. Это значение называют

интенсивностью векторной трубки.
Поле aG	называется гармоническим, или лапласовым, если оно
одновременно является и потенциальным и соленоидальным.
						Решение задач
Задача 2.11. Показать, что скалярное поле U (x, y, z) = 2xyz + y2 +C
является потенциалом векторного поля aG = 2 yzi + 2 (xz + y)								Gj + 2xykG.
Решение.	Покажем, что a = gradU , т.е., что выполняются равенства
(2.20).		∂U				(2xyz + y2 +C )′
					=		= 2 yz = ax ,
		∂x
							x
		∂U			=	(2xyz + y2 +C )′	= 2xz + 2 y = ay ,
		∂y
							y
			∂U			= (2xyz + y2 +C )′ = 2xy = az .
				∂z
							z	z G	3 G
							G			z	k
Задача 2.12. Показать, что векторное поле a = e i −4 y									j	+ xe

потенциально и найти его потенциал.

Решение. Для доказательства потенциальности поля вычислим rota и воспользуемся формулой (2.21).

69

iG

Gj

kG

G

G ∂

G

∂

∂

∂

∂

z

∂

3

z

∂

z

rota =

= i

(xe

)−

(−4 y

) −

j

xe

−

(e

)

+

∂x

∂y

∂z

∂y

∂z

∂z

∂x

ez

−4 y3

xez

G

∂

∂

G

G

G

G

+k

(−4 y3 )

−

(ez )

= (0 −0)i −(ez −ez ) j

+(0 −0)k

=

0.

∂Gx

∂y

Значит, поле a потенциально.

Для нахождения потенциала U (x, y, z) воспользуемся формулой (2.23), а

в качестве точки (x0 ; y0 ; z0 )

возьмем точку (0;0;0).

x

y

z

x

y

z

U (x, y, z)= ∫e0dx −

∫4 y3dy +

∫ xez

= ∫dx −4∫ y3dy + x∫ez dz

+C =

0

0

0

0

0

0

= x

x

−y4

y + xez

z +C = x − y4 + xez − xe0 +C = xez − y4 +C.

0

0

0

G

Задача

G

2.13.

Проверить,

будет

ли

векторное

поле

= (y

2

− z

2

G

2xz +1)k соленоидальным.

a

)i

+ 2xyj −(

Решение.

Проверим, выполняется ли равенство (2.25).

divaG =

∂

(y2

− z2 )+

∂

(2xy)+

∂

(−2xz −1)= 0 + 2x −2x = 0.

∂x

∂z

∂y

Значит, поле a соленоидально.

G

Задача

G

2.14.

Проверить,

будет

ли

векторное

поле

= (e

y

+ ze

x

+ xe

y G

+e

x

G

a

)i

j

k гармоническим?

Решение. Векторное поле a является гармоническимG , если оно одновременно соленоидально и потенциально. Вычислим diva

divaG = (ey + zex )′x +(xey )′y +(ex )′z = zex + xey +0 ≠ 0.

Значит, поле не является соленоидальным, и, следовательно, не является гармоническим.

Вопросы для самопроверки по теме 2.3

1.Дайте определение потенциального и соленоидального векторных полей.

2.Сформулируйте признаки потенциальности и соленоидальности векторных полей.

3.Перечислите свойства потенциальных векторных полей.

4.Перечислите свойства соленоидальных векторных полей.

5.Какое поле называется гармоническим?

70

2.4. Векторно-дифференциальные операторы I и II порядков

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Оператор Гамильтона. Оператор Лапласа.

•Векторно-дифференциальные операции первого и второго порядков.

После изучения данных вопросов в опорном конспекте Вам следует ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию.

Оператор Гамильтона. Оператор Лапласа.

Операции получения градиента, дивергенции и ротора можно записать более просто, если ввести в рассмотрение (чисто формально) символический вектор

G	∂		G		∂	G		∂ G
=		i		+		j	+		k .	(2.26)
	∂x				∂y			∂z
G				Этот			вектор			называется оператором
Символ читается "набла".

Гамильтона или набла-вектором. При этом формальное умножение любого из

	символов	∂	,	∂	или	∂	на скаляр надо понимать, как взятие частной
		∂x		∂y		∂z

производной по соответствующей переменной (мы об этом говорили, когда вычисляли ротор). Например,

G

∂

G

∂

G

∂

G

∂

G

∂

G

∂

G

U (x, y, z)=

i

+

j +

k U =

Ui

+

Uj

+

Uk

=

∂x

∂y

∂z

∂x

∂y

∂z

G

=

∂U G

+

∂U

G

+

∂U

= gradU .

∂x

i

∂y

j

∂z

k

Работая с вектором формально как с вектором, только заменяя произведение

на взятие

частной

производной, можно

вычислить скалярное

и

векторное

G

произведение вектора на вектор a . Тогда получим

G

∂

G

∂

G

∂

G

G

G

G

∂

∂a

y

aG

=

i +

j +

k

(axi

+ ay j

+ azk )=

ax +

+

∂az

= divaG,

∂y

∂z

∂x

iG

Gj

∂x

∂y

∂z

k

G

G

∂

∂

∂

G

× a

=

= rota .

∂x

∂y

∂z

ax

a y

az

В.Гамильтон (1805-1856) - английский физик и математик.

71

Операции получения градиента, дивергенции и ротора называются

векторно-дифференциальными операциями первого порядка, так как при этом используются частные производные первого порядка.

При действиях с оператором надо пользоваться правилами векторной

алгебры и правилами дифференцирования. Например,

G

G

(

G

)

G

(

G

G

G

G

G

G

rot

a +b

G

a

+b

) G

+ ×b

= rota + rotb ,

= ×

= ×a

grad (λU )

= (λU )= λ U = λgradU

(λ = const ).

После применения оператора (2.26) к векторному или скалярному полю мы получаем новое поле, к которому опять можно применить этот оператор. Применение двух векторно-дифференциальных операций повторно называется

векторно-дифференциальной операцией второго порядка.

Конечно, не всякие комбинации имеют смысл, например, комбинация
div (divaG) не имеет смысла, так как diva образует					скалярное поле, от
которого нельзя взять дивергенцию.
Всего осмысленных операций второго порядка пять:
1. div (rotaG),		2. rot (gradU ),		3. div (gradU ),
	4. grad (diva),		5. rot (rota).
Рассмотрим эти комбинации.
G	G G	G		смешанное	произведение трех
1. div (rota )= ( ×a ). Получили

векторов, два из которых равны между собой. В этом случае смешанное

произведение равно нулю, т.е. div (rota )

=0, а это означает, что поле ротора

соленоидалъно.

G

G

)

.

Получили

векторное

произведение двух

2. rot (gradU )= ×

U

G

(

G

коллинеарных векторов и U . Такое векторное произведение равно нулю,

т.е. rot (gradU )= 0G, значит, поле градиента потенциально.

G

G

G G

G

2

+ ∂

2

2

3. div (gradU )= ( U )=

( )U = 2U =

∂ U

U

+ ∂ U .

∂x2

∂y2

∂z2

G

∂2

∂2

∂2

Оператор 2

=

+

+

называется

дифференциальным

∂x

2

∂y2

∂z2

оператором Лапласа

или

лапласианом

и

обозначается

символом

("дельта"), т.е.

G

∂2

∂2

∂2

= 2 =

+

+

.

∂x2

∂y2

∂z2

П.Лаплас (1749-1827) - французский математик, физик и астроном.

72

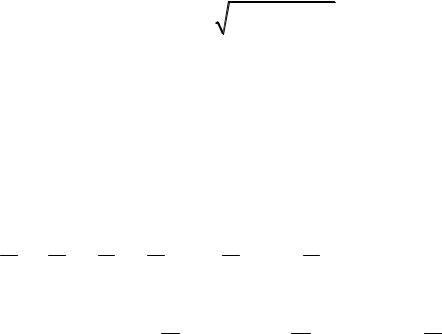
Дифференциальное уравнение		в	частных производных		U = 0
называется уравнением Лапласа. Оно имеет вид
∂2U	+ ∂2U	+	∂2U	= 0 .
∂x2	∂y2		∂z2

Можно рассматривать оператор Лапласа и соответственно уравнение Лапласа на плоскости, т.е.

	=	∂2	+	∂2	и	∂2U	+	∂2U	= 0 .
		∂x2		∂y2		∂x2		∂y2

Функции, удовлетворяющие уравнению Лапласа, называются гармоническими (соответственно в пространстве или на плоскости).

Примерами гармонических функций в пространстве могут служить

функции:	xyz,	1	,	ln		r − z		, где r =	x2 + y2 + z2 .
		r				r + z
На	плоскости						примерами		гармонических	функций	будут:
xy, x2 − y2 , arctg				y	,		ln (x2 + y2 ).
				x

G G	Решение задач				G	G
	G	G	= sin xi +(z	2
Задача 2.15. Найти ( a), если a					+1) j	+ 2 yzk .

Решение. Найдем сначала

G aG=divaG=∂∂xax +∂∂yay +∂∂zaz =∂∂x(sinx)+∂∂y(z2 +1)+∂∂z(2yz)=cosx+0+2y=cosx+2y.

Теперь найдем

G(cosx+2y)=grad(cosx+2y)=∂∂x(cosx+2y)iG+∂∂y(cosx+2y)Gj +∂∂z (cosx+2y)kG= = −sin xiG+ 2 Gj +0k = −sin xiG+ 2 Gj.

Задача 2.16. Найти U , если U = 3x2 yz − y3 z + 4 y2 − 4z2 .

Решение. U = ∂2U + ∂2U + ∂2U .

∂x2 ∂y2 ∂z2

Найдем сначала частные производные первого порядка.

∂∂Ux = 6xyz; ∂∂Uy = 3x2 z −3y2 z +8 y; ∂∂Uz = 3x2 y − y3 −8z.

∂2U	= 6 yz;	∂2U	= −6 yz +8;	∂2U	= −8.
∂x2		∂y2		∂z2

Следовательно, U = 6 yz −6 yz +8 −8 = 0.

73