КОНСПЕКТ ЛЕКЦИЙ 1 часть

Тема 4: ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ

ПЛОСКИХ СЕЧЕНИЙ

Вопросы

4.1Статический момент площади.

4.2Моменты инерции.

4.3Моменты сопротивления.

4.4Определение моментов инерции сечения в случае параллельного переноса осей.

4.5Определение момента инерции при повороте осей.

4.6Главные оси и главные моменты инерции.

4.7Пример и методика расчета геометрических характеристик сложных сечений.

		4.1 Статический момент площади
	y					Статический		момент
						площади относительно оси – это
	xi		dF
						алгебраическая		сумма
ymax
			F			произведений	элементарных
	ρi
		yi				площадок на их расстояние до
					x
	C		ρmax			этой оси.
			xmax			Sx = ∫ yi dF ,	см3, м3 (+;-;0)
						F
	Рис. 4.1 - Геометрические					S y = ∫ xi dF ,	см3, м3 (+;-;0)
						F
	характеристики сечения
						Статический		момент

сложного сечения (состоящего из нескольких простых сечений) относительно некоторой оси равен сумме статических моментов всех частей этого сечения

41

относительно той же оси.

Из теоретической механики известно:

Sx=Fyc; Sy=Fxc,

где xc, yc - координаты центра тяжести сечения.

Тогда координаты центра тяжести сечения можно найти по формулам:

	yc=Sx/F		(4.1)
	хc=Sу/F	.	(4.2)
Оси, проходящие через центр тяжести, называются центральными осями.
Статический момент относительно любой центральной оси равен нулю.

4.2 Моменты инерции.

Различают три вида моментов инерции:

-осевой;

-полярный;

-центробежный.

Осевым моментом инерции относительно некоторой оси называется взятая по всей площади сечения сумма произведений элементарных площадок на квадрат их расстояния до этой оси.

I x	= ∫ yi2dF ,	см4, м4	Ix>0;
	F
I y	= ∫ xi2dF ,	см4, м4	Iy>0.
	F

Полярным моментом инерции относительно некоторой точки (полюса) называется взятая по всей площади сечения сумма произведений элементарных площадок на квадрат расстояния до полюса.

I P = ∫ ρi2 dF ,	см4, м4	IP>0.
F

42

Полярный момент сопротивления Wp - отношение полярного момента инерции к расстоянию до наиболее удаленной точки сечения от полюса.

Wp=Ip/ρmax [м3, см3] Wp>0.

43

где ρі – расстояние от і-той элементарной площадки до полюса.

Сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения этих осей.

IP=Ix+Iy.

Центробежным моментом инерции относительно двух взаимно перпендикулярных осей называется взятая по всей площади сечения сумма произведений элементарных площадок на их расстояния до этих осей.

I xy = ∫ xi yi dF	см4, м4 (+;-;0).
F

Центробежный момент инерции сечения относительно одной или двух осей симметрии равен нулю.

4.3 Моменты сопротивления

Различают моменты сопротивления: осевые и полярный.

Осевым моментом сопротивления Wx, Wy называется отношение соответствующего осевого момента инерции к расстоянию до наиболее удаленной точки сечения от оси.

Wx=Ix/ymax	[м3, см3]	Wx>0;
Wy=Iy/xmax	[м3, см3]	Wy>0.

4.4 Определение моментов инерции сечения

при параллельном переносе осей

Предположим, что моменты инерции Ix, Iy, Ixy данного сечения относительно центральных осей X, Y известны. Возьмем новую систему координат X1, Y1, оси которой параллельны прежним (рис. 4.2).

y1 y

x1

b x

dF

y

y1 x

O

a

x1

O1

Рис. 4.2 - Моменты инерции при параллельном переносе осей

На рисунке 4.2 :	а, b - расстояние между осями
	x1=x+b;	y1=y+a.

Выразим осевой момент инерции относительно осей X1 Y1

I x1 = ∫ y12 dF = ∫ (y + a)2 dF = ∫ y 2 dF + ∫ 2 ya dF + ∫ a 2 dF =Ix+2aSx+a2F.

F F F F F

Если оси x, y – центральные, то Sx=0 и Sy=0. Тогда осевые моменты инерции относительно осей X1 Y1 определим по формулам:

I x =Ix+a2F		(4.3)
1
I y =Iy+b2F	.	(4.4)
1

44

Осевой момент инерции относительно новой оси, параллельной старой центральной оси равен моменту инерции относительно старой оси плюс произведение площади сечения на квадрат расстояния между ними.

Выразим центробежный момент инерции относительно осей X1 Y1

I x y		= ∫ x1 y dF =	∫ (x + b)(y + a)	dF = ∫ xydF + ∫ axdF + ∫ bydF +			∫ abdF =
1	1	1	F	F	F	F	F
		F

=Ixy+aSy+bSx+abF.

Если оси x, y – центральные, то Sx=0 и Sy=0. Тогда центробежный момент инерции относительно осей X1 Y1 определим по формуле:

I x y = Ixy+abF		.	(4.5)
1	1

Центробежный момент инерции относительно новых осей

параллельных старым, проходящих через центр тяжести, равен центробежному моменту инерции относительно старых осей плюс произведение площади сечения на расстояния между осями (a, b).

Данные формулы справедливы только при переходе от центральных осей.

4.5 Определение момента инерции при повороте осей

Определим моменты инерции относительно новых осей X1, Y1, повернутых относительно старых осей на положительный угол α (рис. 4.3).

Правило знаков: угол α считается положительным, если поворот осей происходит против хода часовой стрелки.

45

	y
	y1		A	dF
					x1
	y	M	C
					α +
			α
y1				K	x
	O	B
		x
		x1

Рис. 4.3 - Моменты инерции при повороте осей: х,у - координаты элементарной площади dF

Определим моменты инерции относительно новых осей Х1 и Y1,повернутых относительно старых осей на положительный угол α.

I x1 = ∫ y12 dF

F

y1=AC=AK-KC=AB cosα - OB sinα = y cosα - x sinα; x1=OM+MC=OB cosα – BK sin α = x cosα - y sinα;

I x =	∫	y	2 dF =	∫ (y × cosα - x × sinα )2 dF =
1	F		1	F

= cos2 α ∫ y2dF − 2 sinα cosα ∫ xy dF + sin2 α ∫ x2dF =cos2α Ix+sin2α Iy-Ixysin2α.

F F F

	I x = Ix cos2α + Iy sin2α - Ixysin2α		(4.6)
1
	I y1 = Ix sin2α + Iy cos2α + Ixysin2α		(4.7)
			(4.8)
	Ix1+Iy1=Ix+Iy=const

46

Сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной независимо от угла поворота α.

Выразим центробежный момент инерции относительно осей X1 Y1

I x1 y1	= ∫ x1y1 dF =				1	(Ix-Iy)sin2α+Ixycos2α,
	F			2
I x1 y1		=	1	(Ix-Iy)sin2α+Ixycos2α			.	(4.9)
		2

4.6 Главные оси и главные моменты инерции

Как следует из формул (4.6), (4.7), величины осевых моментов инерции изменяются с изменением угла α. При некотором угле α0, один момент инерции принимает максимальное значение, а второй - минимальное.

Данные моменты инерции являются главными моментами инерции Imax

Imin, а оси - называются главными осями инерции.

Если главные оси проходят через центр тяжести сечения, то они называются главными центральными осями инерции и соответственно моменты инерции - называются главными центральными моментами инерции.

Для определения положения главных осей инерции необходимо взять первую производную от Ix1 относительно α и приравнять ее к нулю. Получим

	tg2α0= –	2I xy			.	(4.10)
		I x	− I y

Величину главных моментов инерции находим по формуле:

		1	[ I x + I y ±		]	.
	I max =			(I x − I y )2 + 4I xy2			(4.11)
		2
	min

47

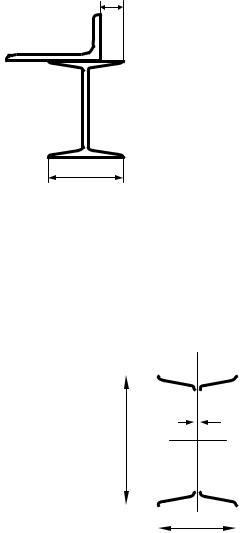
4.7 Пример и методика расчета геометрических характеристик

сложных сечений

Для сложного сечения, состоящего из прокатных профилей, используя таблицы сортамента, определить:

1)положение главных центральных осей;

2)величину моментов инерции относительно главных центральных осей. Также определить при помощи графических построений момент

сопротивления сечения относительно одной главной оси (рис. 4.4). Дано: двутавр №24; уголок 180 х 110 х 12 мм; a = 0,4 b.

a

b

Решение:

1)Выпишем из таблиц сортамента геометрические данные прокатных профилей:

Двутавр №24:

h = 24 см;								y
b = 11,5	см;								s
s = 0,56	см;
			h						x
F = 34,8	см2;
IX = 3460 cм4;
	4						b
IY = 198 см		;

IXY = 0 (т.к. оси X и Y двутавра являются его осями симметрии).

48

Уголок 180х110х12:		d	y
В	= 18 см;
b	= 11 см;	umin
d	= 1,2 см;		vmax
x0	= 2,52 см;	B	x
y0	= 5,97 см;	y0	α0
	= 33,69 см2;
F			d
IX	= 1122,56 cм4;	x0
IY	= 324,09 см4;		b
IU min = 194,28 cм4;
tg α = 0,374 (α = 20° 30' = 20,5° ).
Значение центробежного момента инерции уголка найдем из формулы
для определения положения главных осей инерции сечения:

tg 2α = −	2I XY	.
	I X − IY

(Можно заметить, что данная формула аналогична формуле для определения положения главных площадок при плоском напряженном состоянии.)

Тогда центробежный момент инерции уголка равен:

I XY	= −	tg 2α (I X − IY )	= −	tg41°(1122,56 − 324,09)	= − 347,11см4 .
	2		2

Значение получилось отрицательным, т.к. в сортаменте ось минимум уголка (Umin) проходит через 2 – 4 квадрант. В заданном же сечении уголок развернут так, что его ось минимум пройдет через 1 – 3 квадранты, поэтому в данной задаче значение центробежного момента инерции уголка будем считать положительным.

49

2)Построим заданное сечение в масштабе по размерам, взятым из таблиц сортамента, причем a = 0,4·bдвутавра = 0,4·11,5 = 4,6 см.

3)Выберем начало отсчета.

Удобно за начало отсчета принять центр тяжести двутавра, т.к. в заданном сечении двутавр расположен вертикально (так же, как в сортаменте). Тогда оси двутавра образуют вспомогательную систему координат.

4)Во вспомогательной системе координаты центра тяжести двутавра получатся равными нулю:

xI

= 0;

y I = 0 .

C

C

Из чертежа найдем координаты центра тяжести уголка во

вспомогательной системе:

b двутавра

11,5

xII

= − y

+ a −

= − 5,97 + 4,6

−

= − 4,82 см;

C

0

2

2

y II

h

24

= + x

+

= + 2,52

+

= +14,52 см.

C

0

2

2

5)Определим координаты центра тяжести всего сечения:

	=		x I	F I + x II	F II
xC			C	C		;
				F I + F II
	=		y I	F I + y II	F II
yC			C	C			.
				F I + F II

6)Определим координаты центра тяжести всего сечения:

	=		x I	F I + x II	F II
xC			C	C		;
				F I + F II
	=		y I	F I + y II	F II
yC			C	C			.
				F I + F II

гдеF - площадь всего сечения, [см2];

50