§5. Площадь многоугольника. Теорема существования

Пусть М- множество всех многоугольников на евклидовой плоскости.

Опр. 1.Говорят, что установлено измерение площадей многоугольников, если определено отображение S: М®R₊, такое, что

S1 если F@F^/, то S (F)=S (F^/).

S2 если F=F₁+F₂, то S (F)=S (F₁)+S (F₂) – аддитивность .

S3 S(Р₀)=1, где Р₀-квадрат, построенный на единичном отрезке как на стороне. Положительное число S(F) называется мерой или площадью многоугольника А, а квадрат Р₀- единичным квадратом.

ЗАМЕЧАНИЕРаз речь идет об евклидовой плоскости, с введенной на ней системой координат, то ясно, что единичный отрезок уже выбран.

Теорема существования.На евклидовой плоскости существует хотя бы одно отображение S: M®R₊, удовлетворяющее аксиомам измерениям площадей.

Доказательство. Зададим это отображение явно:

S (F) = (1),

ясно, что это отображение М®R₊ по Ch3. Осталось проверить выполнение аксиом S1-S3.

S1) Пусть F=F^/.$движение, переводящее F в F^/. По теореме о реперах это движение g может быть задано парой соответствующих ортонормированных реперов R и R^/, g(R)=R^/,g(R)=R^/, если M_R(x,y), то g(M)_R^/(x,y). Если A_i(x_i,y_i),I=1,…,n вершины многогранника F в R, то в репере R^/точки А^/_i = g(A_i) будут иметь те же координаты (x_i,y_i), тогда из формулы (1), §4Þ½[]½=½[]½ÞS (F)=S(F^/).

S2) Пусть теперь F=F₁+F₂. По Ch4, F ориентируем так, чтобы>0. На F₁ и F₂ введем ориентацию согласованyeс, это можно сделать, т.к. простой многоугольник гомеоморфен сфере с дыркой, а она ориентируема. Получаем(почему это можно сделать?)

Докажем, что (2).

Пусть М₀…М_К– ломанная, которая разбивает многоугольник F на F₁и F₂.-радиус векторы ее вершин. Вершины многоугольника обозначим так, чтобы А₁-М₀-Аn и А_S–М_К-А_S+1,радиус - векторы точек А_i. Тогда

A_s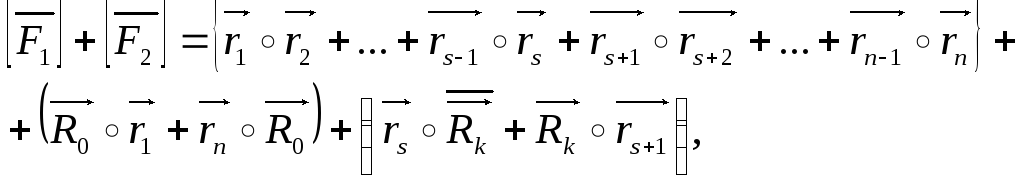

ноЕсли же М₀совпадает с А₁, тои первая скобка равна

,(если R_kсовпадает сисовпадает с, то сразу). Значит, оба отрицательными быть не могут, т.к.>0. Пусть>0, если<0, то из (1) получаем<, что противоречит Ch 2.S(F)=S(F₁)+S(F₂).

S3) Пусть Р₀квадрат. Рассмотрим единичный квадрат ОА₁А₂А₃в системе координатО(0,0), А₁(1,0), А₂(1,1), А₃(0,1).

=2S(P₀)=1

Теорема доказана.

§6. Теорема единственности

Предварительно докажем две теоремы о площади известных фигур, (не то, что установили, а произвольные)

Th1Если S: М®R₊ - отображение, удовлетворяющее аксиомам измерения площадей и Р – это прямоугольник со сторонами х и у, то S (Р)=ху.

Доказательство: Пусть S- отображение удовлетворяющее S1-S3. Если Р₁=Р₂, то S(Р₁)=S(Р₂) , а два прямоугольника равны, если у них равны соответствующие стороны х и у, значитSфункция от двух переменных со значениями в R₊. Обозначим ее¦(х, у)=S(Р).

Функция ¦(х, у) обладает следующими свойствами:

¦(х, у)=¦(у,х) это следует из §1, т.к. тогда два прямоугольника равны

¦(х₁+х₂,у)=¦(х₁,у)+¦(х₂,у)

¦(х,у)=¦(1,у)*х.

у у

х₁х₂

Докажем 3). Зафиксируем y₀, тогда f(x,y₀)=g(x) из (2) следует, что"x_1,x₂ >0. g(x₁+x₂)=g(x₁)+g(x₂),значит g– это линейная функция на R₊, а значит, имеет вид g(х)=кх, т.е. f(х, у)=к (у) х. И, т.к.Þпри х=1 f(1,у)=к (у), тоÞ(3) доказано.

f(1,у)=f (у, 1)=f (1,1) у, но f (1,1)=1Þf(1,у)=у (3)Þf (х,у)=ху.

Th2 Если S:М®R₊-отображение удовлетворяющее аксиомам измерения площадей, а Т-треугольник у которого х- одна из его сторон, а у- соответствующая высота, то S(Т)=ху.Доказательство самостоятельно (идея:)

Th(единственность площади) Если выбран едининичный отрезок, то существует не более одного отображения S: М®R₊, удовлетворяющего аксиомам измерения площадей.

Доказательство.Пусть S^/:М®R₊удовлетворяет S1-S3. Пусть F-произвольный многоугольник. Разобьем его на конечное число треугольников F=D₁+…+D_n.Тогда по S2: S(R)=;S^/(F)=, то S(D_i)=S^/(D_i)ÞS(F)=S^/(F), значит отображения S и S^/совпадают ч.т.д.

Следствие1. При любом способе разложения многоугольника F на конечное множество треугольников сумма площадей этих треугольников одна и та же.

Доказательство очевидно из аксиомыS2 и Тhединственности.

Следствие 2. Если вершины многоугольника А₁А₂…А_nв прямоугольной системе координат имеют координаты А_i(x_i,y_i) , i=1,2,…,n, то