Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Тюменский государственный нефтегазовый университет”

Институт нефти и газа

Методические указания и задания к практическим

занятиям по “Теории автоматического управления”

на тему “ Метод припасовывания граничных условий” для студентов специальностей АТП и УИТС очной и заочной форм обучения

Тюмень 2004

Утверждено редакционно-издательским отделом Тюменского государственного нефтегазового университета

Составители: к.т.н., доцент Макарова Л.Н., к.т.н. Макаров А.В.,

аспирант Фомин В.В.

Ответственный редактор: к.т.н., доцент Макарова Л.Н.

@ Государственное образовательное учреждение высшего

профессионального образования “Тюменский государственный

нефтегазовый университет”

Тюмень 2004

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

“Тюменский государственный нефтегазовый университет”

Институт нефти и газа

Методические указания и задания к практическим

занятиям по “Теории автоматического управления”

на тему “ Метод припасовывания граничных условий” для студентов специальностей АТП и УИТС очной и заочной форм обучения

Председатель РИС Проректор

Перевощиков С.И. “ ” 200 г.

Рассмотрено на заседании

Подписи авторов Ученого совета ИНиГ

Протокол № от 200 г.

Подпись

Председатель совета

Рассмотрено на заседании

методической комиссии

Протокол № от 200 г

Подпись

Председатель метод. комиссии

Тюмень 2004

1. Основные определения

Метод “припасовывания” граничных условий представляет собой точный метод расчета в кусочно-линейных системах. Для каждого из линейных интервалов записывают решение уравнения с неизвестными произвольными постоянными, которые находят последовательно. Для этого значения координат и их производных в конце предыдущего и начале последующего интервала приравнивают. Это возможно в том случае, если координаты и их производные не совершают скачков.

2. Примеры построения фазовой траектории методом “припасовывания” граничных условий

2.1. Исследовать переходный процесс в системе со структурной схемой, приведенной на (Рис.1). Значения характеристик равны: к=2с; b=0,5; с=5.

х₂

-b

b

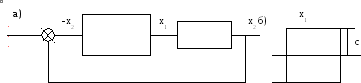
Error: Reference source not found

Рис.1. Структурная схема исследуемой системы

Решение. Дифференциальное уравнение замкнутой системы имеет вид:

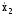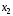+kF()=0

+C , для х₂>+b;

–b<x₂<b при x₁>0

F(x₂)=

–C , для x₂<-b;

–b<x₂<b при x₁>0

Запишем дифференциальное уравнение для каждого из линейных интервалов:

Для F(x₂)=с +kc=0 (1)

Для F(x₂)= –c 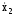+kc=10 (2)

Решение для (1)

dx₂/dt= –10 => dx₂= –10dt

x₂= –10t+c₁; (3)

для (2) x₂=10t+c₂ (4)

Для (3) начальные условия имеют вид х₂(0) , тогда с₁₁=х₂(0), т.е. с учетом начальных условий решение (3) имеет вид:

х₂(t)= –10t+x₂(0)

Найдём момент перехода к решению (4).

Это происходит, когда x₂(t)= –b, т.е.

b= –10t+x₂(0) => t₁=(x₂(0)+b)/10,

при этом x₂=10t+c₂ ( из (4)) равно –b, из этого условия находим с₂₁.

c₂= –(2b+x₂(0)), т.е.

решение во второй области, начиная от момента времени t₁, имеет вид

x₂(t)=10t–(2b–x₂(0)).

Следующий момент перехода к решению (3) наступит, когда x₂(t)=b;

–b=10t–(2b–x₂(0))

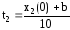; находим с₁₂:

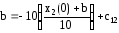
с₁₂=2b+x₂(0)

x₂(t)= –10t+(2b+x₂(0)),

Находим следующий момент времени, соответствующий х₂(t)= –b и соответствующую постоянную времени и т.д.

2.2. Методом “припасовывания” граничных условий провести исследование переходных процессов на фазовой плоскости для нелинейной системы, приведенной на (Рис.2)

Error: Reference source not found

Рис.2. Структурная схема нелинейной системы к примеру 2.2

Нелинейный элемент представляет собой чувствительный элемент со статической характеристикой в виде релейной характеристики с зоной нечувствительности (Рис.1б).

Исполнительное устройство имеет передаточную функцию вида

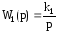(5)

Передаточная функция объекта регулирования равна

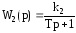(6)

Заметим, что k=k₁k₂

Тогда линейная часть системы будет описываться уравнением

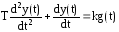(7)

Уравнение нелинейного элемента

g(t)=F[ε(t)], (8)

Запишем уравнение сравнивающего элемента

ε(t)=x(t) – y(t). (9)

Предположим, что задающее воздействие x(t)=0. Тогда уравнение нелинейной САУ будет иметь следующий вид

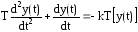(10)

Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них составляется линейное дифференциальное уравнение:

Ι уч. 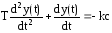, еслиy > b, (11)

ΙΙ уч. , если |y| ≤ b, (11)

ΙΙΙ уч. 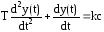, еслиy < –b, (11)

Для фазовой плоскости введем обычные координаты y и z =dy/dt.

Исключим в уравнениях (11) время

;

;

;

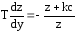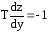Разделяя переменные и интегрируя, получим уравнения фазовых траекторий для участков 1-3 нелинейной характеристики:

Ι уч. 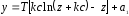, (12)

ΙΙ уч. , (12)

ΙΙΙ уч. 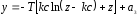, (12)

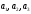–произвольные постоянные интегрирования , определяемые начальными условиями.

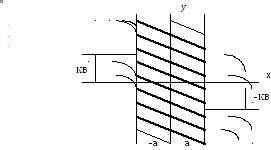
Сначала на фазовой плоскости наносят линии переключения, разделяющие плоскость на три области. Это линии перехода от одного участка нелинейной характеристики к другой.

Error: Reference source not found

Рис.3. Фазовые траектории

Затем по уравнению (12) строят фазовые траектории. При этом должны учитываться общие правила построения фазовых траекторий.

Построение фазовых траекторий в пакете “MATHCAD 2000”

В программе MATHCAD 2000 процесс построения фазовых траекторий производится следующим образом:

Зададим значения коэффициентов

Зададим начальные значения для вектора y:

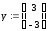
Определим функцию D по трем линейным участкам нелинейной статической характеристики, задающую производную, приведя дифференциальное уравнение второго порядка к системе двух дифференциальных уравнений первого порядка:

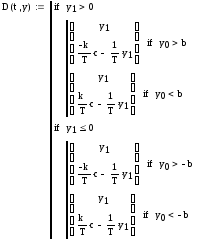
Найдем матрицу решения:

Построим траекторию на фазовой плоскости, предполагая, что первый столбец матрицы решения содержит точки, в которых ищется решение дифференциального уравнения, второй— содержит значения найденного решения, то есть y(t) и, наконец, третий столбецсодержит первые производные этого решения, то есть dy(t)/dt.

b

–b

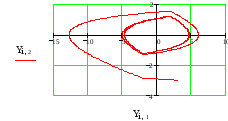
Рис.4. Фазовая траектория

На графике линии переключения — штриховые линии. Задавая различные начальные условия можно получить все возможные фазовые траектории исследуемой нелинейной системы.