
- •Пусть дано уравнение
- •Графический метод отделения корней
- •Из графика видно, что .
- •Метод половинного деления
- •Число ξ, которое является общим пределом последовательностей {an} и {bn}, это точный корень уравнения (1). Оценим погрешность решения на n-м шаге:
- •Предельное значение является единственным корнем уравнения на отрезке при .
-
Рис.1.
-
Из графика видно, что .
-
Метод половинного деления
Пусть уравнение (1) имеет на отрезке [a,b] один корень, а функция f(x) на данном отрезке непрерывна и f(a)·f(b)<0. Разделим отрезок [a,b] пополам точкой x1=(а+b)/2. Если f(x1)≠0 , то для продолжения вычислений выберем ту часть промежутка, где знаки функции различны. Концы полученного отрезка обозначим [a1,b1] и снова разделим отрезок [a1,b1] пополам точкой x2=(а+b)/2 и т. д. В результате получим последовательность вложенных отрезков [a1,b1], [a2,b2],… [an,bn],…таких, что
f(an)·f(bn)<0, bn - an=2 -n·(b-a), (n=1,2,…).
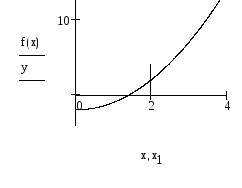
Рис.2. К объяснению метода половинного деления
-
Число ξ, которое является общим пределом последовательностей {an} и {bn}, это точный корень уравнения (1). Оценим погрешность решения на n-м шаге:
ξ-an ≤ an-bn .
Считаем до тех пор, пока длина промежутка не станет меньше заданной точности ε . В качестве ответа возьмем середину отрезка [an,bn].
Пример3. Найти, используя пакет MATHCAD, методом половинного деления корень уравнения x4-x3-2x2+3x-3=0 на промежутке [1,2]
Функция koren(a,b,ε) возвращает длину отрезка, который будет меньше заданной точности ε и значение корня на этом промежутке, если на концах отрезка [a,b] функция имеет противоположные знаки, или сообщение об отсутствии корня, в противном случае.

Метод хорд
В этом методе нелинейная функция f(x) на отделенном промежутке
(a,b) заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
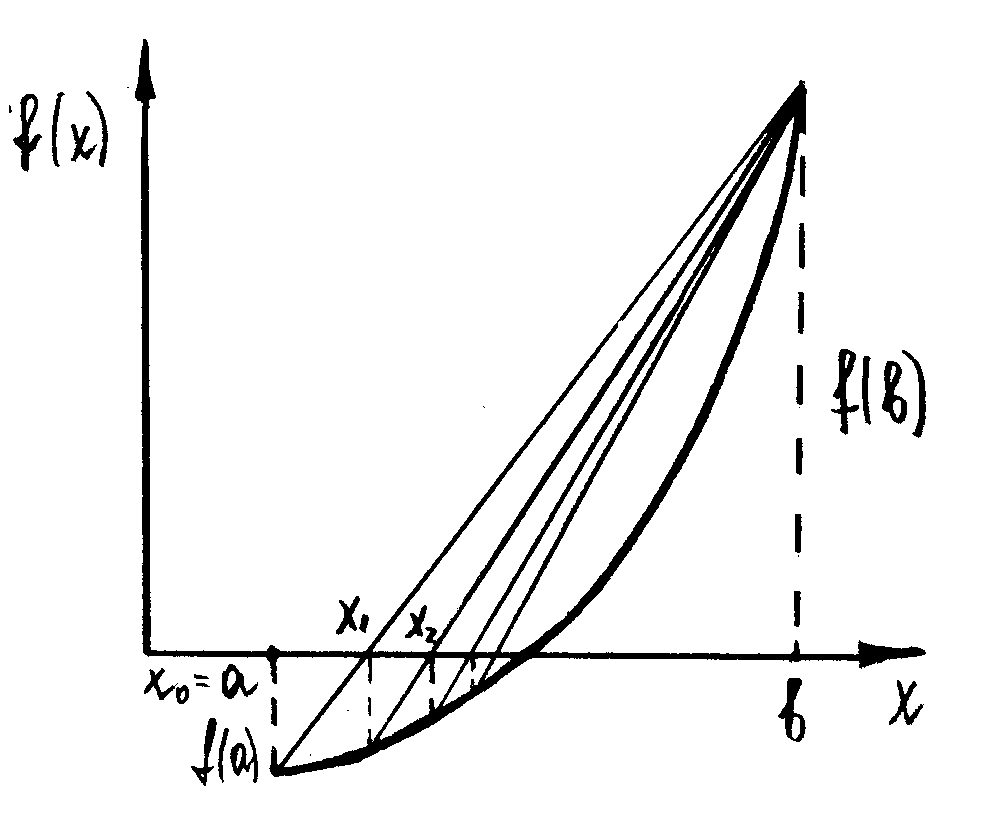
Рис.3. Метод хорд. Неподвижен правый конец промежутка b
Уравнение
хорды:
![]() .
Найдем точку пересечения хорды с
горизонтальной осью. Полагая
.
Найдем точку пересечения хорды с
горизонтальной осью. Полагая
![]() и
и
![]() ,
получим
,
получим
![]()
Точку
x1
принимаем за новую границу отрезка, где
содержится корень. Через эту точку с
координатами (x1,f(x1))
и соответствующую
границу предыдущего интервала (b,f(b))
опять проводят хорду, находят
![]() и т.д., получая последовательность
x1,x2,x3,…xn,…,
сходящуюся к корню уравнения.
и т.д., получая последовательность
x1,x2,x3,…xn,…,
сходящуюся к корню уравнения.
Вторая
производная
![]() сохраняет
постоянный знак на
сохраняет
постоянный знак на
![]() .
Следовательно, возможны два случая.
Если f(b)·f
"(b)>0,
то хорда имеет правый фиксированный
конец, причем последовательность
x0,x1,…xn
приближается
к корню слева.
За начальное приближение x0,
естественно, берут a
.
Следовательно, возможны два случая.
Если f(b)·f
"(b)>0,
то хорда имеет правый фиксированный
конец, причем последовательность
x0,x1,…xn
приближается
к корню слева.
За начальное приближение x0,
естественно, берут a
![]() ;
;
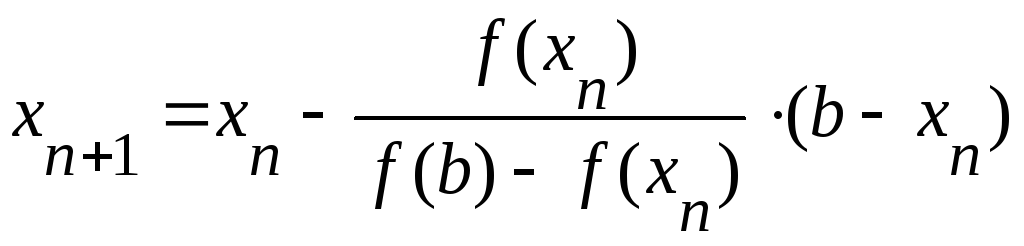 ;
;
![]() ;
;
![]() .
.
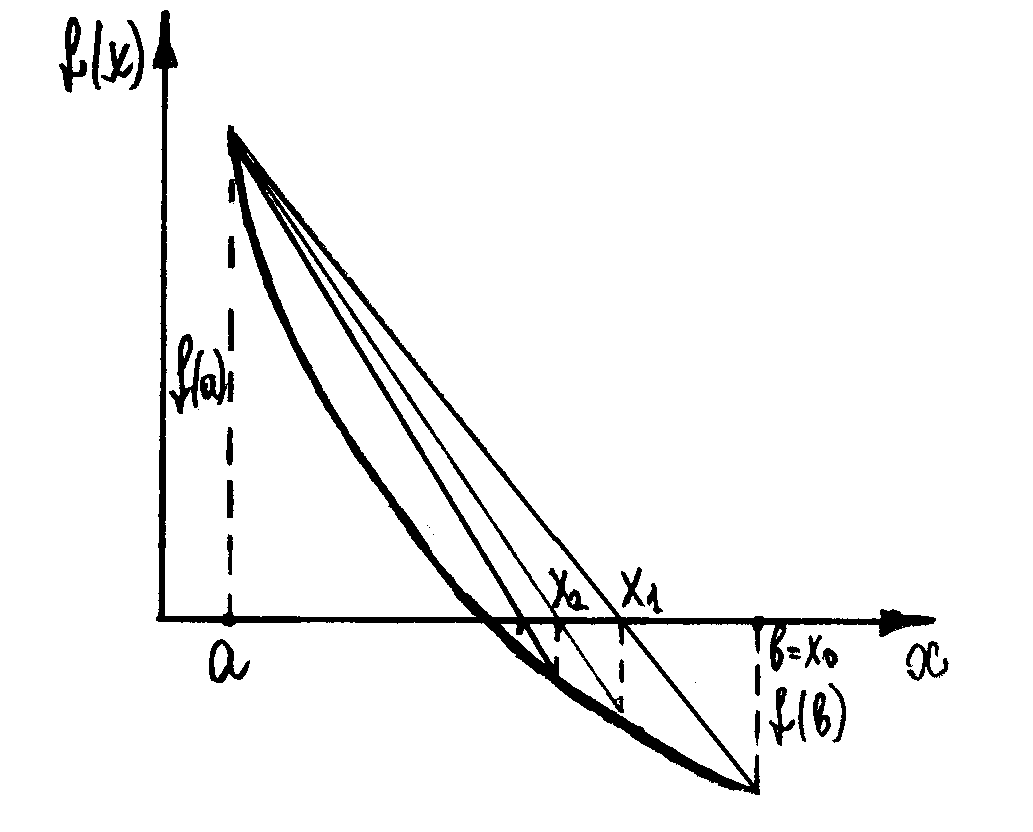
Рис. 4. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x0,x1,…xn … приближается к корню справа. За начальное приближение x0, берут b
![]() ;
;
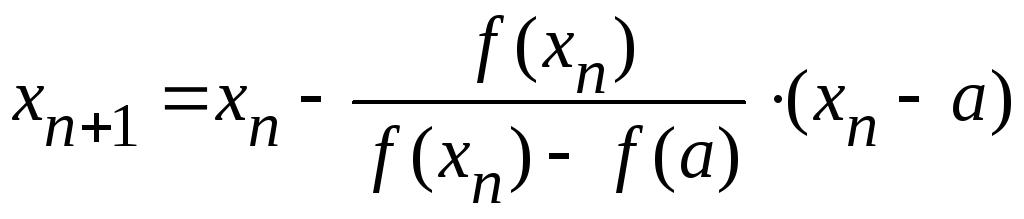 ;
;
![]() ;
;
![]() .
.
Для оценки точности можно воспользоваться формулой
![]() ,
,
где
![]() -точный
корень,
-точный
корень,
![]() - приближенный корень,
- приближенный корень,
![]() ,
,
![]() на промежутке [a,b].
Считаем до тех пор пока, не выполнится
условие
на промежутке [a,b].
Считаем до тех пор пока, не выполнится
условие
![]() .
Если имеет место неравенство
.
Если имеет место неравенство
![]() ,
то счет можно прекратить, когда.
,
то счет можно прекратить, когда.
![]()
Пример 4 Найти методом хорд корень уравнения x4-x-1=0
Решение находим, используя пакет MATHCAD


Метод Ньютона – метод касательных
Пусть
![]() -
корень уравнения
-
корень уравнения
![]() отделен на отрезке
отделен на отрезке
![]() ,
причем
,
причем
![]() и
и
![]() непрерывны и сохраняют определенные
знаки на этом же отрезке
непрерывны и сохраняют определенные
знаки на этом же отрезке
![]() .
Найдя какое-нибудь n-е
значение корня
.
Найдя какое-нибудь n-е
значение корня
![]() (
(![]() ),
уточним его по методу Ньютона. Для этого
положим
),
уточним его по методу Ньютона. Для этого
положим
![]() ,
где
,
где
![]() -
считаем малой величиной. Разложим
функцию f(x)
в ряд Тейлора в окрестности точки x
n
по степеням
h
n
Тогда можно
записать:
-
считаем малой величиной. Разложим
функцию f(x)
в ряд Тейлора в окрестности точки x
n
по степеням
h
n
Тогда можно
записать:
![]()
Ограничимся
двумя членами ряда и так как![]() ,
то:
,
то:
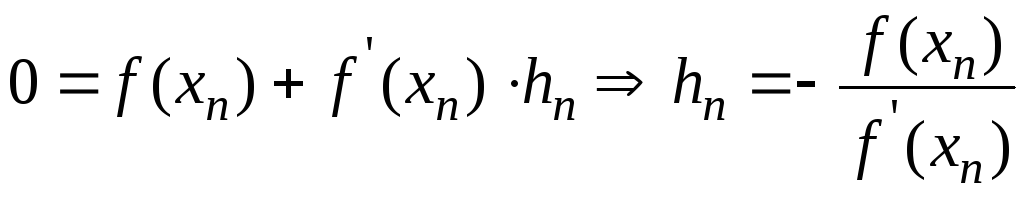 .
.
Учитывая
найденную поправку hn:,получим
![]() (n=0,1,2,…).
(n=0,1,2,…).
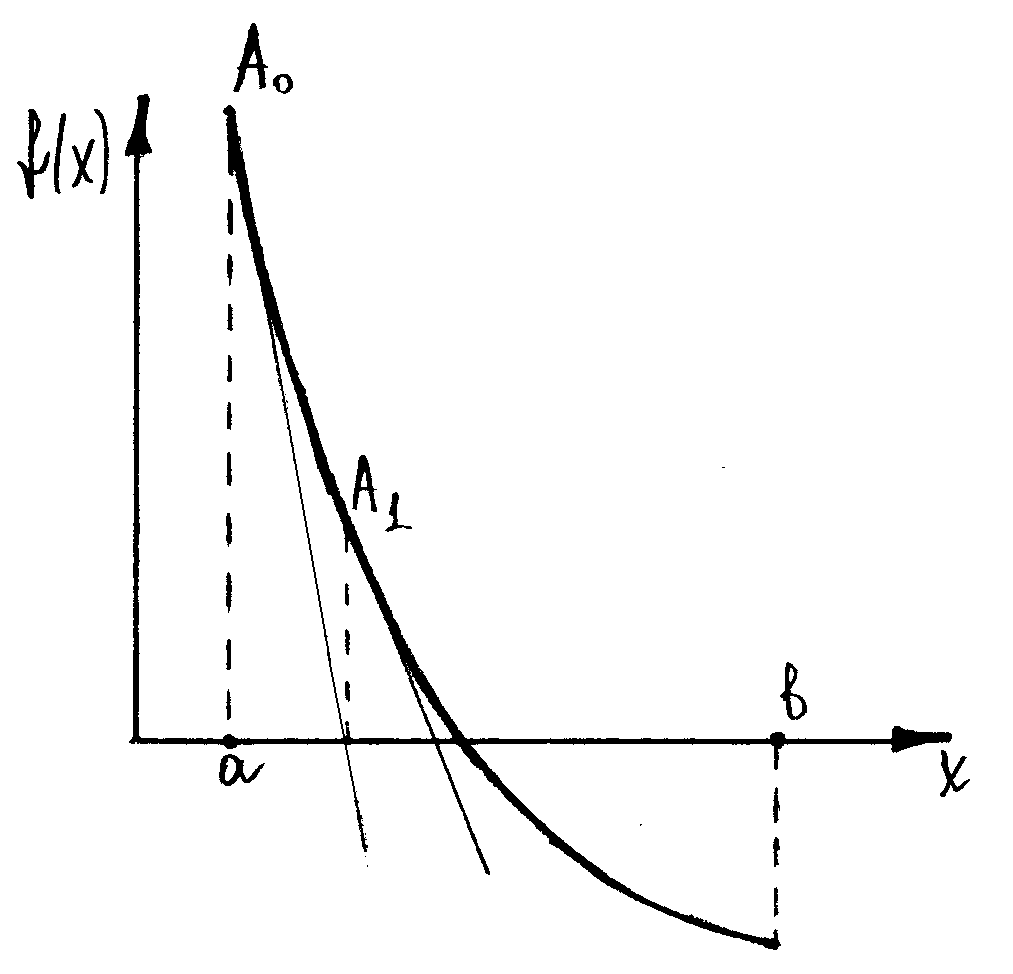
Рис.5. Метод касательных. Начальное приближение x0=a
По-другому
этот метод называется методом касательных.
Если в точке
![]() провести касательную к функции f(x)
, то ее
пересечение с осью ОХ и будет новым
приближением x1
корня
уравнения
провести касательную к функции f(x)
, то ее
пересечение с осью ОХ и будет новым
приближением x1
корня
уравнения
Хорошим
начальным приближением
![]() является то значение, для которого
выполнено неравенство
является то значение, для которого
выполнено неравенство
![]() .
.
Погрешность
вычислений:
![]() ,
или
,
или
![]()
Теорема
2:
Если
![]() ,
причем
,
причем
![]() и
и
![]() отличны
от нуля и сохраняют определенные знаки
при
отличны
от нуля и сохраняют определенные знаки
при
![]() ,
то, исходя из начального приближения
,
то, исходя из начального приближения![]() ,
удовлетворяющего условию
,
удовлетворяющего условию
![]() ,
можно вычислить методом Ньютона
единственный корень
,
можно вычислить методом Ньютона
единственный корень
![]() уравнения
уравнения
![]() с любой степенью точности.
с любой степенью точности.
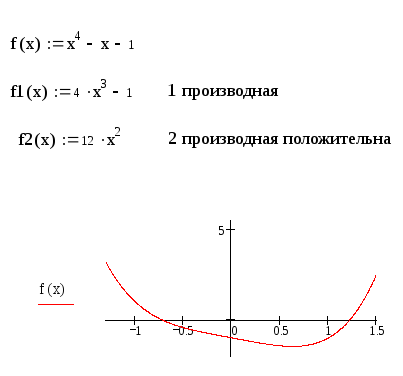
Пример 5 Найти методом Ньютона корень уравнения x4-x-1=0, предварительно отделив корни графически

Модифицированный метод Ньютона
Если
производная
![]() мало изменяется на отрезке [a,b]
то в формуле
мало изменяется на отрезке [a,b]
то в формуле
![]() можно положить
можно положить
![]() .
Отсюда для корня
.
Отсюда для корня
![]() уравнения
уравнения
![]() получаем последовательные приближения
по формуле
получаем последовательные приближения
по формуле
 Рис.6
Модифицированный метод Ньютона
Рис.6
Модифицированный метод Ньютона
![]() (n=0,1,…)..
(n=0,1,…)..
Метод секущих
Заменим производную функции f(x) в точке xn на функцию F(x) в этой же точке. Подставим ее вместо производной в формулу Ньютона
![]() ,
,
![]() .
.
В методе секущих требуются задать для начала счета два значения x0 и x1. Отрезок [x0, x1] не обязательно должен содержать корень уравнения.
Метод итерации
Пусть дано уравнение
![]() ,
(1)
,
(1)
где
![]() -
непрерывная функция. Заменим его
равносильным уравнением
-
непрерывная функция. Заменим его
равносильным уравнением
![]() .
(2)
.
(2)
Выберем
каким-либо способом приближенное
значение корня
![]() и подставим его в правую часть уравнения
(2). Получим некоторое число
и подставим его в правую часть уравнения
(2). Получим некоторое число
![]() .
Повторим данную процедуру с x1,
получим
.
Повторим данную процедуру с x1,
получим
![]() .
Повторяя описанную процедуру, будем
иметь последовательность чисел:
.
Повторяя описанную процедуру, будем
иметь последовательность чисел:
![]() ,
где n=1,2,….
(3)
,
где n=1,2,….
(3)
Пусть
у этой последовательности существует
предел
![]() .
Перейдем к пределу в равенстве (3).
Предполагая функцию φ(х)
непрерывной,
найдем:
.
Перейдем к пределу в равенстве (3).
Предполагая функцию φ(х)
непрерывной,
найдем:
![]() или
или
![]() .
.
Таким
образом, предел является корнем уравнения
![]() и может быть вычислен по формуле (3) с
любой степенью точности.
и может быть вычислен по формуле (3) с
любой степенью точности.
На рисунке дана геометрическая интерпретация метода итераций в зависимости от знака производной функции φ(х).
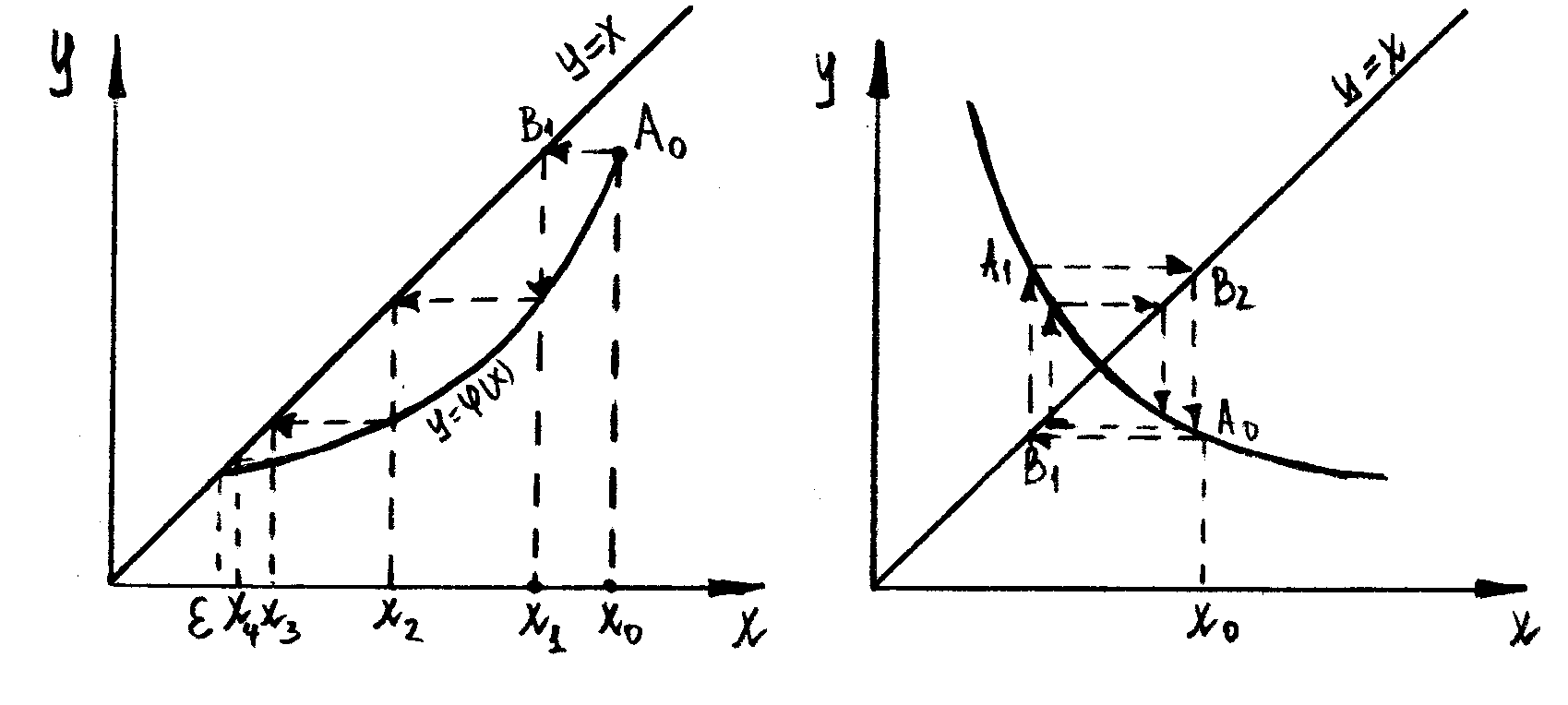
Рис.7. φ’(х)>0 Рис.8. φ’(х)<0..
Достаточное условие сходимости процесса итераций определяется в следующей теореме.
Теорема
3: Пусть
функция
![]() определена и дифференцируема на отрезке
определена и дифференцируема на отрезке
![]() ,
причем все ее значения
,
причем все ее значения
![]() .
Тогда, если существует правильная дробь
q
такая, что
.
Тогда, если существует правильная дробь
q
такая, что![]()
![]() при
при
![]() ,
то
,
то
