
- •Лекція № 3
- •2. Лінійна рекурентна послідовність, що генерується рзлзз
- •3. Запис станів двійкового регістру через супроводжуючу матрицю
- •4. Вираз елементів рекуренти через початковий стан
- •5. Анулюючі та мінімальні многочлени послідовностей
- •6. Існування тричленних похідних співвідношень
- •7. Знаходження покриваючого співвідношення для лінійної рекуренти методом Гаусса
- •7. Алгоритм Берлекемпа-Мессі
- •8. Теорема про лінійну складність комбінуючого генератора
3. Запис станів двійкового регістру через супроводжуючу матрицю
Розглянемо
матрицю
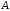 ,
для якої елементи останнього стовпця
,
для якої елементи останнього стовпця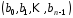 з номерами
з номерами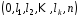 дорівнюють одиниці, а решта – нулі.
дорівнюють одиниці, а решта – нулі.
 ,
,
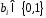 ,
,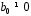 .
.
Матриця
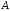 називається супроводжуючою матрицею
послідовності.
називається супроводжуючою матрицею
послідовності.
Матриця
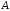 оборотна і
оборотна і
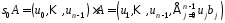 ,
,
тобто
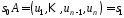 .
.
Звідки
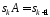 і
і
 ,
,
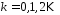 .
.
Зокрема, якщо
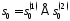 ,
,
то
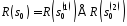 ,
,
де рекуренти додаються поелементно.
Приклад.
Супроводжуюча
матриця для розгортки
РЗЛЗЗ з рекурентним співвідношенням
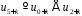 має
вид:
має
вид:
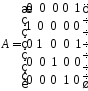
Точки
знімання мають номери 0 і 2, тому в
останньому стовпці елементи
 і
і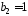 ,
а решта – нулі.
,
а решта – нулі.
Виразимо послідовність початкових станів 11000 10001 00011 00110 … через супроводжуючу матрицю:
 ;
;
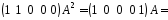
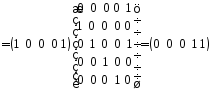 ;
;
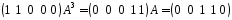 ;
;
……………………………………………………….
Стан
регістру після
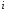 -го
такту роботи дорівнює
-го
такту роботи дорівнює
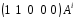 .
.
Матричний
запис дозволяє записати одночасно
послідовність станів для декількох
початкових станів, тому що, наприклад,
операції
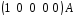 і
і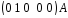 можна записати як добуток матриць
можна записати як добуток матриць
 .
.
Це дозволяє розглядати рекуренту з векторним початковим станом.
4. Вираз елементів рекуренти через початковий стан
Співвідношення
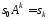 дозволяє легко обчислити стан
дозволяє легко обчислити стан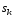 при дуже великих
при дуже великих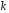 ,
оскільки існують ефективні методи
обчислення степеня матриці.
,
оскільки існують ефективні методи
обчислення степеня матриці.
Виявляється,
що так само неважко визначити номери
бітів з початкового стану
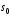 ,
комбінація яких дає біт
,
комбінація яких дає біт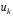 рекурентної послідовності
рекурентної послідовності з номером
з номером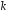 .
.
Нехай
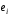 ,
,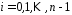 ,
– рядки одиничної матриці
,
– рядки одиничної матриці порядку
порядку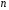 .
Розглянемо кожний рядок як початковий
стан відповідної рекуренти
.
Розглянемо кожний рядок як початковий
стан відповідної рекуренти .
.
Запишемо
рекуренти
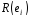 як рядки деякої матриці
як рядки деякої матриці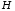 і розглянемо її як послідовність
векторів-стовпців
і розглянемо її як послідовність
векторів-стовпців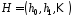 .
Послідовність
.
Послідовність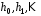 підпорядковується тому ж самому
рекурентному співвідношенню, що і
підпорядковується тому ж самому
рекурентному співвідношенню, що і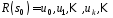 .
Початковий стан
.
Початковий стан становлять
становлять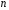 векторів
векторів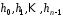 ,
що за побудовою є стовпцями матриці
,
що за побудовою є стовпцями матриці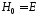 .
.
Координати
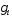 наступного вектора
наступного вектора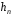 можна отримати як останні біти станів
можна отримати як останні біти станів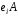 ,
або одною матричною операцією: вибратиостанній
стовпець
з матриці
,
або одною матричною операцією: вибратиостанній
стовпець
з матриці
 .
Таким чином,
.
Таким чином,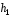 – першій, а
– першій, а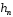 – останній стовпець матриці
– останній стовпець матриці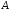 .
Наступний стовпець
.
Наступний стовпець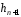 буде останнім стовпцем в матриці
буде останнім стовпцем в матриці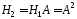 ,
першим стовпцем якої є
,
першим стовпцем якої є ,
і так далі,
,
і так далі,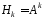 .
.
У добутку
матриць
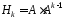 останній стовпець матриці
останній стовпець матриці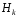 дорівнює добутку матриці
дорівнює добутку матриці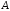 на останній стовпець матриці
на останній стовпець матриці .
Це означає, що сусідні стовпці матриці
.
Це означає, що сусідні стовпці матриці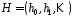 пов’язані співвідношенням
пов’язані співвідношенням
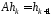 ,
,
або
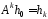 ,
,
де
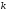 – довільне ціле число, оскільки матриця
– довільне ціле число, оскільки матриця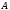 оборотна. Таким чином, ми легко можемо
обчислити вектори
оборотна. Таким чином, ми легко можемо
обчислити вектори .
Назвемо стовпці матриці
.
Назвемо стовпці матриці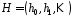 характеристичними
векторами.
характеристичними
векторами.
Нехай
 .
Оскільки
.
Оскільки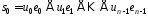 ,
то
,
то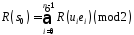 ,
тобто
,
тобто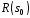 є сумою рядків матриці
є сумою рядків матриці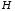 з коефіцієнтами
з коефіцієнтами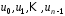 .
В термінах стовпців
.
В термінах стовпців це означає, що біт рекуренти з номером
це означає, що біт рекуренти з номером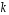 можна записати як
можна записати як ,
де
,
де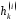 – координати вектора
– координати вектора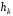 .
Номери цих координат, відмінні від нуля,
вказують, сумою яких компонент початкового
стану
.
Номери цих координат, відмінні від нуля,
вказують, сумою яких компонент початкового
стану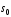 є біт
є біт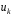 .
.
Приклад.
Розглянемо
одночасно послідовності станів регістра
з
рекурентним співвідношенням
 для
для
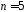 початкових
станів.
початкових
станів.
Нехай
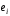 ,
, ,
– рядки одиничної матриці
,
– рядки одиничної матриці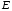 порядку
порядку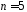 .
Розглянемо кожний рядок як початковий
стан відповідної рекуренти
.
Розглянемо кожний рядок як початковий
стан відповідної рекуренти .
.
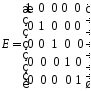
Перший
крок (перехід від початкового стану
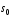 до стану з номером
до стану з номером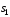 )
дає
)
дає
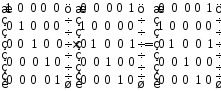
тобто
 .
.
Другий
крок (перехід від стану
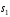 до стану
до стану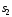 )
дає
)
дає

тобто
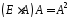 і так далі.
і так далі.
Тепер
треба сумістити стани, щоб отримати
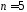 рекурентних послідовностей, які підписані
одна під одною
рекурентних послідовностей, які підписані
одна під одною
Маємо
5 початкових станів (рядки матриці
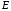 ),
далі 5 станів після кроку 1 (рядки матриці
),
далі 5 станів після кроку 1 (рядки матриці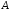 )
і 5 станів після кроку 2 (рядки матриці
)
і 5 станів після кроку 2 (рядки матриці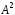 ).
).

Суміщаємо стани з перших рядків: 1000010, з других рядків: 0100001 і так далі. Але це теж саме, що суміщати сусідні матриці, бо останні 4 стовпчики попередньої матриці і перші 4 стовпчики наступної матриці співпадають, тобто маємо:
 .
.
Розгорнемо
матрицю
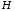 до кінця періоду. У цієї матриці стовпці
з номерами 0-4 утворюють матрицю
до кінця періоду. У цієї матриці стовпці
з номерами 0-4 утворюють матрицю ,
стовпці з номерами 1-5 утворюють матрицю
,
стовпці з номерами 1-5 утворюють матрицю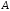 ,
стовпці з номерами 2-6 утворюють матрицю
,
стовпці з номерами 2-6 утворюють матрицю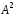 і т.д. Таким чином, матриці, що перетинаються
по 4-х стовпцях мають вид
і т.д. Таким чином, матриці, що перетинаються
по 4-х стовпцях мають вид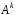 ,
, і їхні останні стовпці розташовані
поруч. Але за правилами множення матриць
з рівності
і їхні останні стовпці розташовані
поруч. Але за правилами множення матриць
з рівності випливає, що останній стовпець матриці
випливає, що останній стовпець матриці дорівнює добутку матриці
дорівнює добутку матриці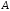 на останній стовпець матриці
на останній стовпець матриці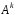 ,
тобто
,
тобто ,
,
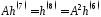 ,і
так далі.
,і
так далі.
Оскільки
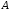 – обротна, то цей закон виконується для
довільних цілих
– обротна, то цей закон виконується для
довільних цілих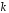 ,
зокрема,
,
зокрема, ,
, .
Таким чином, ми можемо швидко обчислити
.
Таким чином, ми можемо швидко обчислити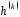 не розгортаючи рекуренту
не розгортаючи рекуренту
Згадаємо, що поелементна сума рекурент, які задовольняють одне й теж саме рекурентне співвідношення, є рекурентою, що також задовольняє це співвідношення з початковим станом, що дорівнює сумі початкових станів рекурент-доданків.
Нехай
 – довільний початковий стан, який для
нашого прикладу матиме вид
– довільний початковий стан, який для
нашого прикладу матиме вид .
.
Розглянемо
добуток
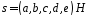 ,
який дорівнює лінійній комбінації
рядків матриці
,
який дорівнює лінійній комбінації
рядків матриці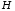 з коефіцієнтами
з коефіцієнтами .
За попереднім, послідовність
.
За попереднім, послідовність – рекурента, початковий стан якої є
– рекурента, початковий стан якої є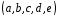 ,
а біт з номером
,
а біт з номером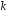 є добутком
є добутком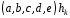 .
Оскільки ми легко можемо побудувати
.
Оскільки ми легко можемо побудувати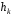 ,
то ми знаємо номери ненульових координат
цього вектора, а це дає нам змогу вказати
номери елементів початкового стану,
сума яких дорівнює біту з номером
,
то ми знаємо номери ненульових координат
цього вектора, а це дає нам змогу вказати
номери елементів початкового стану,
сума яких дорівнює біту з номером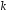 ,
не знаючи ні початкового стану, ні
значення біту з номером
,
не знаючи ні початкового стану, ні
значення біту з номером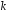 .
.
