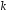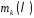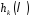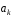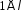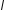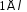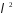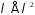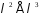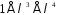- •Лекція № 3
- •2. Лінійна рекурентна послідовність, що генерується рзлзз
- •3. Запис станів двійкового регістру через супроводжуючу матрицю
- •4. Вираз елементів рекуренти через початковий стан
- •5. Анулюючі та мінімальні многочлени послідовностей
- •6. Існування тричленних похідних співвідношень
- •7. Знаходження покриваючого співвідношення для лінійної рекуренти методом Гаусса
- •7. Алгоритм Берлекемпа-Мессі
- •8. Теорема про лінійну складність комбінуючого генератора
7. Алгоритм Берлекемпа-Мессі
Алгоритм
Берлекемпа-Мессі призначений для
знаходження конфігурації регістра
зсуву з лінійним зворотним зв’язком
мінімальної довжини, який генерує задану
скінчену послідовність, що складається
з елементів поля
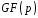 .
Розглянемо випадок поля
.
Розглянемо випадок поля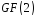 .
.
Конфігурація
регістра – це довжина регістра
 та перелік коефіцієнтів лінійної форми
та перелік коефіцієнтів лінійної форми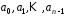 ,
яка реалізує функцію зворотного зв’язку.
,
яка реалізує функцію зворотного зв’язку.
Нехай
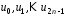 – скінченна послідовність над
полем
– скінченна послідовність над
полем
 ,
,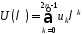 – покриваючий многочлен. Для
– покриваючий многочлен. Для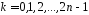 визначимо многочлени
визначимо многочлени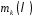 ,
,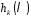 ,
цілі числа
,
цілі числа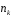 і елементи
і елементи
 наступним чином:
наступним чином:
Для
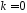 покладаємо:
покладаємо:
 ,
,
 ,
,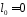 .
.
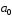 – коефіцієнт
при степені
– коефіцієнт
при степені
 в многочлені
в многочлені ,
,
Для
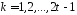
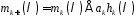 ,
,
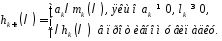
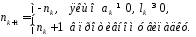
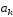 – коефіцієнт
при степені
– коефіцієнт
при степені
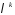 в многочлені
в многочлені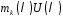 .
.
Шуканий мінімальний многочлен визначається рівністю
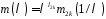 .
.
Якщо
відомо, що степінь
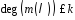 ,
то покладемо
,
то покладемо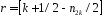 .
Тодімінімальний
многочлен визначається рівністю
.
Тодімінімальний
многочлен визначається рівністю
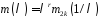 .
.
Приклад.
Знайти конфігурацію
РЗЛЗЗ мінімальної довжини, який генерує
скінченну послідовність над полем
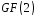 :1100011011.
:1100011011.
Розв’язання. Запишемо покриваючий многочлен для згенерованої частини послідовності:
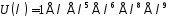 .
.
Для
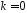 покладаємо:
покладаємо:
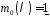 ,
,
 ,
,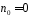 ,
,
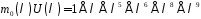 ,
,
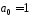 – коефіцієнт
при степені
– коефіцієнт
при степені
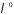 в многочлені
в многочлені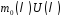 .
.
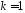
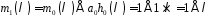 ,
,
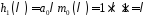 ,
оскільки
,
оскільки
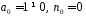 .
.
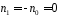 ,
оскільки
,
оскільки
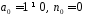 .
.
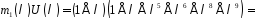
 ,
,
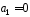 –коефіцієнт
при степені
–коефіцієнт
при степені
 в многочлені
в многочлені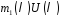 .
.
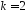
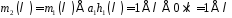 ,
,
 ,
оскільки
,
оскільки
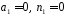 .
.
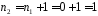 ,
оскільки
,
оскільки
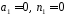 .
.
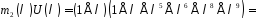
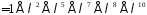 ,
,
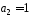 –коефіцієнт
при степені
–коефіцієнт
при степені
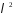 в многочлені
в многочлені .
.
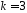
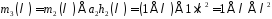 ,
,
 ,
,
оскільки
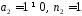 .
.
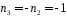 ,
оскільки
,
оскільки
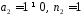 .
.
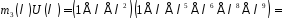
 ,
,
 – коефіцієнт
при степені
– коефіцієнт
при степені
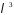 в многочлені
в многочлені .
.
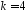
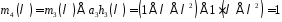 ,
,
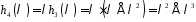 ,
,
оскільки
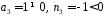 .
.
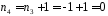 ,
оскільки
,
оскільки
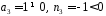 .
.
 ,
,
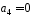 – коефіцієнт
при степені
– коефіцієнт
при степені
 в многочлені
в многочлені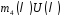 .
.
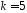
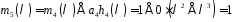 ,
,
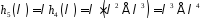 ,
оскільки
,
оскільки
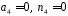 .
.
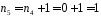 ,
оскільки
,
оскільки
 .
.
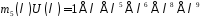 ,
,
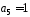 – коефіцієнт
при степені
– коефіцієнт
при степені
 в многочлені
в многочлені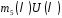 .
.

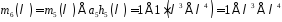 ,
,
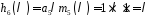 ,
оскільки
,
оскільки
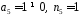 .
.
 ,
оскільки
,
оскільки
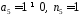 .
.
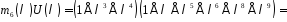
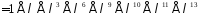 .
.
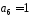 – коефіцієнт
при степені
– коефіцієнт
при степені
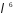 в многочлені
в многочлені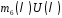 .
.
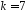
 ,
,
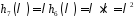 ,
оскільки
,
оскільки
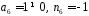 .
.
 ,
оскільки
,
оскільки
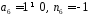 .
.
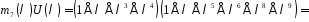
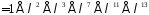 ,
,
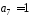 – коефіцієнт
при степені
– коефіцієнт
при степені
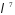 в многочлені
в многочлені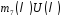 .
.
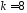
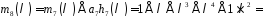
 ,
,
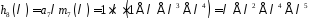 ,
,
оскільки
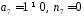 .
.
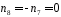 ,
оскільки
,
оскільки
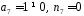 .
.
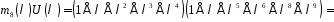
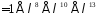 ,
,
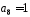 –коефіцієнт
при степені
–коефіцієнт
при степені
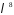 в многочлені
в многочлені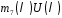 .
.

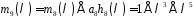 ,
,
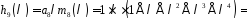
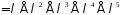 ,
оскільки
,
оскільки
 .
.
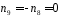 ,
оскільки
,
оскільки
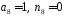 .
.
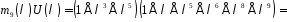
 ,
,
 – коефіцієнт
при степені
– коефіцієнт
при степені
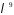 в многочлені
в многочлені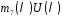

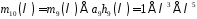 ,
,
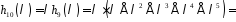
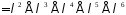 ,
оскільки
,
оскільки
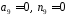 .
.
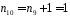 ,
оскільки
,
оскільки
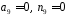 .
.
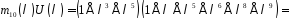
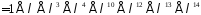 ,
,
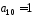 – коефіцієнт
при степені
– коефіцієнт
при степені
 в многочлені
в многочлені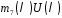 .
.
Протокол роботи алгоритму зручно оформлювати у вигляді таблиці:
|
|
|
|
|
|
|
0 |
1 |
|
0 |
1 |
|
1 |
|
|
0 |
0 |
|
2 |
|
|
1 |
1 |
|
3 |
|
|
–1 |
1 |
|
4 |
1 |
|
0 |
0 |
|
5 |
1 |
|
1 |
1 |
|
6 |
|
|
–1 |
1 |
|
7 |
|
|
0 |
1 |
|
8 |
|
|
0 |
1 |
|
9 |
|
|
0 |
0 |
|
10 |
|
|
1 |
1 |
Оскільки
відомо, що степінь
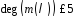 ,
то покладемо
,
то покладемо .
Тодімінімальний
многочлен визначається рівністю
.
Тодімінімальний
многочлен визначається рівністю
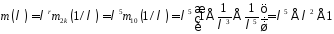 .
.
8. Теорема про лінійну складність комбінуючого генератора
Безпосередньо для генерації гами РЗЛЗЗ не підходять. На практиці застосовуються комбінації залежних РЗЛЗЗ, що взаємно впливають на формування своїх послідовних заповнень.
Нагадаємо
основні способи комбінування двійкових
РЗЛЗЗ за допомогою функції
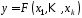 ускладнення від
ускладнення від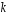 двійкових змінних, що приймає значення
з
двійкових змінних, що приймає значення
з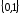 .
Такі функції називаються булевими.
.
Такі функції називаються булевими.
Означення.
Довжина
найменшого РЗЛЗЗ, який для деякого
початкового стану генерує скінченну
або періодичну послідовність
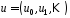 називаєтьсялінійною
складністю послідовності
називаєтьсялінійною
складністю послідовності
 .
.
Можна довести, що для довільної періодичної послідовності можна знайти РЗЛЗЗ, що її генерує.
Очевидно, достатньо велика лінійна складність є необхідною для криптографічно стійких послідовностей.

Рис. 1 Способи комбінування залежних РЗЛЗЗ
Розглянемо
комбінуючий генератор
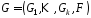 ,
що складається з
,
що складається з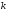 РЗЛЗЗ
РЗЛЗЗ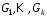 і булевої функції ускладнення
і булевої функції ускладнення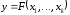 у вигляді загального многочлена:
у вигляді загального многочлена:
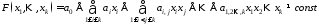 .
.
Зіставимо
булевій функції
 функцію
функцію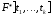 з аргументами з поля дійсних чисел виду
з аргументами з поля дійсних чисел виду
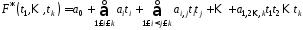 .
.
Сформулюємо окремий випадок теореми про лінійну складність комбінуючого генератора.
Теорема
(про лінійну складність комбінуючого
генератора).
Нехай мінімальні многочлени регістрів
 є примітивними, а всі числа
є примітивними, а всі числа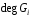 ,
, – попарно взаємно прості. Тоді лінійна
складність послідовності, що генерується
генератором
– попарно взаємно прості. Тоді лінійна
складність послідовності, що генерується
генератором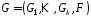 дорівнює
дорівнює .
.