
- •Лекція № 3
- •2. Лінійна рекурентна послідовність, що генерується рзлзз
- •3. Запис станів двійкового регістру через супроводжуючу матрицю
- •4. Вираз елементів рекуренти через початковий стан
- •5. Анулюючі та мінімальні многочлени послідовностей
- •6. Існування тричленних похідних співвідношень
- •7. Знаходження покриваючого співвідношення для лінійної рекуренти методом Гаусса
- •7. Алгоритм Берлекемпа-Мессі
- •8. Теорема про лінійну складність комбінуючого генератора
5. Анулюючі та мінімальні многочлени послідовностей
над
полем

Означення.
Анулюючим
многочленом послідовності
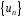 ,
називається такий многочлен
,
називається такий многочлен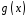 над полем
над полем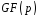 ,
що
,
що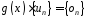 ,
де
,
де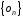 –
нульова послідовність.
–
нульова послідовність.
Означення.
Мінімальним
многочленом
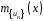 послідовності
послідовності
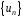 ,
називається нормований анулюючий
многочлен найменшого степеня.
,
називається нормований анулюючий
многочлен найменшого степеня.
Мінімальним
многочленом рекурентної послідовності
над полем
 є многочлен
є многочлен
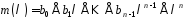 ,
,
який є
мінімальним многочленом матриці
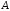 ,
оскільки вона для цього многочлену є
супроводжуючою. За побудовою, для кожного
такту
,
оскільки вона для цього многочлену є
супроводжуючою. За побудовою, для кожного
такту роботи РЗЛЗЗ він задає співвідношення
роботи РЗЛЗЗ він задає співвідношення
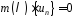 ,
,
або
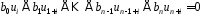 ,
де
,
де
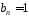 .
.
Початковий
стан рекуренти складається з
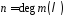 елементів.
елементів.
Приклад.
Мінімальним
многочленом рекурентної послідовності
з рекурентним співвідношенням
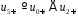 буде многочлен
буде многочлен
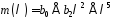
або
 .
.
Покажемо, що для нашої рекуренти існують інші рекурентні співвідношення.
Розглянемо
многочлен виду
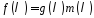 і побудуємо для нього супроводжуючу
матрицю, порядок якої дорівнює
і побудуємо для нього супроводжуючу
матрицю, порядок якої дорівнює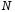 .
Тоді коефіцієнти
.
Тоді коефіцієнти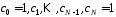 многочлена
многочлена
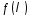 задають для деякої рекуренти співвідношення
виду
задають для деякої рекуренти співвідношення
виду
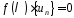
або
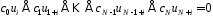 .
.
Коефіцієнти
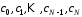 можна легко отримати
за
правилами добутку многочленів
можна легко отримати
за
правилами добутку многочленів
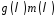 ,
за якими набір коефіцієнтів многочлена
,
за якими набір коефіцієнтів многочлена
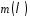 зсувається на величину степеня кожного
одночлену
зсувається на величину степеня кожного
одночлену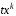 ,
що входить до
,
що входить до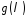 ,
а потім ці зсуви виду
,
а потім ці зсуви виду підсумовуються. Таким чином, вектор
коефіцієнтів
підсумовуються. Таким чином, вектор
коефіцієнтів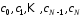 дорівнює сумі деяких таких зсувів.
дорівнює сумі деяких таких зсувів.
Многочлени
виду
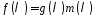 називаються похідними,
або покриваючими многочленами
рекурентної послідовності з мінімальним
многочленом
називаються похідними,
або покриваючими многочленами
рекурентної послідовності з мінімальним
многочленом
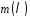 .
.
Застосуємо
до нашої рекуренти
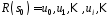 рекурентне співвідношення з коефіцієнтами
рекурентне співвідношення з коефіцієнтами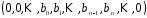 .
Рекурента задовольняє співвідношенню
для довільного
зсуву, а це значить, що вона буде
задовольняти рекурентне співвідношення
з коефіцієнтами
.
Рекурента задовольняє співвідношенню
для довільного
зсуву, а це значить, що вона буде
задовольняти рекурентне співвідношення
з коефіцієнтами
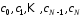 .
.
Нехай
тепер задані дві рекурентні послідовності
з відомими рекурентними співвідношеннями
(мінімальними многочленами
 ,
,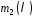 )
і початковими станами
)
і початковими станами і
і ,
розмірності яких задовольняють умову
,
розмірності яких задовольняють умову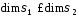 .
.
Рекурентне
співвідношення для суми цих рекурент
задають коефіцієнти многочлена
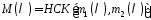 ,
тому що цей многочлен є покриваючим для
кожної з рекурент. Тому довжина
(розмірність) початкового стану
,
тому що цей многочлен є покриваючим для
кожної з рекурент. Тому довжина
(розмірність) початкового стану дорівнює
дорівнює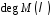 .
.
Якщо ми
продовжимо
 і
і
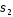 ,
за відповідними рекурентними законами
до
,
за відповідними рекурентними законами
до бітів, то отримаємо послідовності
бітів, то отримаємо послідовності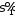 і
і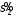 ,
з яких отримаємо
,
з яких отримаємо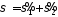 .
.
6. Існування тричленних похідних співвідношень
Як нам
відомо, для того, щоб послідовність
векторів
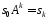 ,
,
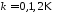 ,
мала максимальний період
,
мала максимальний період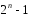 ,
слід вибирати мінімальний многочлен
,
слід вибирати мінімальний многочлен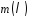 примітивним многочленом степеня
примітивним многочленом степеня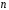 над полем
над полем .
Тому будемо вважати многочлен
.
Тому будемо вважати многочлен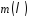 примітивним.
примітивним.
У цьому
випадку послідовність
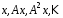 ,
при
,
при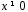 пробігає всі ненульові двійкові вектори,
тобто довільний вектор
пробігає всі ненульові двійкові вектори,
тобто довільний вектор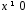 дорівнює вектору
дорівнює вектору при деякому
при деякому .
.
Виберемо
в матриці
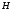 ,
рядками якої є рекуренти
,
рядками якої є рекуренти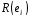 два ненульових нерівних вектори
два ненульових нерівних вектори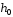 ,
,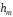 і обчислимо вектор
і обчислимо вектор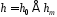 .
За попереднім, існує ціле
.
За попереднім, існує ціле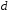 ,
таке, що
,
таке, що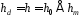 .
.
При цьому
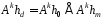 ,
,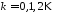 ,
,
звідки
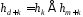 і
і
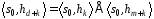 .
.
Таким чином, для нашої рекуренти виконується тричленне співвідношення
 .
.
7. Знаходження покриваючого співвідношення для лінійної рекуренти методом Гаусса
Нехай
довжина рекурентної послідовності
 з
мінімальним многочленом
з
мінімальним многочленом
 дорівнює
або
дорівнює
або
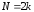 ,
або
,
або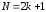 ,
де
,
де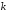 більше довжини регістру
більше довжини регістру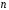 .
Нехай
.
Нехай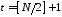 ,
тобто відповідно
,
тобто відповідно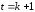 або
або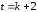 .
Складемо матрицю
.
Складемо матрицю з елементів послідовності
з елементів послідовності з наступними номерами:
з наступними номерами:
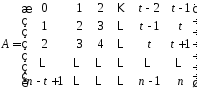 .
.
Двійкова
матриця
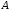 для випадку
для випадку має
має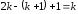 рядків. Аналогічно, для випадку
рядків. Аналогічно, для випадку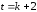 кількість рядків дорівнює
кількість рядків дорівнює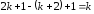 .
Таким чином, шаблон для рекурентного
співвідношення вкладається у кожному
рядку декілька разів.
.
Таким чином, шаблон для рекурентного
співвідношення вкладається у кожному
рядку декілька разів.
Матриця
 має розмірність або
має розмірність або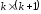 ,
або
,
або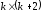 .
Тому її стовпці лінійно залежні. Таким
чином, система рівнянь
.
Тому її стовпці лінійно залежні. Таким
чином, система рівнянь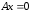 має ненульовий розв’язок
має ненульовий розв’язок і ми доходимо до висновку, що довільний
відрізок довжини
і ми доходимо до висновку, що довільний
відрізок довжини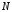 породжується РЗЛЗЗ довжиною не більше
породжується РЗЛЗЗ довжиною не більше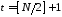 .
.
Розв’язок
системи можна розглядати як шаблон для
деякого перевірочного співвідношення,
яке виконується для послідовності
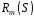 .
Відповідний многочлен є анулюючим
(покриваючим) для
.
Відповідний многочлен є анулюючим
(покриваючим) для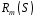 ,
тобто має ділитися на
,
тобто має ділитися на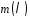 .
.
Приклад.
Для послідовності
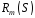 =1100011011101
з
мінімальним многочленом
=1100011011101
з
мінімальним многочленом
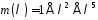 побудувати
покриваючий
многочлен методом Гаусса.
побудувати
покриваючий
многочлен методом Гаусса.
Розв'язання.
Оскільки
довжина
рекурентної
послідовності дорівнює
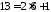 ,
,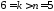 ,
а
,
а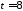 ,
то двійкова матриця
,
то двійкова матриця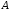 має розмірність
має розмірність .
Складемо матрицю
.
Складемо матрицю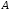 з елементів послідовності
з елементів послідовності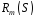 з наступними номерами:
з наступними номерами:
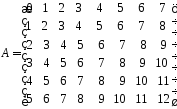
тобто

Знайдемо
ненульовий розв’язок системи рівнянь
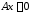 .
Застосуємо метод Гаусса:
.
Застосуємо метод Гаусса:



Невідомі
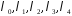 – базисні, невідомі
– базисні, невідомі – вільні. Виразимо базисні невідомі
через вільні:
– вільні. Виразимо базисні невідомі
через вільні:
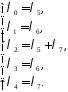
Надамо
вільним невідомим довільних значень,
наприклад,
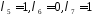 .
Будемо мати
.
Будемо мати .
.
Переконаємося
в тому, що отриманий
 задає
шаблон перевірочного співвідношення
для
задає
шаблон перевірочного співвідношення
для
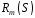 .
Запишемо покриваючий многочлен
.
Запишемо покриваючий многочлен
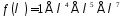 .
.
Перевіримо
результат діленням на мінімальний
многочлен
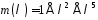 .
Поділимо
.
Поділимо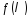 на
на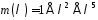 :
:
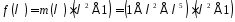 .
.
Зауваження. Для знаходження мінімального многочлена цим методом необхідно перебирати довжину шуканого регістру та після відновлення многочленів перевіряти, чи відповідне рекурентне співвідношення виконується для всього відрізку послідовності. Для швидкого знаходження мінімального многочлена для відрізку довільної рекуренти існує спеціальний алгоритм (Берлекемпа-Мессі).
