
- •Практичне заняття № 1 Тема: Скінченновимірні векторні простори над полем
- •1. Поняття векторного простору над полем
- •2. Лінійна залежність системи векторів Означення. Лінійною комбінацією векторів векторного просторуназивається векторвигляду
- •3. Ранг матриці
- •4. Базис і розмірність векторного простору
- •6. Системи лінійних алгебраїчних рівнянь (загальна теорія)
- •Слар сумісна .
- •Слар має єдиний розв’язок
- •Слар має безліч розв’язків
- •Зміст практичного заняття
4. Базис і розмірність векторного простору
Означення.
Базисом
векторного простору
 називається така впорядкована система
векторів
називається така впорядкована система
векторів ,
що
,
що
1) вона лінійно незалежна;
2)
кожен вектор
 простору
простору лінійно виражається через вектори цієї
системи, тобто
лінійно виражається через вектори цієї
системи, тобто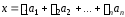 .
.
Означення.
Векторний простір
 називається
називається -вимірним,
якщо в ньому існує базис з
-вимірним,
якщо в ньому існує базис з
 елементів. Число
елементів. Число називаєтьсярозмірністю
простору і позначається
називаєтьсярозмірністю
простору і позначається
 .
Простір скінченної розмірності
називається скінченновимірним.
Простір, в якому можна знайти будь-яке
число лінійно незалежних векторів
називається нескінченновимірним.
.
Простір скінченної розмірності
називається скінченновимірним.
Простір, в якому можна знайти будь-яке
число лінійно незалежних векторів
називається нескінченновимірним.
Отже, розмірність векторного простору – це максимальне число лінійно незалежних векторів цього простору.
Теорема
(про зв'язок між базисом і розмірністю).
Система векторів
 утворює в просторі
утворює в просторі розмірності
розмірності базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору
базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору .
.
5.
Координати вектора у векторному просторі.
Розкладання вектора за базисом. Для
того, щоб вектори з векторного простору
 можна було б задавати за допомогою чисел
і зводити операції над векторами до
операцій над числами, вводиться поняття
координат вектора.
можна було б задавати за допомогою чисел
і зводити операції над векторами до
операцій над числами, вводиться поняття
координат вектора.
Нехай
 – деякий базис векторного простору
– деякий базис векторного простору .
Тоді будь-який вектор
.
Тоді будь-який вектор
 можна подати у вигляді (1):
можна подати у вигляді (1): ,
де
,
де – деякі дійсні числа, причому єдиним
чином. В цьому випадку вираз (1) називається
розкладом вектора
– деякі дійсні числа, причому єдиним
чином. В цьому випадку вираз (1) називається
розкладом вектора за базисом
за базисом .
.
Означення.
Коефіцієнти розкладу (1)
називаються координатами
вектора в даному базисі. Упорядкований
набір координат вектора називається
його координатним рядком і позначається
 :
:

 .
.
Таким
чином, базис дає змогу кожен вектор
однозначно зобразити рядком чисел –
координат цього вектора. Це зображення
дозволяє виконувати над векторами
лінійні операції за правилами лінійних
операцій над матрицями-рядками: якщо
 і
і в деякому базисі, то
в деякому базисі, то
 ,
,
 .
.
Разом
із координатними рядками можна розглядати
координатні стовпці
 ,
отримані транспонуванням
,
отримані транспонуванням -матриці
-матриці .
.
6. Системи лінійних алгебраїчних рівнянь (загальна теорія)
Нехай задана система лінійних алгебраїчних рівнянь
 (3)
(3)
з матрицею

і розширеною матрицею
 .
.
Систему (3) можна записати у вигляді
 (4)
(4)
Згадаємо,
що розв’язком
системи лінійних алгебраїчних рівнянь
(3) називається впорядкований набір з
 чисел
чисел такий, що після заміни невідомих
такий, що після заміни невідомих числами
числами кожне з рівнянь системи (3) перетворюється
на тотожність. Система, що має хоча б
один розв’язок, називаєтьсясумісною,
а якщо система не має жодного розв’язку,
вона називається несумісною.
Дві системи з одними ф тими самими
невідомими, які мають одну й ту саму
множину розв’язків, називаються
рівносильними
(еквівалентними).
кожне з рівнянь системи (3) перетворюється
на тотожність. Система, що має хоча б
один розв’язок, називаєтьсясумісною,
а якщо система не має жодного розв’язку,
вона називається несумісною.
Дві системи з одними ф тими самими
невідомими, які мають одну й ту саму
множину розв’язків, називаються
рівносильними
(еквівалентними).
Теорема
Кронекера-Капеллі.
Система
лінійних алгебраїчних рівнянь (3)
сумісна тоді і тільки тоді, коли ранг
матриці
 системи дорівнює рангу розширеної
матриці
системи дорівнює рангу розширеної
матриці системи.
системи.
Слар сумісна .
Якщо
для заданої системи виконується рівність
 ,
то цю систему називають системою рангу
,
то цю систему називають системою рангу .
.
Нехай
система (3) сумісна і її ранг дорівнює
 .
.
Означення.
Базисними рівняннями
називаються рівняння системи, яким
відповідають
 базисних рядків матриці
базисних рядків матриці системи.Базисною
підсистемою називається
підсистема всіх базисних рівнянь
системи.
системи.Базисною
підсистемою називається
підсистема всіх базисних рівнянь
системи.
Теорема (про сумісну систему). Сумісна система лінійних алгебраїчних рівнянь еквівалентна будь-якій своїй базисній підсистемі.
Нехай
для системи (3) базисну підсистему
утворюють перші
 рівнянь,
тобто базисною є підсистема
рівнянь,
тобто базисною є підсистема
 (5)
(5)
Очевидно,
що ранг системи не перебільшує числа
невідомих, тобто завжди виконується
нерівність
 .
Звідси випливає
.
Звідси випливає
Теорема (про число розв’язків системи) 1. Якщо ранг сумісної системи дорівнює числу невідомих, то система має єдиний розв’язок.
