
- •Лекція 1 Тема: Скінченновимірні векторні простори
- •1. Поняття, приклади і найпростіші властивості векторного простору над полем
- •3. Ранг матриці
- •4. Базис і розмірність векторного простору
- •5. Координати вектора у векторному просторі. Розкладання вектора за базисом
- •2) Розкладемо вектор за базисом:
- •Розв’язуючи цю систему будь-яким способом, знайдемо , ,.
- •6. Ізоморфізм векторних просторів
- •7. Системи лінійних алгебраїчних рівнянь (загальна теорія)
- •Слар сумісна .
- •Слар має єдиний розв’язок
- •Слар має безліч розв’язків
- •8. Підпростори векторного простору
Ю.Д.Жданова. Лекції з ВГПМ. М1 Прикладні аспекти ЛА. Лекція № 1
Лекція 1 Тема: Скінченновимірні векторні простори
План лекції:
Поняття, приклади і властивості векторного простору над полем
Лінійна залежність системи векторів.
Ранг матриці.
Базис і розмірність векторного простору.
Координати вектора у векторному просторі. Розкладання вектора за базисом.
Ізоморфізм векторних просторів.
Системи лінійних алгебраїчних рівнянь (загальна теорія).
Підпростори векторного простору.
1. Поняття, приклади і найпростіші властивості векторного простору над полем
У різних розділах математики лінійні операції додавання і множення на число виконуються не тільки над векторами, а й над різними іншими об’єктами: матрицями, функціями, многочленами, тощо. Можливість підходити до цих об’єктів із загальної точки зору дає поняття векторного (лінійного) простору.
Нехай
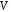 – непорожня множина елементів будь-якої
природи, які будемо позначати
– непорожня множина елементів будь-якої
природи, які будемо позначати і нехай
і нехай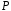 – деяке довільне числове поле, елементи
якого будемо позначати
– деяке довільне числове поле, елементи
якого будемо позначати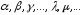 .
Визначимо в множині
.
Визначимо в множині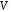 операцію додавання елементів:
операцію додавання елементів: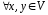
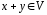 і операцію множення елемента на число
з поля
і операцію множення елемента на число
з поля
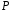 :
:
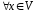
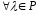
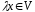 .
.
Означення.
Множина
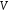 називаєтьсявекторним
(лінійним)
простором,
якщо в
називаєтьсявекторним
(лінійним)
простором,
якщо в
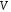 визначені алгебраїчна операція додавання
і операція множення на числа з поля
визначені алгебраїчна операція додавання
і операція множення на числа з поля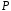 ,
причому виконані наступні умови (аксіоми
векторного простору):
,
причому виконані наступні умови (аксіоми
векторного простору):
1.
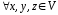
 – асоціативність додавання;
– асоціативність додавання;
2.
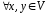
 – комутативність додавання ;
– комутативність додавання ;
3.
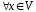
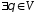 :
: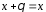 – існування нульового елемента ;
– існування нульового елемента ;
4.
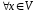
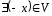 :
: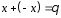 – існування протилежного елемента;
– існування протилежного елемента;
5.
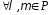
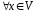
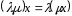 – асоціативність множення на число;
– асоціативність множення на число;
6.

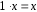 .
.
7.
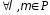

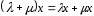 – дистрибутивність відносно додавання
чисел ;
– дистрибутивність відносно додавання
чисел ;
8.

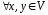
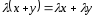 – дистрибутивність відносно додавання
елементів;
– дистрибутивність відносно додавання
елементів;
Елементи
векторного простору називаються
векторами,
елемент
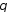 називається
нульовим вектором (нуль-вектором).
називається
нульовим вектором (нуль-вектором).
Будемо
позначати векторний простір, визначений
на множині
 через
через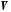 або
або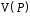 .
Якщо поле
.
Якщо поле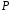 є поле дійсних чисел
є поле дійсних чисел ,
то векторний простір
,
то векторний простір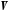 називаєтьсядійсним
векторним простором; якщо
поле
називаєтьсядійсним
векторним простором; якщо
поле
 є полем комплексних чисел
є полем комплексних чисел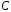 ,
то векторний простір
,
то векторний простір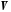 називаєтьсякомплексним
векторним простором.
називаєтьсякомплексним
векторним простором.
Приклади векторних просторів:
1)
Множина
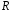 дійсних чисел із звичайними операціями
додавання і множення є дійсним векторним
простором. Множина
дійсних чисел із звичайними операціями
додавання і множення є дійсним векторним
простором. Множина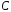 комплексних чисел відносно операцій
додавання комплексних чисел і множення
комплексних чисел на дійсні числа є
дійсний векторний простір
комплексних чисел відносно операцій
додавання комплексних чисел і множення
комплексних чисел на дійсні числа є
дійсний векторний простір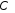 .
.
2)
Множина
всіх геометричних векторів звичайного
тривимірного простору з початком в
точці
 відносно операцій додавання векторів
і множення векторів на число утворює
дійсний векторний простір
відносно операцій додавання векторів
і множення векторів на число утворює
дійсний векторний простір .
.
Множина
всіх векторів деякої площини і деякої
прямої відносно операцій додавання
векторів і множення векторів на число
також є дійсними векторними просторами.
Позначимо їх відповідно
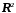 і
і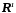 .
.
3)
Сукупність
 всіх матриць розмірності
всіх матриць розмірності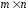 з дійсними елементами утворює дійсний
векторний простір відносно операцій
додавання матриць і множення матриць
на число.
з дійсними елементами утворює дійсний
векторний простір відносно операцій
додавання матриць і множення матриць
на число.
4)
Множина всіх векторів – розв’язків
однорідної системи лінійних алгебраїчних
рівнянь з коефіцієнтами з поля
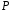 відносно операцій додавання векторів
і множення вектора на число з поля
відносно операцій додавання векторів
і множення вектора на число з поля .
.
5)
 -вимірний
арифметичний (координатний) простір
над полем
-вимірний
арифметичний (координатний) простір
над полем
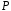 – множина
– множина
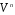 всіх
всіх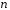 -вимірних
числових векторів
-вимірних
числових векторів
 з компонентами з поля
з компонентами з поля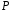 ,
тобто впорядкованих наборів з
,
тобто впорядкованих наборів з
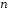 чисел
чисел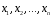 з поля
з поля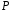 разом з операціями додавання векторів
і множення вектора на число з поля
разом з операціями додавання векторів
і множення вектора на число з поля ,
для яких виконуються всі властивості
лінійних дій над векторами.
,
для яких виконуються всі властивості
лінійних дій над векторами.
6)
Сукупність
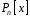 всіх многочленів від змінної
всіх многочленів від змінної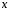 степеня не вище
степеня не вище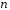 з дійсними коефіцієнтами відносно
операцій додавання многочленів і
множення многочленів на число утворює
дійсний векторний простір.
з дійсними коефіцієнтами відносно
операцій додавання многочленів і
множення многочленів на число утворює
дійсний векторний простір.
7)
Сукупність всіх неперервних функцій
дійсної змінної, які визначені на деякому
проміжку
 ,
утворює дійсний векторний простір
відносно операцій додавання функцій і
множення функцій на число. Роль
нуль-вектора відіграє функція, яка
тотожно дорівнює нулю.
,
утворює дійсний векторний простір
відносно операцій додавання функцій і
множення функцій на число. Роль
нуль-вектора відіграє функція, яка
тотожно дорівнює нулю.
З означення безпосередньо випливають наступні
Найпростіші властивості векторного простору:
1) Єдиність
нульового вектора. В
векторному просторі
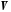 існує єдиний нульовий вектор, тобто
такий, що
існує єдиний нульовий вектор, тобто
такий, що :
:
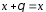 .
(аксіома 3)
.
(аксіома 3)
2)
Єдиність
протилежного елемента. В
векторному просторі
 для будь-якого вектора
для будь-якого вектора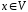 існує
єдиний вектор
існує
єдиний вектор
 такий,
що
такий,
що
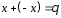 .
(аксіома 4)
.
(аксіома 4)
3) Для будь-якого
вектора
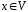
 .
.
4)
Для будь-якого числа
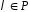 і
і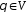
 .
.
5)
Якщо добуток
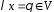 ,
то або
,
то або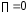 ,
або
,
або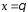 .
.
6)
Для будь-якого вектора
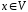 елемент
елемент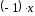 є протилежним до
є протилежним до .
.
2. Лінійна залежність системи векторів
Вектор
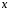 називається пропорціональним вектору
називається пропорціональним вектору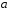 ,
якщо для деякого числа
,
якщо для деякого числа
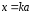 .
В аналітичній геометрії такі вектори
називалися колінеарними.
.
В аналітичній геометрії такі вектори
називалися колінеарними.
Означення.
Лінійною
комбінацією
векторів
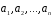 векторного простору
векторного простору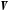 називається вектор
називається вектор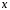 вигляду
вигляду
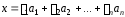 .(1)
.(1)
де
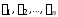 – деякі числа з поля
– деякі числа з поля (коефіцієнти лінійної комбінації).Якщо
вектор
(коефіцієнти лінійної комбінації).Якщо
вектор
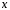 записаний у вигляді (1), то кажуть, що вінрозкладений
за системою векторів
записаний у вигляді (1), то кажуть, що вінрозкладений
за системою векторів
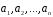 ,
або що він лінійно
виражається через вектори
,
або що він лінійно
виражається через вектори
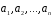 .
.
Означення.
Система векторів
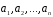 векторного простору
векторного простору називаєтьсялінійно
залежною,
якщо існують числа
називаєтьсялінійно
залежною,
якщо існують числа
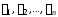 ,
які не всі водночас дорівнюють нулю
(
,
які не всі водночас дорівнюють нулю
(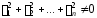 ),
такі що
),
такі що
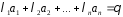 (2)
(2)
Система
векторів
 називаєтьсялінійно
незалежною,
якщо остання рівність виконується
тільки в одному випадку, коли
називаєтьсялінійно
незалежною,
якщо остання рівність виконується
тільки в одному випадку, коли
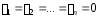 .
.
Теорема
(про лінійну залежність векторів).
Вектори
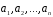 лінійно залежні тоді і тільки тоді, коли
один з векторів цієї системи є лінійною
комбінацією інших.
лінійно залежні тоді і тільки тоді, коли
один з векторів цієї системи є лінійною
комбінацією інших.
Приклади лінійно залежних і лінійно незалежних систем векторів.
1)
У векторному просторі комплексних чисел
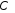 вектори
вектори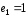 і
і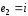 утворюють лінійно незалежну систему.
утворюють лінійно незалежну систему.
2)
В арифметичному числовому векторному
просторі
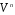 система одиничних векторів
система одиничних векторів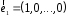 ,
, ,…,
,…,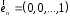 лінійно незалежна.
лінійно незалежна.
3)
У векторному просторі
 геометричних векторів будь-які чотири
вектори лінійно залежні, а будь-які три
некомпланарні вектори лінійно незалежні.
геометричних векторів будь-які чотири
вектори лінійно залежні, а будь-які три
некомпланарні вектори лінійно незалежні.
Аналогічно,
у векторному просторі
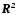 будь-які три вектори лінійно залежні,
а будь-які два неколінеарні вектори
лінійно незалежні.
будь-які три вектори лінійно залежні,
а будь-які два неколінеарні вектори
лінійно незалежні.
4)
У векторному просторі всіх многочленів
від змінної
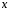 з дійсними коефіцієнтами многочлени
з дійсними коефіцієнтами многочлени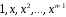 лінійно
незалежні.
лінійно
незалежні.
5) У векторному
просторі всіх неперервних функцій
дійсної змінної на числовій прямій
система функцій
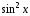 ,
, ,
1 лінійно залежна, оскільки
,
1 лінійно залежна, оскільки
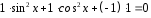 .
.
(Як
відомо, функція 1 є лінійною комбінацією
функцій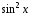 і
і :
:
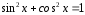 ).
).
Теорема (про лінійну залежність системи векторів). Якщо деяка підсистема заданої системи векторів лінійно залежна, то і вся система векторів лінійно залежна.
Наслідок 1. Скінченна система векторів, яка містить нульовий вектор, лінійно залежна.
Наслідок 2. Скінченна система векторів, яка містить пропорціональні вектори, лінійно залежна.
Наслідок 3. Якщо система векторів лінійно незалежна, то будь-яка її підсистема лінійно незалежна.
Означення.
Кажуть, що
система векторів
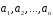 лінійно виражається через систему
векторів
лінійно виражається через систему
векторів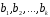 ,
якщо кожен вектор системи
,
якщо кожен вектор системи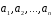 лінійно виражається через вектори
лінійно виражається через вектори .
.
Означення. Дві скінченні системи векторів називаються еквівалентними, якщо вони лінійно виражаються одна через одну.
Теорема
(Основна теорема про лінійну залежність
векторів).
Нехай задані дві системи векторів
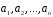 і
і ,
причому перша лінійно незалежна і
лінійно виражається через другу. Тоді
число векторів в першій системі не
перебільшує числа векторів в другій,
тобто
,
причому перша лінійно незалежна і
лінійно виражається через другу. Тоді
число векторів в першій системі не
перебільшує числа векторів в другій,
тобто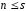 .
.
Наслідок. Будь-які дві еквівалентні лінійно незалежні системи векторів мають однакове число векторів.
Означення. Базисом системи векторів називається будь-яка її максимальна лінійно незалежна підсистема. Число векторів в базисі називається рангом системи векторів.
Теорема
(про ранги двох систем векторів).
Нехай задані дві системи векторів,
причому ранг першої дорівнює
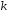 ,
а ранг другої дорівнює
,
а ранг другої дорівнює .
Якщо перша система лінійно виражається
через другу, то
.
Якщо перша система лінійно виражається
через другу, то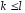 .
Якщо дві системи еквівалентні, то
.
Якщо дві системи еквівалентні, то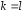 .
.
