
- •Лекція 1 Тема: Скінченновимірні векторні простори
- •1. Поняття, приклади і найпростіші властивості векторного простору над полем
- •3. Ранг матриці
- •4. Базис і розмірність векторного простору
- •5. Координати вектора у векторному просторі. Розкладання вектора за базисом
- •2) Розкладемо вектор за базисом:
- •Розв’язуючи цю систему будь-яким способом, знайдемо , ,.
- •6. Ізоморфізм векторних просторів
- •7. Системи лінійних алгебраїчних рівнянь (загальна теорія)
- •Слар сумісна .
- •Слар має єдиний розв’язок
- •Слар має безліч розв’язків
- •8. Підпростори векторного простору
3. Ранг матриці
Розглянемо довільну
матрицю
 розмірності
розмірності
 :
:

Будемо дивитися
на рядки матриці
 як на вектори арифметичного числового
векторного простору
як на вектори арифметичного числового
векторного простору ,
а на саму матрицю – як на скінченну
систему векторів.
,
а на саму матрицю – як на скінченну
систему векторів.
Означення.
Рангом
матриці
 називається
ранг
системи рядків матриці
називається
ранг
системи рядків матриці
 .
.
З
означення рангу системи векторів
випливає, що ранг матриці дорівнює
максимальному
числу
лінійно незалежних рядків.
Позначається ранг матриці
 .
.
Оскільки максимальна лінійно незалежна підсистема рядків матриці утворює базис системи всіх рядків, то такі рядки називають базисними рядками.
Ранг матриці
 можна також визначити як ранг системи
її стовпців. Ясно, ранг системи рядків
матриці
можна також визначити як ранг системи
її стовпців. Ясно, ранг системи рядків
матриці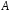 збігається з рангом системи стовпців
матриці
збігається з рангом системи стовпців
матриці .
.
Відзначимо деякі властивості рангу матриці:
1. Ранг матриці не змінюється при її транспонуванні.
2. Ранг матриці не змінюється при множенні всіх елементів деякого рядка (стовпця) на ненульове число.
4. Ранг матриці не змінюється при елементарних перетвореннях рядків (стовпців).
Згадаємо, що елементарними перетвореннями матриці називаються такі перетворення:
переставлення двох рядків (стовпців);
множення рядка (стовпця) на довільне дійсне число, відмінне від 0 ;
додавання до одного рядка (стовпця) іншого рядка (стовпця) помноженого на довільне дійсне число;
викреслювання або дописування нульового рядка (стовпця).
Сформульовані властивості вказують можливий шлях обчислення рангу матриці. Щоб обчислити ранг матриці, треба спростити її за допомогою елементарних перетворень так, щоб висновок про ранг став очевидним.
Приклад. Обчислити ранг матриці за допомогою елементарних перетворень:


4. Базис і розмірність векторного простору
Означення.
Базисом
векторного простору
 називається така впорядкована система
векторів
називається така впорядкована система
векторів ,
що
,
що
1) вона лінійно незалежна;
2)
кожен вектор
 простору
простору лінійно виражається через вектори цієї
системи, тобто
лінійно виражається через вектори цієї
системи, тобто .
.
Зауваження.
Якщо в базисі
 змінити порядок векторів, то отримаємо
інший базис, хоч він і складається з тих
самих векторів. Ясно, що для даного
простору базис можна вибрати не єдиним
чином.
змінити порядок векторів, то отримаємо
інший базис, хоч він і складається з тих
самих векторів. Ясно, що для даного
простору базис можна вибрати не єдиним
чином.
Приклади базисів.
1)
У векторному просторі комплексних чисел
 вектори
вектори і
і утворюють базис, оскільки вони лінійно
незалежні і довільне комплексне число
утворюють базис, оскільки вони лінійно
незалежні і довільне комплексне число лінійно через них виражається.
лінійно через них виражається.
2)
В арифметичному числовому векторному
просторі
 система одиничних векторів
система одиничних векторів ,
, ,…,
,…, утворює базис.
утворює базис.
3)
У векторному просторі
 геометричних векторів будь-які три
некомпланарні вектори утворюють базис.
Зокрема, базис утворює трійка ортів
геометричних векторів будь-які три
некомпланарні вектори утворюють базис.
Зокрема, базис утворює трійка ортів .
.
Аналогічно,
у векторному просторі
 будь-які два неколінеарні вектори
утворюють базис. Зокрема, базис утворює
пара ортів
будь-які два неколінеарні вектори
утворюють базис. Зокрема, базис утворює
пара ортів .
.
У
векторному просторі
 базис утворює будь-який вектор, напрям
якого збігається з напрямом осі.
базис утворює будь-який вектор, напрям
якого збігається з напрямом осі.
4) У векторному
просторі всіх многочленів від змінної
 з дійсними коефіцієнтами многочлени
з дійсними коефіцієнтами многочлени утворюють базис, оскільки вони лінійно
незалежні і довільний многочлен
утворюють базис, оскільки вони лінійно
незалежні і довільний многочлен -го
степеня може бути виражений у вигляді
-го
степеня може бути виражений у вигляді
 .
.
Означення.
Векторний простір
 називається
називається -вимірним,
якщо в ньому існує базис з
-вимірним,
якщо в ньому існує базис з
 елементів. Число
елементів. Число називаєтьсярозмірністю
простору і позначається
називаєтьсярозмірністю
простору і позначається
 .
Простір скінченної розмірності
називається скінченновимірним.
Простір, в якому можна знайти будь-яке
число лінійно незалежних векторів
називається нескінченновимірним.
.
Простір скінченної розмірності
називається скінченновимірним.
Простір, в якому можна знайти будь-яке
число лінійно незалежних векторів
називається нескінченновимірним.
Отже, розмірність векторного простору – це максимальне число лінійно незалежних векторів цього простору.
Приклади.
1)
 ,
, .
.
2)
 .
.
3)
 .
.
4) Векторний простір функцій, визначений на числовій прямій, нескінченновимірний.
Теорема
(про зв'язок між базисом і розмірністю).
Система векторів
 утворює в просторі
утворює в просторі розмірності
розмірності базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору
базис тоді і тільки тоді, коли вона
лінійно незалежна, а число векторів в
ній дорівнює розмірності простору .
.
