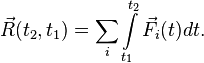Динамика билеты / 14Теория об изменении количества движения и момента

В качестве системы, о которой идёт речь в теореме, может выступать любая механическая система, состоящая из любых тел.

Формулировка теоремы

Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы.

( кг·м/с )

Теорема об изменении количества движения системы утверждает

Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени.

Закон сохранения количества движения системы

Если сумма всех внешних сил, действующих на систему, равна нулю, то количество движения (импульс) системы есть величина постоянная.

Введя в рассмотрение изменение импульса внешних сил , получим выражение теоремы об изменении количества движения системы в дифференциальной форме:

Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми  и , получим выражение теоремы об изменении количества движения системы в интегральной форме:

где  и  — значения количества движения системы в моменты времени  и  соответственно, а  — импульс внешних сил за промежуток времени . В соответствии со сказанным ранее и введёнными обозначениями выполняется

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

(моме́нт коли́чества движе́ния м²·кг·с⁻¹ )

Теорема об изменении момента количества движения относительно центра

производная по времени от момента количества движения (кинетического момента) материальной точки относительно какого-либо неподвижного центра равна моменту действующей на точку силы относительно того же центра. 

dk₀/dt = M₀(F).                                          

Теорема об изменении момента количества движения относительно оси

производная по времени от момента количества движения (кинетического момента) материальной точки относительно какой-либо неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.

   dk_x/dt = M_x(F);   dk_y/dt = M_y(F);   dk_z/dt = M_z(F).            

Рассмотрим материальную точку M массой m , движущуюся под действием силы F(рисунок 3.1). Запишем и построим вектор момента количества движения (кинетического момента) M₀ материальной точки относительно центра O:

Дифференцируем выражение момента количества движения (кинетического момента k₀ ) по времени:

        Так как dr/dt = V, то векторное произведение V ⊗ m⋅V(коллинеарных векторов V и m⋅V ) равно нулю. В то же время d(m⋅V)/dt = F согласно теореме о количестве движения материальной точки. Поэтому получаем, что 

                                            dk₀/dt = r⊗F,                                            (3.3)

где r⊗F = M₀(F) – вектор-момент силы F относительно неподвижного центра O. Вектор k₀ ⊥ плоскости (r,m⊗V ), а вектор M₀(F) ⊥ плоскости (r,F ), окончательно имеем

                                            dk₀/dt = M₀(F).                                           (3.4)

 Уравнение (3.4)  выражает теорему об изменении момента количества движения (кинетического момента) материальной точки относительно центра: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какого-либо неподвижного центра равна моменту действующей на точку силы относительно того же центра. 

Проецируя равенство (3.4) на оси декартовых координат, получаем

             dk_x/dt = M_x(F);   dk_y/dt = M_y(F);   dk_z/dt = M_z(F).             (3.5)  

         Равенства (3.5) выражают теорему об изменении момента количества движения (кинетического момента) материальной точки относительно оси: производная по времени от момента количества движения (кинетического момента) материальной точки относительно какой-либо неподвижной оси равна моменту действующей на эту точку силы относительно той же оси.

         Рассмотрим следствия, вытекающие из теорем (3.4) и (3.5).

         Следствие 1. Рассмотрим случай, когда сила F во все время движения точки проходит через неподвижный центр O (случай центральной силы), т.е. когда M₀(F) = 0. Тогда из теоремы (3.4) следует, что k₀ = const,

         т.е. в случае центральной силы момент количества движения (кинетический момент) материальной точки относительно центра этой силы остается постоянным по модулю и направлению (рисунок 3.2).

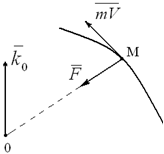
Рисунок 3.2

         Из условия k₀ = const следует, что траектория движущейся точки представляет собой плоскую кривую, плоскость которой проходит через центр этой силы.

         Следствие 2. Пусть M_z(F) = 0, т.е. сила пересекает ось z или ей параллельна. В этом случае, как это видно из третьего из уравнений (3.5), k_z = const,

         т.е. если момент действующей на точку силы относительно какой-либо неподвижной оси всегда равен нулю, то момент количества движения (кинетический момент) точки относительно этой оси остается постоянным.

Доказательство теоремы обь ихменении количества движения

Пусть система состоит из  материальных точек с массами  и ускорениями . Все силы, действующие на тела системы, разделим на два вида:

Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим .

Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать , а силу воздействия i-й точки на k-ю точку — . Очевидно, что при , то 

Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде

Учитывая, что  и суммируя все уравнения второго закона Ньютона, получаем:

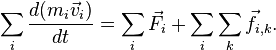
Выражение  представляет собой сумму всех внутренних сил, действующих в системе. По третьему закону Ньютона в этой сумме каждой силе  соответствует сила  такая, что  и, значит, выполняется  Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать

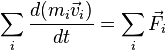
Используя для количества движения системы  обозначение , получим

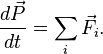
Введя в рассмотрение изменение импульса внешних сил , получим выражение теоремы об изменении количества движения системы в дифференциальной форме:

Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми  и , получим выражение теоремы об изменении количества движения системы в интегральной форме:

где  и  — значения количества движения системы в моменты времени  и  соответственно, а  — импульс внешних сил за промежуток времени . В соответствии со сказанным ранее и введёнными обозначениями выполняется