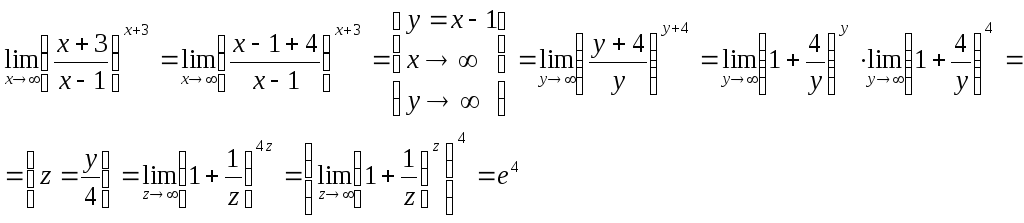- •1. Границя послідовності
- •1.1. Числова послідовність
- •1.2. Обмежені й необмежені послідовності
- •1.3. Монотонні послідовності
- •1.4. Число е
- •2. Границя функції
- •Геометричний зміст границі функції у точці
- •Геометричний зміст границі функції у нескінченності
- •2.1. Властивості нескінченно малих функцій
- •2.2. Порівняння нескінченно малих функцій
- •2.3. Властивості еквівалентних нескінченно малих
- •2.4. Теореми про границі
- •3. Методичні рекомендації
- •4. Індивідуальні завдання Знайти границі
2.4. Теореми про границі
Практичне обчислення границь базується на наступних теоремах про границі: якщо існують
![]() та
та
![]() ,
то:
,
то:
1.
![]() ,
де С = const.
,
де С = const.
2.
![]() =
=![]() ,
де С = const.
,
де С = const.
3.
![]() =
=![]()
![]()
![]() .
.
4.
![]() =
=![]()
![]() .
.
5.
![]() =
= ,
де (
,
де (![]()
![]() ).
).
А також на теоремах
про граничний перехід під знаком
неперервної функції: якщо
![]() неперервна у точці
неперервна у точці![]() та
та![]() ,
то
,
то
![]() .
.
3. Методичні рекомендації
На практиці для обчислення границь велике значення мають такі границі:
1.
![]() (перша
визначна границя).
(перша
визначна границя).
2.
![]() (друга
визначна границя).
(друга
визначна границя).
3.
![]() ,
,
де P(x) = a0xn + a1xn-1 +…+an, Q(x) =b0xm+b1xm-1+…+bm – багаточлени.
 ;
;
 .
.

Разом:

Крім цього, можна записати наступні корисні на практиці співвідношення:

![]()
Якщо функція є
елементарною та якщо граничне значення
аргументу належить до її області
визначення, то обчислення границі
зводиться до простої підстановки
граничного значення аргументу. Тобто
границя елементарної функції
![]() при
при![]() наближається до значення
наближається до значення![]() ,
яке входить до області визначення
функції, дорівнює приватному значенню
функції при
,
яке входить до області визначення
функції, дорівнює приватному значенню
функції при![]() :
:
![]() .
.
Розглянемо випадки,
коли границю функції не можна визначити
шляхом підстановки замість аргументу
його граничного значення (невизначеності
![]() ,(
,(![]() ),
),![]() ,
,![]() ,
,![]() ).
У цих випадках необхідно проводити
додаткові дослідження, основані на
тотожних перетвореннях функції.
).
У цих випадках необхідно проводити
додаткові дослідження, основані на
тотожних перетвореннях функції.
Випадок, коли функція, яка стоїть під знаком границі при
 або
або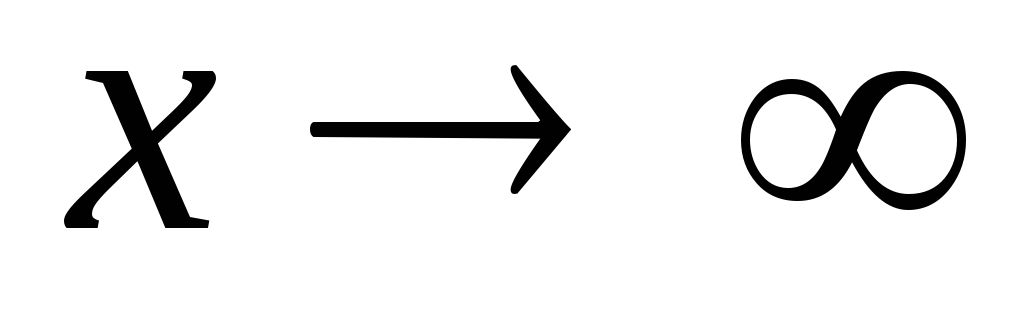 ,
– це відношення двох нескінченно
великих величин (невизначеність типу
,
– це відношення двох нескінченно
великих величин (невизначеність типу ).
).
Тобто
![]() ,
,![]() =
=![]() .
.
Якщо
![]() та
та![]() – раціональні функції, то числівник та
знаменник дробу необхідно розділити
на найвищий степінь
– раціональні функції, то числівник та
знаменник дробу необхідно розділити
на найвищий степінь![]() , який зустрічається в доданках числівника
та знаменника.
, який зустрічається в доданках числівника
та знаменника.
Приклад. Знайти границю
![]() .
.
Спочатку переконуємось
у тому, що маємо невизначеність
![]() ,
зробимо деякі перетворення. Розділимо
числівник і знаменник на
,
зробимо деякі перетворення. Розділимо
числівник і знаменник на![]() (найбільший степінь числівника та
знаменника):
(найбільший степінь числівника та
знаменника):
![]() =
=![]() =
= .
.
Приклад. Знайти границю
![]() .
.
Спочатку
переконуємось, що маємо невизначеність
![]() ,
розділимо числівник і знаменник на
,
розділимо числівник і знаменник на![]() (найбільший степінь числівника та
знаменника):
(найбільший степінь числівника та
знаменника):
![]() =
=![]() =
= .
.
Випадок, коли функція, яка стоїть під знаком границі при
 або
або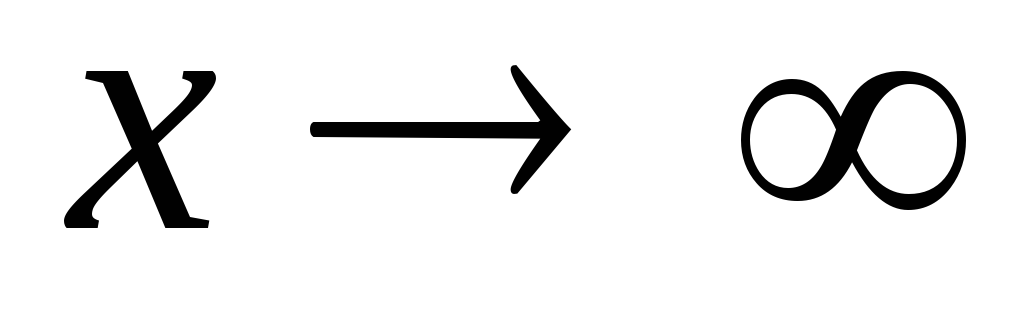 ,
– це відношення двох нескінченно малих
величин (невизначеність типу
,
– це відношення двох нескінченно малих
величин (невизначеність типу ).
).
Тобто
![]() ,
,![]() =
=![]() .
.
У цьому випадку шляхом тотожних алгебраїчних або тригонометричних перетворень необхідно скоротити дріб.
Приклад. Знайти границю
![]() .
.
Спочатку переконуємось
у тому, що маємо невизначеність типу
![]() ,
зробимо деякі перетворення, а саме:
,
зробимо деякі перетворення, а саме:
![]() =
=![]() =
=![]()
![]() .
.
Приклад. Знайти границю
![]() .
.
Приклад. Знайти границю
 .
.
Приклад.
Знайти границю
![]() .
.
Розкладемо чисельник і знаменник на множники.
x2 – 3x + 2 = (x – 1)(x – 2).
Таким чином, можна записати x2 – 5x + 6 = (x – 2)(x – 3),тому що
 x3–
6x2+ 11x – 6 x - 1
x3–
6x2+ 11x – 6 x - 1
x3– x2x2– 5x + 6.
- 5x2+ 11x
- 5x2+ 5x
6x - 6
6x - 6 0
Тоді
![]() .
.
Випадок, коли функція, яка стоїть під знаком границі при
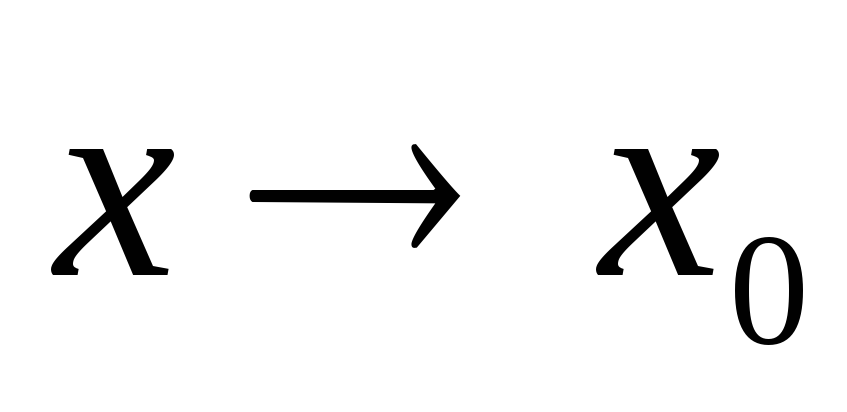 або
або ,
– це різниця двох нескінченно великих
величин (невизначеність типу
,
– це різниця двох нескінченно великих
величин (невизначеність типу
 ).
).
Тобто
![]() ,
,![]() =
=![]()
![]() .
.
Цей випадок
невизначеності можна привести до
розглянутих раніше випадків
![]() ,
,![]() шляхом перетворення функції.
шляхом перетворення функції.
Приклад.
Знайти границю
![]() – невизначеність типу (
– невизначеність типу (![]() ).
).
![]() =
=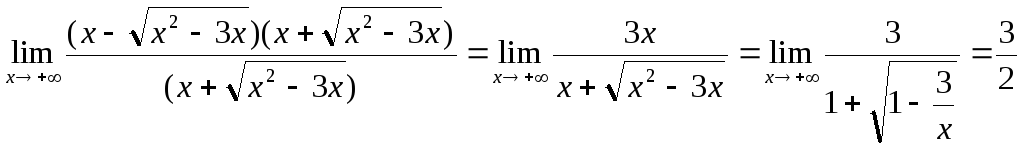 .
.
Випадок, коли при
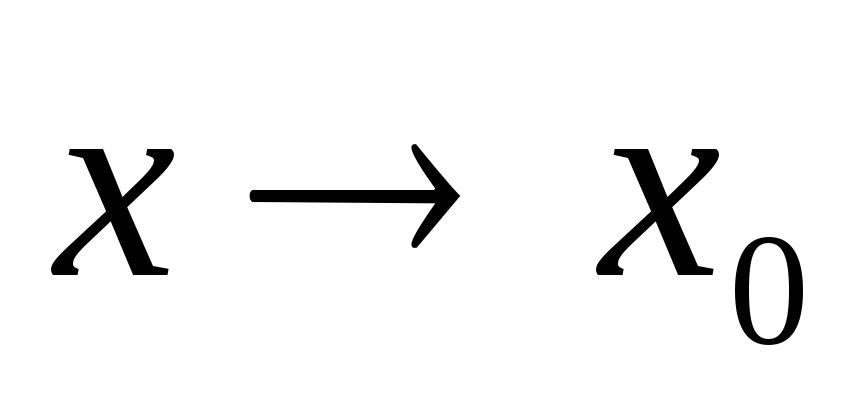 або
або функція,
яка стоїть під знаком границі, – це
добуток нескінченно малої величини на
нескінченно велику (невизначеність
типу
функція,
яка стоїть під знаком границі, – це
добуток нескінченно малої величини на
нескінченно велику (невизначеність
типу
 ).
).
Тобто
![]() ,
,![]() =0,
=0,
![]()
![]() .
.
Цей випадок, як і
попередній, можна привести до розглянутих
раніше випадків невизначеностей типів
![]() ,
,![]() .
.
Приклад.
Знайти границю
![]() ,
,
маємо
невизначеність типу (![]() ).
Нехай
).
Нехай![]() ,
тоді отримаємо:
,
тоді отримаємо:
![]() =
=![]()
![]() .
.
Випадок, коли при
 або
або функція,
яка стоїть під знаком границі, – це
степінь, основа якого наближається до
одиниці, а показник – до нескінченності
(невизначеність типу
функція,
яка стоїть під знаком границі, – це
степінь, основа якого наближається до
одиниці, а показник – до нескінченності
(невизначеність типу
 ).
).
Тобто
![]() ,
,![]() =1,
=1,![]() =
=![]() .
У цьому випадку знаходження границі
зводиться до другої визначної границі.
.
У цьому випадку знаходження границі
зводиться до другої визначної границі.
Приклад. Знайти границю
![]()
![]() =
=![]() =
=![]() =
=
=![]()
![]() =
=![]() .
.
Приклад. Знайти границю.