
2.3.2. Графічне відображення оптимізації
Процес пошуку оптимального стану об’єкта можна наочно відобразити графічним способом, якщо кількість оптимізуємих параметрів F – один або два .
В одновимірній оптимізації (F=1) залежність критерія оптимальності Ф від значення єдиного оптимізуємого параметра х можна відобразити простим графіком залежності Ф(х), який матиме мінімум або максимум.
В двовимірних задачах цільову функцію Ф(х1,х2) можна відобразити як двовимірну поверхню в координатній системі ( Ф,х1,х2). На площині таку поверхню простіше зображувати горизонтальними перетинами, які мають назву «ізолінії Ф=const». Це лінії, на кожній з яких значення критерія Ф залишається постійним. Якщо екстремум один, тоді система ізоліній матиме вигляд концентричних замкнутих ліній, вкладених одна в другу. Аналогічні ізолінії однакових висот чи глибин рисують на географічних картах.

Рис. 2.3.1. а- Графічне зображення поверхні цільової функції Ф(х1,х2)), б– проекції її горизонтальних перетинів (ізоліній Ф=const) на координатну площину (х1,х2).
Алгоритми оптимізації
Всі алгоритми оптимізації (а їх існує велика кількість) зводяться до виконання деякої ітераційної (повторюваної) процедури, кожний крок якої складається з послідовності таких операцій:
Обирається за певним правилом деяка конкретна комбінація значень оптимізуємих параметрів х1, х2,..хF (попередній стан об’єкта) і значення всіх 1…m параметрів змінюються на величину кроку х ( наступний стан) :
![]() 2.3.3)
2.3.3)
де верхній індекс n означає номер кроку , нижній - номер параметра в списку.
Правилами вибору наступного стану якраз і відрізняються різні алгоритми
Виконується розрахунок на математичній моделі значень вихідних параметрів Y1, Y2,Y3…YN та підраховується значення критерія оптимальності Ф ;
Значення критерія оптимальності, підраховане на крокові «М» (ФM), порівнюється зі значеннями критерія Ф на попередніх найближчих кроках (ФM-1, ФM-2,…), одним або декількома, і з цих даних робиться висновок про те, в якому напрямку слід зробити наступний крок (тобто як змінити значення всіх оптимізуємих параметрів і перевести об’єкт в новий стан, більш близький до оптимального).
В залежності від способу вибору напрямку кроку х методи оптимізації можна розподілити на дві групи – градієнтні та без градієнтні.
Градієнтні методи засновані на підрахуванні та аналізі часткових похідних критерія оптимальності за параметрами х1,….хm:
![]() (2.3.4)
(2.3.4)
Кожна похідна підраховується за значеннями критерія оптимальності Ф в двох точках – хn та хn+1. Знак та величина похідної показують, наближується чи віддалюється значення критерія Ф від екстремуму при виконанні одного кроку. В формулі (2.3.4) похідна виражена приблизним дискретним (різницевим) способом, тому чим меншим буде крок хm , тим точнішим буде значення похідної, але тим більше кроків потрібно виконати до досягнення екстремуму функції Ф(х1,х2..). В алгоритмах часто спочатку крок обирають великим, а в процесі пошуку при наближенні до екстремуму поступово зменшують.
Значення параметрів х1, х2,.. – це числа з різними розмірностями, які неможливо порівнювати між собою. До того ж числа можуть набагато відрізнятись між собою за величиною. Тому в градієнтних методах значення параметрів потрібно нормалізувати, тобто представити у безрозмірній формі з інтервалом коливань 0…1. Нормалізація виконується діленням розмірного значення параметра хn на різницю між найбільшим і найменшим розмірним значеннями (інтервал змінювання в задачі) :
![]() . (2.3.5)
. (2.3.5)
Розглянемо декілька прикладів градієнтних методів .
Метод релаксації
.
Спочатку підраховують всі часткові
похідні по змінним х
(dF/dx1,
і
dF/dx2),
і
вибирають ту змінну (наприклад, х1)
, у якої модуль похідної
![]() максимальний,
тобто найшвидше змінюється критерій
Ф. Саме в напрямку цієї координати х1
і рухаються, змінюючи лише один цей
параметр. Рух продовжується до того
моменту, коли буде знайдено найбільше
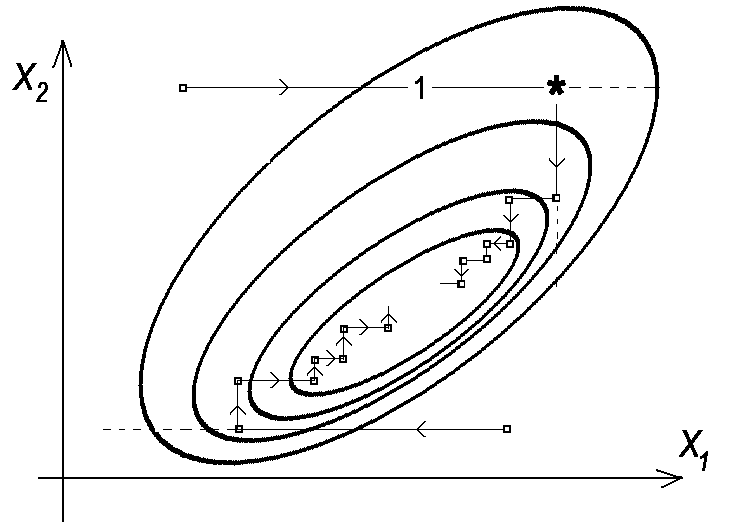
значення критерія Ф (точка * на рис.2.3.2.а
на лінії руху 1). В точці максимуму
значення похідної
максимальний,
тобто найшвидше змінюється критерій
Ф. Саме в напрямку цієї координати х1
і рухаються, змінюючи лише один цей
параметр. Рух продовжується до того
моменту, коли буде знайдено найбільше
значення критерія Ф (точка * на рис.2.3.2.а
на лінії руху 1). В точці максимуму
значення похідної
![]() дорівнює нулю, і більшою за модулем
стає інша похідна, в двовимірній задачі
-
дорівнює нулю, і більшою за модулем
стає інша похідна, в двовимірній задачі
-![]() .
Зі знайденої точки максимуму (х1*)
функції Ф(х1)
починають рухатись в напрямку осі х2,
доки не буде знову знайдено максимальне
значення функції Ф(х2).
Далі всі операції повторюються. Якщо
таким чином змінювати по черзі напрям
руху, поступово стан зміщується до
оптимального від будь-якої початкової
точки.
.
Зі знайденої точки максимуму (х1*)
функції Ф(х1)
починають рухатись в напрямку осі х2,
доки не буде знову знайдено максимальне
значення функції Ф(х2).
Далі всі операції повторюються. Якщо
таким чином змінювати по черзі напрям
руху, поступово стан зміщується до
оптимального від будь-якої початкової
точки.
а б
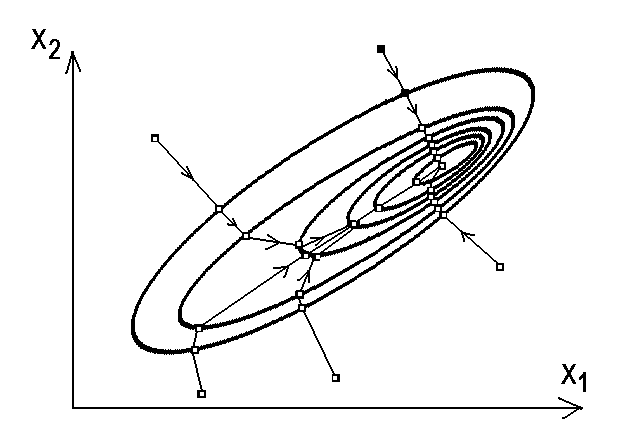
Рис.2.3.2. Траєкторії руху стану до оптимального з різних початкових точок в методі релаксації (а) та методі градієнта. (б)
Метод градієнта
відрізняється від релаксаційного тим,
що на кожному крокові одночасно
змінюються значення усіх параметрів,
кожний з них пропорційно модулю
відповідної часткової похідної,
![]() або
або![]() .
Тому напрямок руху буде співпадати з
напрямком вектора градієнта функції
Ф(х1,х2), тобто по найкоротшій траєкторії,
перпендикулярно до ізоліній Ф=const.
.
Тому напрямок руху буде співпадати з
напрямком вектора градієнта функції
Ф(х1,х2), тобто по найкоротшій траєкторії,
перпендикулярно до ізоліній Ф=const.
Метод найшвидшого спуску є комбінацією двох попередніх методів, який дещо зменшує недоліки обох – неоптимальну траєкторію пошуку в релаксаційному методі і необхідність підрахування всіх часткових похідних в методі градієнта. Тут також спочатку підраховують всі часткові похідні, обирають напрямок руху уздовж напрямку градієнта , і рухаються в цьому напрямку до того моменту, поки не зміниться знак приросту критерія оптимальності (Ф n+1 – Ф n ), тобто коли буде досягнуте екстремальне значення в цьому напрямку. В цій точці знову підраховують всі часткові похідні критерія Ф, обирають новий напрямок руху і рухаються до чергової точки екстремуму.
Безградієнтні методи засновані на порівнянні значень критерія оптимальності в результаті виконання декількох кроків і не вимагають підрахування часткових похідних.
Пошук екстремуму однієї змінної . Це найпростіша одновимірна задача. Вона зводиться до пошуку мінімуму чи максимуму на залежності Ф(х) в області визначення параметра х (інтервал між найменшим xMIN та найбільшим xMAX значеннями, обирається з окремих умов і є допустимим інтервалом коливань в регламентованій області ). Всі алгоритми зводяться до того, щоб відокремити менший інтервал, в якому і знаходиться екстремум.
Простий, хоч і не оптимальний метод полягає в тому, щоб начати рух з будь-якої точки всередині заданої області, і рухатись у довільно обраному напрямку , якщо при цьому критерій Ф змінюється монотонно у потрібному напрямку (зростає при пошуку максимуму або зменшується при пошуку мінімуму). Рух продовжується до того моменту, коли критерій Ф на наступному крокові змінився в протилежному напрямку, тобто точка екстремуму пройдена. Тоді напрямок руху змінюють на зворотний, а величину кроку х зменшують.
Початковий крок обирають спочатку великим, а при кожній зміні напрямку руху зменшують на деяку величину. Траєкторія пошуку мінімуму нагадує рух кульки, яка скочується під дією сили тяжіння по лінії Ф(х) , здійснює декілька затухаючих коливань в обидва боки і зупиняється в точці мінімуму.
Метод симплексів. Симплексом називають геометричну фігуру (опуклий багатогранник), утворену точками в координатному просторі х1, х2,…хF. Кількість вершин багатогранника на одиницю більша кількості ступенів свободи F оптимізаційної задачі. Якщо оптимізованих параметрів два, тоді симплекс являє собою рівносторонній трикутник (рис. 2.3.3).
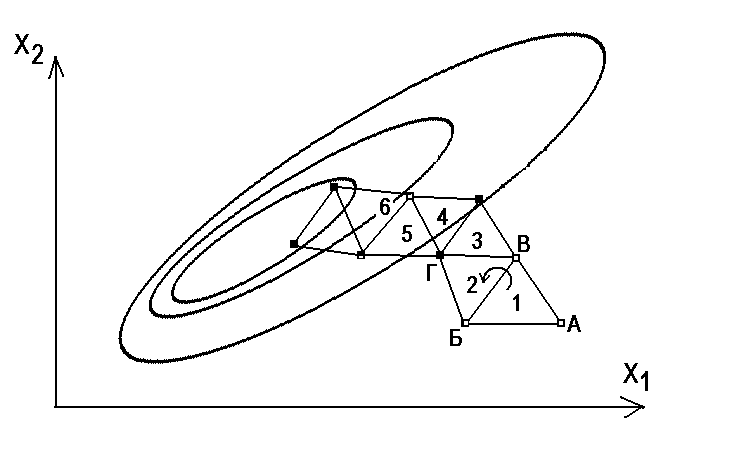
Рис. 2.3.3. Траєкторія пошуку екстремуму симплексним методом.
Перший симплекс (1) з вершинами А,Б,В будують довільно. Далі визначають значення критерія Ф в трьох точках (вершинах) симплекса і порівнюють їх між собою та знаходять найгірше значення Ф, тобто найвіддаленіше від екстремуму (на рисунку 2.3.3. це вершина А). Наступний симплекс (2) будують, використовуючи дві інші вершини першого (Б,В). Третьою вершиною симплекса 2 має бути точка, симетрична «найгіршій» вершині А у першому симплексі. Можна уявити собі процедуру побудови кожного наступного симплекса (2) як поворот симплекса АБВ кругом осі БВ. Відомо, що така процедура послідовного руху по вершинах симплексів приводить до екстремуму.
Приклад одновимірної оптимізаційної задачі
Розглянемо
хімічне джерело струму (ХДС), на якому
вимірюють три функціональних параметри
– струм І
А, напругу U
В, потужність
![]() Вт. З останньої формули видно, що
нульове значення потужності буде приІ=0
(ліва межа залежності потужності від
струму) і при струмі короткого замикання
, коли напруга дорівнює нулю, U=0.
Ця точка на графіку є в даному випадку
правою межею дозволеної області, бо
далі значення напруги ХДС будуть
негативними. Таким чином, залежність
потужності від струму повинна мати
вигляд опуклої лінії з максимумом
між крайніми нульовими значеннями.
Вт. З останньої формули видно, що
нульове значення потужності буде приІ=0
(ліва межа залежності потужності від
струму) і при струмі короткого замикання
, коли напруга дорівнює нулю, U=0.
Ця точка на графіку є в даному випадку
правою межею дозволеної області, бо
далі значення напруги ХДС будуть
негативними. Таким чином, залежність
потужності від струму повинна мати
вигляд опуклої лінії з максимумом
між крайніми нульовими значеннями.
Математичну
модель функціонування ХДС можна
записати як рівняння вольт-амперної
характеристики
![]() ,
а вираз для визначення критерія
оптимальності – це формула
,
а вираз для визначення критерія
оптимальності – це формула![]() ,
де перший множник – вхідний параметр
(незалежно регульований параметр в
гальваностатичній схемі експерименту),
другий – вихідний результат експерименту.
Експеримент полягає в тому, щоб задати
будь-яке значення струму розряду ХДС
і виміряти напругу.
,
де перший множник – вхідний параметр
(незалежно регульований параметр в
гальваностатичній схемі експерименту),
другий – вихідний результат експерименту.
Експеримент полягає в тому, щоб задати
будь-яке значення струму розряду ХДС
і виміряти напругу.
Побудуємо простий алгоритм пошуку оптимального струму, при якому спостерігається максимальне значення потужності. Для спрощення аналізу приймемо лінійну форму залежності напруги від струму U= U0-2I. Тут легко підрахувати праву межу дозволеної області існування станів ХДС – струм короткого замикання при U=0: ІКЗ= U0 /2
На рис. 2.3.4 показана графічна схема пошуку, реалізована в наведеному далі фрагменті програми. Інтервал пошуку екстремуму обмежений значеннями ІMIN=0 та ІMAX= ІКЗ=1А.
Процедура починається з будь-якої точки по осі вхідного параметра І. В даному випадку обрано значення І= dI*3 на початку вольт-амперної характеристики, де dI- початкове значення кроку пошуку. Пошук небажано починати з нульової точки, бо тоді перший крок вліво буде помилковим і реакція на нього ускладнить програму.
Вирішення математичної моделі і підрахунок критерія оптимальності Р в програмі організовані в формі окремої підпрограми mMOD, яка спрацьовує на кожному крокові пошуку.
Кожний крок пошуку в циклі k:=1 to 100 починається з установлення нового значення струму І оператором I:=I+dI та визначення критерія Р підпрограмою mMOD. Далі йде найважливіша частина алгоритму – логічний аналіз результату чергового кроку (досліду, виконаного на математичній моделі) та прийняття рішення про те, в який стан перевести ХДС, щоб наблизити його до оптимального. В даному випадку порівнюються нове значення критерія Р, і старе значення РС, одержане на попередньому крокові.
Якщо потужність ХДС зросла (РРС), то крок зроблено у вірному напрямку і потрібно рух продовжити, нічого не змінюючи в процедурі пошуку.
Якщо ж значення критерія Р зменшилось, це означає, що на цьому кроці був перейдений максимум, і потрібно повернути назад. Одночасно потрібно зменшити розмір кроку, бо інакше процедура буде зациклена на повторюванні двох значень Р – зліва та справа від максимуму. Оператор if Р>РC then goto 1, виявивши, що логічна умова РРС не виконується, не виконує і посилання на помітку 1 , тому виконується наступний за ним оператор дії пошукового алгоритму dI:= – dI*0.4: змінюється напрямок руху по осі струму (dI= – dI ) і зменшується величина (*0.4) кроку . Коефіцієнт зменшення кроку 0.4 тут обраний довільно, від його значення залежить не кінцевий результат пошуку, а лише кількість кроків.
На кожному кроці в кінці всіх операцій потрібно запам’ятати нове значення критерія Р як минуле значення РС оператором РС=Р. Значення РС буде використано на наступному крокові для порівняння з відповідним наступним значенням Р.
Пошук закінчується, коли крок зменшиться до заданого значення помилки eps .
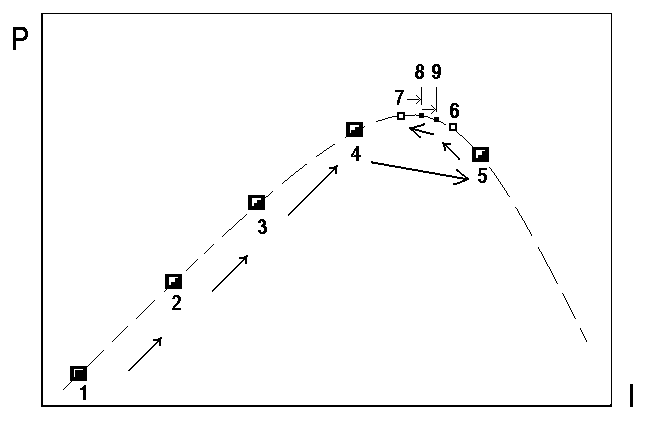
Рис. 2.3.4. Схема
пошуку максимуму функції
![]() .
Цифрами позначені порядкові номери
точок в процесі пошуку, стрілками –
напрям руху.
.
Цифрами позначені порядкові номери
точок в процесі пошуку, стрілками –
напрям руху.
LABEL 1,2;
