
- •Мазмұны
- •1.2 Жалпы түсініктер
- •1.2 Қалдықпен бөлу
- •1.3 Ең үлкен ортақ бөлгіш және ең кіші ортақ еселік
- •Мунда жазу керек
- •1.4 Сандар теорясының негізгі теоремасы
- •2. Бөлінгіштікке қатысты қалыпты емес есептер
- •2.1 Математикалық индукция әдісі. Ньютон биномының формуласы.
- •2.2 Бөлінгіштік белгілері
- •2.3 Көбейткіштерге жіктеу формулаларын қолдану
- •2.4 Қалдықпен бөлу
- •2.5 Өзара жай сандар
1.2 Жалпы түсініктер
Сандар
теориясының негізгі объектісі ретінде
1,2,3,...., натурал сандары, 0 саны және барлық
теріс -1,-2,-3,..., сандары алынады. Бұл
сандардың барлығы бүтін сандардың
жиынын құрайды. Бүтін сандар жиынын
 деп белгілейді. Яғни,
деп белгілейді. Яғни,

Мұндағы,
 -бүтін
оң сандар,
-бүтін
оң сандар,
 - бүтін теріс сандар.
- бүтін теріс сандар.
Бүтін сандар жиынының екі не одан да көп элементтеріне қосу, азайту және көбейту амалдарын қолданғанда шығатын элемент те сол жиынның элементі болады. Осы үш амалға қатысты алғанда тұйық болатын, яғни амал қолданғандағы шыққан элемент те сол жиынында жататын, сандар жиынын сақина деп атау қабылданған. Бұдан былайғы жерде өзіміз қарастыратын сақинаны бүтін сандар сақинасы деп атайтын боламыз. Бүтін сандарды қосу, азайту көбейту амалдары, бүтін санның модулі және оның қасиеттері белгілі деп есептеп, бүтін сандар сақинасының элементтерінің бөлінгіштік қасиеттерін қарастырамыз.
1-анықтама.
Бүтін
 және
және сандары үшін
сандары үшін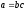 болатын бүтінс
саны
табылса, онда а
саны
болатын бүтінс
саны
табылса, онда а
саны
 -ға
бөлінеді деп атайды.
-ға
бөлінеді деп атайды.
Егер
 саны
саны -ға
бөлінсе, она
-ға
бөлінсе, она арқылы
белгілейді.
арқылы
белгілейді.
Бүтін
сандар жиыны
 -те
бұл қатынас төмендегі қасиеттерді
қанағаттандырады:
-те
бұл қатынас төмендегі қасиеттерді
қанағаттандырады:
Бөлінгіштік қатынасы рефлексивтік, яғни кез келген
 үшін
үшін .
.Бөлінгіштік қатынасы транзитивті, яғни
 және
және болса,
онда
болса,
онда .
.
3. Егер
 болса, онда
болса, онда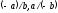 және
және яғни бөлінгіштік қатынасы бөлінгіш пен
бөлгіштің таңбаларын ауыстырғанда да
сақталады.
яғни бөлінгіштік қатынасы бөлінгіш пен
бөлгіштің таңбаларын ауыстырғанда да
сақталады.
4. Егер
 және
және болса, онда
болса, онда
5. Егер
 және
және
 ,
болса онда
,
болса онда
 .
.
6. Егер
 және
және болса, онда
болса, онда ,
мұндағы,
,
мұндағы, және
және кез келген бүтін сандар.
кез келген бүтін сандар.
7. Егер
 болып, ал
болып, ал саны
саны -ға
бөлінбесе, онда
-ға
бөлінбесе, онда саны да с-ға бөлінбейді.
саны да с-ға бөлінбейді.
8. Ноль
саны кез келген а
санына
бөлінеді. Себебі,

9. Кез
келген сан 1 санына бөлінеді. Себебі,
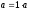
10. Егер
а:b
болса, онда
 .
.
11. Егер
 және
және болса, онда
болса, онда не
не

Ескерту. 4 және 5 тұжырымға кері тұжырым дұрыс емес: бірнеше
санның қосындысының бөлінгіштігінен, қосылғыштар бөлінгіштігі, ал көбейтіндінің бөлінгіштігінен көбейткіштердің бөлінгіштігі шықпайды.
Мысалы,
 саны 8-ге бөлінеді, бірақ 27-де, 13-те 8-ге
бөлінбейді.
саны 8-ге бөлінеді, бірақ 27-де, 13-те 8-ге
бөлінбейді.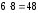 саны 12-ге бөлінеді, бірақ не 6, не 8 саны
12-ге бөлінбейді.
саны 12-ге бөлінеді, бірақ не 6, не 8 саны
12-ге бөлінбейді.
1.2 Қалдықпен бөлу
2-анықтама. Егер q және r бүтін сандары табылып

 (1)
(1)
теңдігі орындалса, онда а саны b-ға қалдықпен бөлінеді деп аталады. Мұндағы q-бөлінді, ал r-қалдық деп аталады.
1-теорема.
Кез келген бүтін
 саны
саны бүтін санына қалдықпен бөлінеді және
бұл бөлу жалғыз түрде өрнектеледі.
бүтін санына қалдықпен бөлінеді және
бұл бөлу жалғыз түрде өрнектеледі.
Дәлелдеуі. Әуелі қалдықпен бөлудің бар екенін дәлелдейік. Ол үшін екі жағдайды қарастырамыз.
 кез
келген бүтін сан, ал
кез
келген бүтін сан, ал
 болсын.
болсын.
 -ға
еселі барлық бүтін сандарды, өсу ретімен
орналастырып, қарастырайық:
-ға
еселі барлық бүтін сандарды, өсу ретімен
орналастырып, қарастырайық:

 санының
санының -дан
аспайтын ең үлкен еселігі
-дан
аспайтын ең үлкен еселігі болсын. Онда
болсын. Онда демек
демек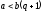 яғни
яғни Теңсіздіктің барлық жағынан
Теңсіздіктің барлық жағынан -ді
шегерсек
-ді
шегерсек теңсіздігін аламыз.
теңсіздігін аламыз. деп белгілесек, онда келесі теңдікті
аламыз:
деп белгілесек, онда келесі теңдікті
аламыз: .
.
 -бүтін,
ал
-бүтін,
ал
 болсын.
болсын.
 болғандықтан
болғандықтан
 ,
онда 1-ші жағдай бойынша а саны –
,
онда 1-ші жағдай бойынша а саны – санына қалдықпен бөлінеді, демек бүтін
q және r сандары табылып
санына қалдықпен бөлінеді, демек бүтін
q және r сандары табылып
 немесе
немесе орындалады. Кез келген бүтін а және
орындалады. Кез келген бүтін а және сандары үшін (1) теңдіктің орындалатынын
дәлелдедік.
сандары үшін (1) теңдіктің орындалатынын
дәлелдедік.
Енді қалдықпен бөлудің, яғни (1) теңдіктің, жалғыз түрде анықталатынын дәлелдейік.
 санын
санын
 -ға
бөлгендегі анықталатын (1) өрнек жалғыз
емес дейік. Яғни
-ға
бөлгендегі анықталатын (1) өрнек жалғыз
емес дейік. Яғни және
және сандары табылып, төмендегі теңдіктер
орындалады:
сандары табылып, төмендегі теңдіктер
орындалады:
 және
және
 Бұл теңдіктерден
Бұл теңдіктерден немесе
немесе шығады.
шығады.
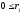 және
және
 теңсіздіктерінен,
теңсіздіктерінен, ,
ал
,
ал және
және теңсіздіктерінен,
теңсіздіктерінен, теңсіздіктерін аламыз. Яғни,
теңсіздіктерін аламыз. Яғни, ,
бұдан
,
бұдан .
Егер
.
Егер десек, онда
десек, онда және
және .
Бұндай теңсіздік мүмкін емес. Ендеше
.
Бұндай теңсіздік мүмкін емес. Ендеше ал
ал болғандықтан
болғандықтан
Демек,
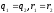 болғандықтан (1) түрдегі өрнек жалғыз.
болғандықтан (1) түрдегі өрнек жалғыз.
