4.Общее уравнение прямой

Уравнение

Ах+Ву+С=0

(где А, В, С могут иметь любые значения, лишь бы коэффициенты А, В не были нулями оба сразу) представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.

Если А=0, то есть уравнение не содержит х, то оно представляет прямую, параллельную оси ОХ.

Если В=0, то есть уравнение не содержит у, то оно представляет прямую, параллельную оси ОY.

Когла В не равно нулю, то общее уравнение прямой можно разрешить относительно ординаты у, тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при А отличным от нуля общее уравнение прямой можно разрешить относительно х.

Если С=0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат

5.  

Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

y - y₁ = k(x - x₁).     (1)

Это уравнение определяет пучок прямых, проходящих через точку A(x₁, y₁), которая называется центром пучка.

6

. Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

     (2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

     (3)

7Уравнение прямой в отрезках

Если в общем уравнении прямой  , то разделив (1) на  , получаем уравнение прямой в отрезках

 ,

 

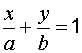где 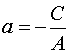 ,  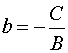. Прямая пересекает ось   в точке  , ось   в точке  .

8Формула: Угол между прямыми на плоскости

У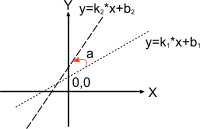голα между двумя прямыми, заданными уравнениями: y=k₁x+b₁ (первая прямая) и y=k₂x+b₂ (вторая прямая), может быть вычислен по формуле (угол отсчитывается от 1^й прямой ко 2^й против часовой стрелки):

tg(α)=(k₂-k₁)/(1+k₁k₂)

9 Взаимное расположение двух прямых на плоскости.

  Пусть сейчас оба уравнения прямых записаны в общем виде.

Теорема. Пусть

    и 

– общие уравнения двух прямых на координатной плоскости Оху. Тогда

1) если , то прямые  и  совпадают;

2) если , то прямые   и 

    параллельные;

3) если , то прямые пересекаются.

   Доказательство. Условие  равносильно коллинеарности нормальных векторов данных прямых:

. Поэтому, если , то  и прямыепересекаются.

   Если же , то , ,  иуравнение прямой  принимает вид:

 или , т.е. прямые совпадают. Заметим, что коэффициент пропорциональности , иначе все коэффициенты общего уравнения были бы равны нулю, что невозможно.

   Если же прямые не совпадают и не пересекаются, то остается случай , т.е. прямые параллельны.

Теорема доказана.

10

Для определения расстояния от точки до прямой необходимо знать уравнения прямой и координаты точки в декартовой системе координат. Расстоянием от точки до прямой будет являться перпендикуляр, проведенный из этой точки к прямой.

Инструкция

1

Общее уравнение прямой в декартовых координатах имеет вид Ax+By+C=0, где A, B и C - известные числа. Пусть точка O имеет координаты (x1, y1) в декартовой системе координат.

В этом случае отклонение этой точки от прямой равно δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)), если C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

Расстояние от точки до прямой - это модуль отклонения точки от прямой, то есть r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))|, если C<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

2

Пусть теперь точка с координатами (x1, y1, z1) задана в трехмерном пространстве. Прямая может быть задана параметрически, системой из трех уравнений: x = x0+ta, y = y0+tb, z = z0+tc, где t - действительное число. Расстояние от точки до прямой можно найти как минимальное от этой точки до произвольной точки прямой. Коэффициент t этой точки равен tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2))

3

Расстояние от точки (x1, y1) до прямой можно посчитать и в случае, если прямая задана уравнением с угловым коэффициентом: y = kx+b. Тогда уравнение перпендикулярной ей прямой будет иметь вид: y = (-1/k)x+a. Далее нужно учесть, что эта прямая должна проходить через точку (x1, y1). Отсюда находится число a. После преобразований находится и расстояние между точкой и прямой.

31 . Базис на плоскости и в пространстве

Определение. Базисом на плоскости называются два любых линейно независимых вектора.

два любых неколлинеарных вектора образуют базис. Пусть a любой вектор на плоскости, а векторы  b и c образуют базис. Так как на плоскости всякие три вектора линейно зависимы, то вектор a линейно выражается через векторы базиса, т. е. выполняется соотношение

Определение. Базисом в пространстве называются три любых линейно независимых вектора. три любых некомпланарных вектора образуют базис. Как и в случае плоскости, устанавливается, что любой вектор a разлагается по векторам b, c и d

Общее определение (чтобы понятно всем было) Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов. Любой вектор однозначным образом раскладывается по базису. Коэффициенты разложения называются координатами этого вектора относительно данного базиса. Векторы образуют базис в декартовом координатном пространстве Oxyz.