Делать лабораторные работы 3,4

Продолжение таблицы 4.1

2x + x +4x =9

−2x − x + x =1

1

3

4

2

3

4

x1

+2x2 − x3 + x4 =8

−6x1 +3x3 − x4 = 0

a) 7x

− x

2

+ x

+ x

=5

a) 2x

+ x

− x − x

= −6

1

3

4

1

2

3

4

14

x − x

+3x

+ x

= −2

29

2x

+1x

− x

= 2

1

2

3

4

2

3

4

x −2y +3z =5

4x −3y − z = −4

+3y −4z =12

b) 2x

b) 2x +5y +3z = 2

−2y −5z =15

3x

−3y +2z = 2

2x1 −6x2 +2x3 +2x4 =12

5x1 +7x2 +2x3 + x4 = 4

x +3x +5x +3x = 6

−x

−4x

− x

−

2x

= 0

a)

1

2

3

4

a)

1

2

3

4

2x

+3x

−3x

− x

=3

2x1 −2x2 +7x3 = 0

−7x2 + x3 − x4 = −4

1

2

3

4

15

5x1

30

2x

+3x

− x

=1

3x +4y +2z =8

1

3

4

−3x −2y + z = 5

− y −3z = −1

−2z =15

b) 2x

b) −y

+5y + z = 0

−x

3x −6y +2z = −3

Порядок выполнения задания

При выполнении лабораторной работы систему линейных алгебраических уравнений необходимо решать методом обратной матрицы и методом Крамера. Вспомним основные формулы, используемые в этих методах.

Метод обратной матрицы.

Систему линейных алгебраических уравнений AX = b умножим слева на матрицу, обратную к А. Система уравнений примет вид:

A-1AX=A-1b, EX=A-1b, (E - единичная матрица).

Таким образом, вектор неизвестных вычисляется по формуле X=A-1b.

Метод Крамера.

В этом случае неизвестные x1,x2,…, xn вычисляются по формуле: xi = ∆∆i ,i =1,..., n ,

где ∆– определитель матрицы A;

∆i –определитель матрицы, получаемой из матрицы А путем заме-

ны i-го столбца вектором b.

Обратите внимание на особенность работы с матричными формулами: необходимо предварительно выделять область, в которой будет храниться результат, а после получения результата преобразовывать его к матричному ви-

ду, нажав клавиши F2 и Ctrl+Shift+Enter.

Теперь рассмотрим решение системы линейных уравнений методом обратной матрицы и методом Крамера на конкретных примерах. Решим сле-

52

дующую систему линейных алгебраических уравнений методом обратной матрицы:

x2 −13x3 +4x4 = −5;x1 −2x3 +3x4 = −4;

3x1 +21x2 −5x4 = 2;

4x1 +3x2 −5x3 =3.

В этом случае матрица коэффициентов А и вектор свободных коэффициентов b имеют вид:

0		1	−13 4					−5
	1	0	−2	3				−4
A =						,	b =
	3	21	0	−5				2	.
	4	3	−5	0				3

Введём матрицу A и вектор b в рабочий лист MS Excel (рис. 4.1).

Рис. 4.1. Ввод матрицы A и вектора b

В нашем случае матрица А находится в ячейках B1:Е4, а вектор b в диапазоне G1:G4. Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы (это нужно сделать обязательно!!!); пусть в нашем случае это будут ячейки B6:E9. Теперь обратимся к мастеру функций, и в категории «Математические» выберем функцию МОБР, предназначенную для вычисления обратной матрицы (рис. 4.2), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций. В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода «Массив» (рис. 4.3). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:E4. Данные в поле ввода «Массив» можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.

53

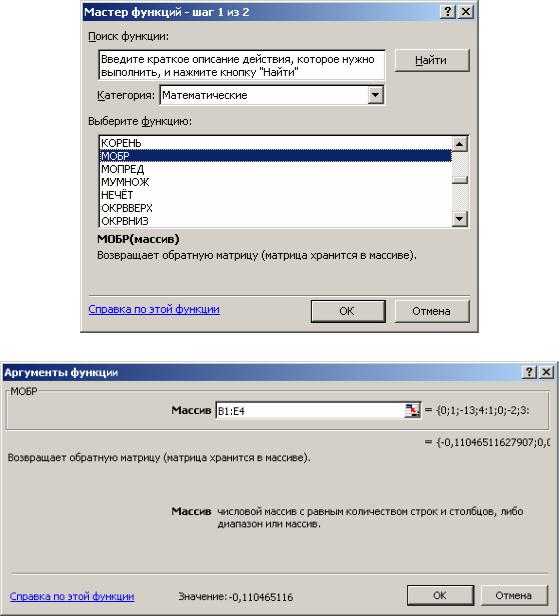
Рис. 4.2. Мастер функций

Рис. 4.3. Нахождение обратной матрицы

Если поле «Массив» заполнено, можно нажать кнопку OK. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид, изображенный на рис. 4.4.

54

Рис. 4.4. Фрагмент рабочего листа с полученной обратной матрицей Aобр

Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например H6:H9. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ≠ВА

Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 4.5) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B6:E9 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G1:G4 (вектор b)

Рис. 4.5. Перемножение обратной матрицы Aобр и вектора В

Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу

55

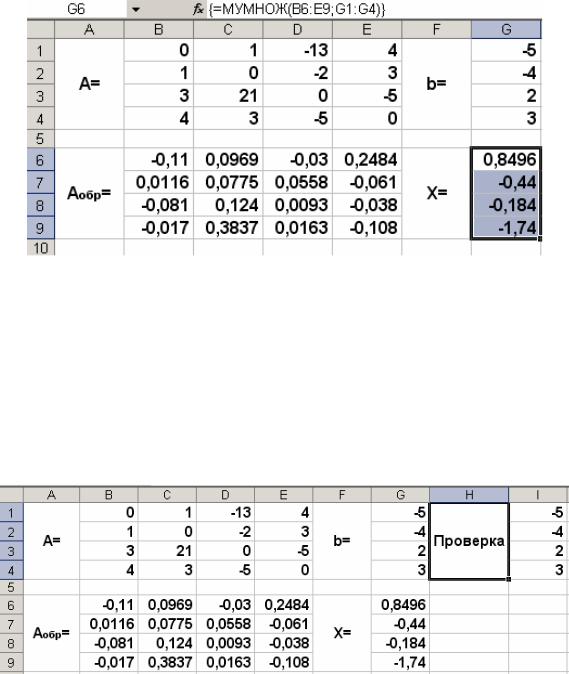
F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений (вектор X), находится в ячейках G6:G9 (рис. 4.6).

Рис. 4.6. Фрагмент рабочего листа с найденным вектором X

Таким образом, мы решили систему линейных алгебраических уравнений методом обратной матрицы. Корни: X1, X2, X3, X4 будут, в нашем случае, соответствовать ячейкам G6, G7, G8 и G9.

Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор Х и получить в результате вектор b. Умножение матрицы A на вектор Х осуществляется при помощи функции МУМНОЖ(В1:Е4;G6:G9) так, как было описано выше.

В результате проведенных вычислений рабочий лист примет вид, изображенный на рис. 4.7.

Рис. 4.7. Фрагмент рабочего листа с результатом проверки решения

Теперь рассмотрим пример решения этой же системы линейных алгебраических уравнений методом Крамера. Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 4.8)

56

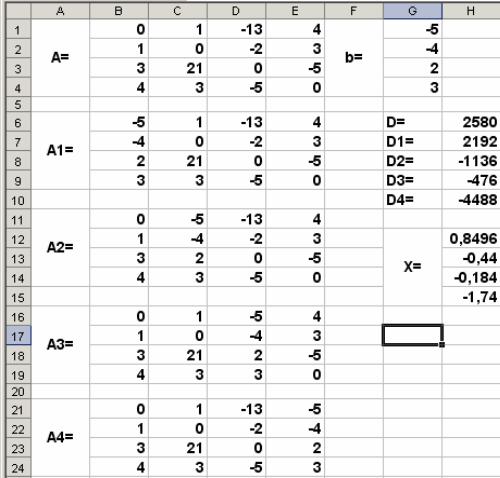
Рис. 4.8. Фрагмент рабочего листа с результатом решения системы методом Крамера

Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку H6 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге, содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B1:E4.

Для вычисления вспомогательных определителей введем формулы:

H7=МОПРЕД(B6:E9),

H8=МОПРЕД(B11:E14),

H9=МОПРЕД(B16:E19),

H10=МОПРЕД(B21:E24).

В результате в ячейке H6 хранится главный определитель, а в ячейках H7:H10 – вспомогательные.

Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку H12 введём формулу =H7/$H$6. Затем скопируем её содержимое в ячейки H13, H14 и H15. Система решена.

57

ЛАБОРАТОРНАЯ РАБОТА № 5

Решение нелинейных уравнений и систем

Цель работы: Приобретение навыков решения нелинейных уравнений и систем средствами пакета.

Задание 1. Найти корни полинома (на первом листе рабочей книги)

Таблица 5.1

Варианты задания 1

	№		Уравнение	№	Уравнение
	1	a)x4	−18 x2 +6 = 0;	16	a)3 x4 +4 x3 −12 x2 −5 = 0;
		b)x3	+0,1 x2 +0, 4 x −1, 2 = 0.		b)x3	−3 x2 +9 x +2 = 0.
	2	a)2 x4 − x2 −10 = 0;		17	a)2 x3 −9 x2 −60 x +1 = 0;
		b)x3	+0, 2 x2 +0,5 x −2 = 0.		b)x3	+2 x2 +4 = 0.
	3	a)3 x4 +4 x3 −12 x2 +1 = 0;		18	a)3 x4 +4 x3 −12 x2 −5 = 0;
		b)x3	+0,1 x2 +0,3 x −0,6 = 0.		b)x3	−0,1 x2 +0, 4 x −1,5 = 0.
	4	a)3 x4 +8 x3 +10 = 0;		19	a)3 x4 −8 x3 −18 x2 +2 = 0;
		b)x3	+0, 2 x2 +0,5 x −1, 2 = 0.		b)x3	+0,1 x2 +0, 4 x −1, 2 = 0.
	5	a)3 x3 +9 x2 −60 x +1 = 0;		20	a)x4	− x −1 = 0;
		b)x3	−3 x2 +6 x +3 = 0.		b)x3	−0, 2 x2 +0,3 x −1, 2 = 0.
	6	a)2 x4 −8 x3 +8 x2 −1 = 0;		21	a)x4	−4 x3 −8 x2 +1 = 0;
		b)x3	−3 x2 +12 x −12 = 0.		b)x3	+3 x +1 = 0.
	7	a)x4	− x3 −2 x2 +3 x −3 = 0;	22	a)2 x4 −8 x3 +8 x2 −1 = 0;
		b)x3	+4 x −6 = 0.		b)x3	−3 x2 +12 x −9 = 0.
	8	a)3 x4 −8 x3 −18 x2 +2 = 0;		23	a)2 x4 − x2 −10 = 0;
		b)x3	−3 x2 +6 x −2 = 0.		b)x3	−0, 2 x2 +0,5 x −1 = 0.
	9	a)3 x4 +4 x3 −12 x2 +1 = 0;		24	a)x4	−18 x2 +6 = 0;
		b)x3	+0, 2 x2 +0,5 x +0,8 = 0.		b)x3	−0,1 x2 +0, 4 x +2 = 0.
	10	a)3 x4 +4 x3 −12 x2 +1 = 0;		25	a)x4	− x3 −2 x2 +3 x −3 = 0;
		b)x3	+3 x2 +6 x −1 = 0.		b)x3	−3 x2 +6 x −5 = 0.
	11	a)x4	−18 x2 +6 = 0;	26	a)3 x4 +8 x3 +6 x2 −10 = 0;
		b)x3	−0,1 x2 +0, 4 x +1, 2 = 0.		b)x3	+0, 4 x2 +0,6 x −1,6 = 0.
	12	a)3 x4 +8 x3 +6 x2 −10 = 0;		27	a)x4	+4 x3 −8 x2 −17 = 0;
		b)x3	+3 x2 +12 x +3 = 0.		b)x3	−0, 2 x2 +0,5 x −1, 4 = 0.

58

					Продолжение таблицы 5.1
13	a)x4	+4 x3 +8 x2 −17 = 0;	28	a)3 x4 +4 x3 −12 x2 −5 = 0;
	b)x3	+3 x −1 = 0.		b)x3	+2 x2 +2 = 0.
14	a)2 x4 − x2 −10 = 0;		29	a)2 x4 −9 x2 −60 x +1 = 0;
	b)x3	−0, 2 x2 +0, 4 x −1, 4 = 0.		b)x3	−2 x +2 = 0.
15	a)x4	− x −1 = 0;	30	a)x4	− x −1 = 0;
	b)x3	−3 x2 +9 x −10 = 0.		b)x3	+ x −3 = 0.

Порядок выполнения задания 1

Найдем корни полинома x3 - 0,01x2 - 0,7044x + 0,139104 = 0. Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.

Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на рис. 5.1., где в ячейку В2 бы-

ла введена формула: = A2^3 - 0,01*A2^2 - 0,7044*A2 + 0,139104.

На графике видно, что функция три раза пересекает ось X, а так как полином третьей степени имеется не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].

Затем необходимо ввести приблизительное значение корней, найденных графически в ячейки A16, A17 и A18 соответственно и скопировать формулу в ячейки В16, В17 и В18 (в данном конкретном случае) как показано на рис. 5.1.

59

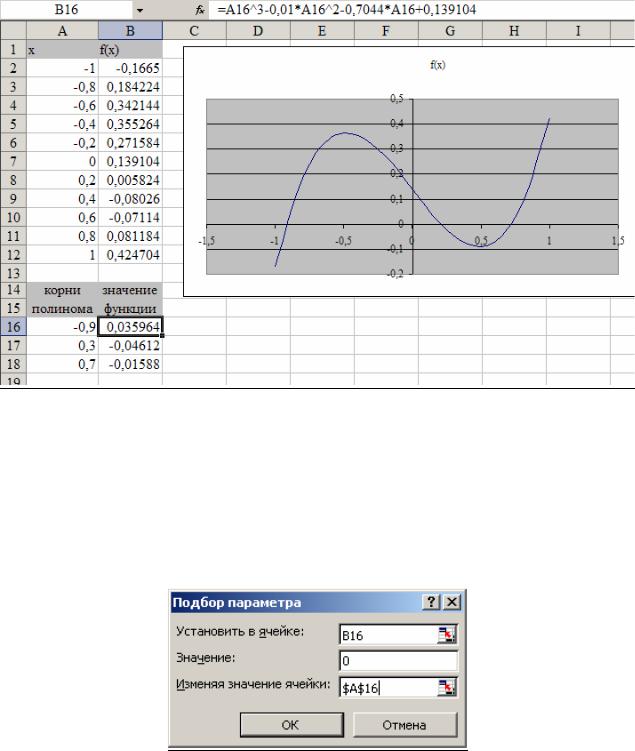
Рис. 5.1. Нахождение корней полинома графически

Теперь можно найти корни полинома методом последовательных приближений с помощью команды Сервис → Подбор параметра. Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис → Параметры. После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис → Подбор параметра и заполнить диалоговое окно следующим образом (см.

рис. 5.2).

Рис. 5.2. Уточнение значений корней полинома

В поле Установить в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (уравнение должно быть записано так, чтобы его правая часть не содержала переменную). В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля диалогового окна Подбор параметров удоб-

60

нее не с клавиатуры, а щелчком на соответствующей ячейке.

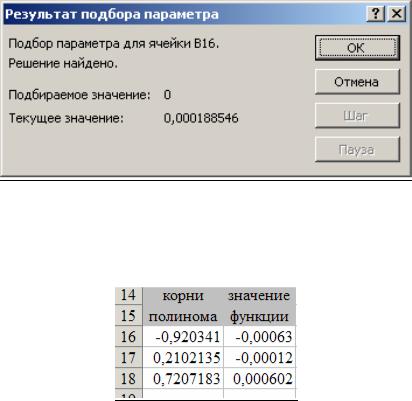
После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (см. рис.5.3) с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А16.

Рис. 5.3. Уточнение значений корней полинома

Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А17 и А18 (см. рис. 5.4)

Рис. 5.4. Значений корней полинома

В итоге получаем корни нелинейного уравнения X1, X2 и X3, значения которых находятся в ячейках А16, А17 и А18 соответственно.

61