3-Б курс, 6-ти летки Калинина Т.В 2 / МУ для выполнения КР ЭиЭ

Окончание табл. 3.1

1

2

3

Действующее

значе-

I

R

i

R

ние переменного тока

А

А

–

сила

постоянного

E

e

тока, который проте-

кая

через

равное

со-

Rр

Rр

противление и за одно

и то же время, что и

переменный ток, вы-

деляет одинаковое ко-

личество теплоты

Начальная

фаза

–

Например, ток в цепи

электрический угол ψ,

описывается следующим

характеризующий зна-

выражением

чение ЭДС, тока или

i=100sin(ωt+30°),

напряжения

в

началь-

тогда начальная фаза то-

ный момент времени

ка ψi=30°.

Или i=100sin(ωt ),

тогда ψi= .

а)

б)

e

Em sin(

t

e )

а)

б)

e

Em sin(

t

e )

Угол сдвига фаз φ

1

2

или φ=ψU ψI

разность

начальных

Например, ток и напря-

фаз двух синусоидаль-

жение в цепи описывают-

ных величин одной и

ся выражениями

той же частоты

i=100sin(ωt+30°) и

u=150sin(ωt+60°).

Напряжение опережает

ток по фазе, тогда

φ=ψU ψI=60°-30°=30°.

Синусоидальные величины могут быть представлены следующими способами: тригонометрическими функциями (u=Umsinωt), временными диаграммами или графиками изменения функции во времени (рис. 3.1, а), вращающимися векторами (рис. 3.1, б), комплексными числами.

		y
		Im	ωt1
i1	i0		Im
			Ψ
			x
		α=Ψ+ωt1
а)			б)
Рис. 3.1
30

Вектора можно складывать и вычитать (табл. 3.2).
	Таблица 3.2
Действие	Графические действия
Сложение
векторов ЭДС,
совпадающих по
фазе
Сложение
векторов
методом
переноса
Вычитание
векторов
3.1. Расчет линейной электрической цепи однофазного синусоидального
	тока символическим методом

Рассмотрим более подробно символический метод расчета линейных электрических цепей синусоидального тока, основанный на использовании комплексных чисел, который получил широкое применение.

Для определения в произвольный момент времени t значения переменного тока i заданной частоты ω необходимо знать два числа, амплитуду Im и начальную фазу ψ. Тогда в любой момент времени можно записать

Однако вместо двух действительных чисел можно пользоваться одним комплексным числом.

Комплексное число А состоит из вещественной A’ и мнимой A” частей А= A’+jA”. Комплексное число на комплексно-числовой плоскости можно представить вектором. Проекция вектора на вещественную ось (ось абсцисс) соответствует вещественной части комплексного числа A’. Проекция вектора на мнимую ось j (ось ординат) соответствует мнимой части комплексного числа A” (рис. 2.2), j мнимая единица, представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки (т.е. в положительном направлении).

31

Рис. 3.2. Графическое изображение комплексного числа на комплексно-числовой плоскости

Например, на рис. 3.3 изображены векторы комплексных чисел А=2+j4 и

B=3 j2.

Рис. 3.3

Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число. Из построения (рис. 3.3) видно, что модуль комплексного числа:

.

Тогда модуль числа А=2+j4

,

а модуль числа B=3 j2

,

Углы φА и φВ, образованные векторами А и В и положительным направлением вещественной оси, называют аргументами комплексного числа. Аргумент комплексного числа определяется выражением:

Тогда для приведенных примеров

C помощью вышеприведенных вычислений получаем показательную

форму комплексного числа:
,	.
	32

Аргумент комплексного числа В отрицательный, т.к. вектор повернут на угол φВ по часовой стрелке.

Существует три записи комплексного числа:
1.	Алгебраическая А= A’+jA”: А=2+j4 и B=3 j2.
2.	Тригонометрическая	, т.к.

и

3. Показательная

, откуда следует, что по-

воротный множитель (формула Эйлера)

Рассмотрим несколько характерных примеров вычислений с поворотным множителем, результаты которых полезно запомнить:

Тогда для приведенных примеров:

, .

Показательную форму можно перевести в алгебраическую, и наоборот. Например,

Действия над комплексными числами

Комплексные числа можно складывать, вычитать, умножать и делить.

Сложение и вычитание комплексных чисел производится только в ал-

гебраической форме! Умножение и деление комплексных чисел можно про-

изводить как в алгебраической, так и в показательной форме. Однако ум-

ножение и деление комплексных чисел удобно производить в показательной форме. При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:

.

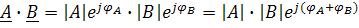При делении комплексных чисел в показательной форме модули чисел делятся, а аргументы вычитаются:

33

Для совершения данных вычислительных действий необходимо вспомнить следующие правила действий с мнимой частью комплексного числа, результа-

ты которых полезно запомнить!

Кроме того, единичный множитель можно записать равенством:

j e	j90
	.

Тогда для приведенных примеров действия в алгебраической форме:

Однако умножение и деление комплексных чисел удобно производить в показательной форме. При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:

.

При делении комплексных чисел в показательной форме модули чисел делятся, а аргументы вычитаются:

Таким образом, сложение и вычитание комплексных чисел можно производить только в алгебраической форме, а умножение и деление удобней и проще производить в показательной форме.

Комплексы тока и напряжения

Если ток и напряжение изменяются по синусоидальному закону и , то как указывалось выше, их можно изобразить векторами и, следовательно, записать в комплексном виде:

, ,

где комплексы тока и напряжения (отсутствие индекса m означает, что записано действующее значение комплексной величины). Точка над комплек-

34

сом означает, что ток и напряжение изменяются по синусоидальному закону с определенной частотой ω;

I и U – модули комплексов тока и напряжения, они же действующие значения тока и напряжения ;

и – аргументы комплексов тока и напряжения, они же начальные фазы тока и напряжения и

Комплекс сопротивления и проводимости

Комплекс полного сопротивления цепи Z определяется отношением комплекса напряжения на выводах цепи (ветви) к комплексу тока (комплексы вели-

чин, не зависящих от времени, обозначаются большими буквами с черточкой внизу), т.е.

или
где	– модуль комплексного сопротивления;

φ – аргумент комплекса полного сопротивления или угол сдвига фаз между током и напряжением φ;

R=cosZ – активное сопротивление цепи или вещественная часть комплекса полного сопротивления;

X=sinZ – реактивное сопротивление цепи или мнимая часть комплекса полного сопротивления (коэффициент перед мнимой единицей). Знак перед мнимой единицей j указывает на характер цепи (знак «+» в цепи преобладает индуктивная нагрузка, знак « » в цепи преобладает емкостная нагрузка).

Обратная величина комплекса проводимости

где – модуль комплексного сопротивления;

φ – аргумент комплекса полной проводимости или угол сдвига фаз между током и напряжением φ;

B=cosY – активная проводимость цепи или вещественная часть комплекса полной проводимости;

G=sinY – реактивная проводимость цепи или мнимая часть комплекса пол-

ной проводимости. Знак перед мнимой единицей j указывает на характер цепи (знак « » в цепи преобладает индуктивная нагрузка, знак «+» в цепи преобладает емкостная нагрузка).

Комплекс мощности

Произведение комплекса напряжения и сопряженного комплекса тока представляет полную мощность в комплексной форме или комплексную мощность.

35

Комплексные величины, имеющие одинаковые модули равные по абсолютному значению, но противоположные по знаку аргументы, называются со-

пряженными. Сопряженный комплекс отмечается звездочкой, но мы его бу-

дем отмечать галочкой из-за возможностей редактора формул программы

Microsoft Word 2007. Например, для комплекса сопряженным будет:

.

Как видно из вышеприведенной формулы у сопряженного числа изменяется знак перед мнимой частью и перед аргументом.

Тогда

где	– модуль комплексной мощности;

φ – аргумент комплекса полной мощности или угол сдвига фаз между током и напряжением φ;

P=cosS – активная мощность цепи или вещественная часть комплекса полной мощности;

Q=sinS – реактивная мощность цепи или мнимая часть комплекса полной мощности. При емкостной нагрузке, т.е. при φ<0, мнимая часть комплексной мощности имеет отрицательный знак; при индуктивной нагрузке, т.е. при φ>0, мнимая часть комплексной мощности имеет положительный знак.

Выражения комплексов сопротивлений, проводимостей, мощностей, векторные диаграммы токов и напряжений приведены в прил. 1.

Закон Ома и законы Кирхгофа в комплексной форме

Любую цепь переменного тока можно рассчитать по законам постоянного тока (Ома, Кирхгофа), если все величины представить в комплексной форме. Как и в цепях постоянного тока, для записи уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов и обходов контуров.

Тогда

закон Ома в комплексной форме

первый закон Кирхгофа в комплексной форме – алгебраическая сумма комплексных токов в узле равна нулю

второй закон Кирхгофа в комплексной форме – для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна сумме комплексных падений напряжений

36

3.2.Пример решения задачи № 2

Всоответствии с исходными данными (табл. 3.3) выполнить расчет линейной электрической цепи однофазного синусоидального тока со смешанным со-

единением активных и реактивных элементов символическим методом (рис. 3.4), а именно:

1)составить схему замещения электрической цепи;

2)определить напряжения на всех участках цепи и на отдельных элементах, токи во всех ветвях схемы;

3)проверить правильность определения токов, используя первый закон Кирхгофа;

4)рассчитать полную мощность всей цепи и на отдельных ее участках;

5)составить баланс активных и реактивных мощностей;

6)построить в масштабе векторную диаграмму токов и напряжений в цепи.

Z1

1

2

U

13

Z2

Z3

Z4

3

3

Рис. 3.4. Расчетная схема

Таблица 3.3

U14,

Ψu,

f,

R1,

L1,

С1,

R2,

L2,

С2,

R3,

L3,

С3,

B

град.

Гц

Ом

мГн

мкФ

Ом

мГн

мкФ

Ом

мГн

мкФ

100

15

50

5

2

400

3

10

Решение.

1.Составляем схему замещения электрической цепи в соответствии с исходными данными (рис. 3.5):

1

XL1

2

S2

S3

I1

S1

R2

R3

U14

I2

I3

XC2

XL3

3

3

Рис. 3.5

37

2.Рассчитываем индуктивные и емкостные сопротивления цепи:

3.Записываем полные сопротивления всех участков цепи в алгебраической

ипоказательной формах:

Для записи показательной формы комплексного сопротивления 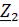определяем его модуль

и аргумент комплексного сопротивления:

Для записи показательной формы комплексного сопротивления определяем его модуль

и аргумент комплексного сопротивления:

4. Определяем ток I1 в неразветвленной части цепи.

Так как цепь представляет собой смешанное соединение приемников (см. рис. 3.3), то для нахождения тока в неразветвленной части цепи схему необходимо упростить до общего сопротивления .

4.1. Эквивалентируем сопротивления Z2 и Z3, соединенные параллельно:

Для того, чтобы в вышеприведенной формуле поделить числитель на знаменатель, находим модуль комплексного числа в знаменателе и его аргумент.

Так как следующим действием упрощения схемы будет сложение трех последовательно соединенным сопротивлений цепи необходимо перевести показательную форму сопротивления в алгебраическую форму через тригонометрическую:

4.2. Определяем общее сопротивление цепи .

38

В результате эквивалентного преобразования сопротивлений Z2 и Z3 получаем следующую схему (рис. 3.6, а):

1			Z1			2
									1			Zобщ		3
			I1					Z23
												I1
3
					а							б

Рис. 3.6

Теперь сопротивления Z1 и Z23 соединены последовательно, следовательно, находим общее сопротивление цепи (рис. 3.6, б) как их сумму.

4.3. Определяем ток в неразветвленной части цепи по закону Ома:

5.Определяем напряжения на всех участках цепи.

6.Определяем токи во всех ветвях схемы.

7.Проверяем правильность определения токов по первому закону Кирхгофа, составив уравнение для узла 2:

Проверка по первому закону Кирхгофа сходится, значит, токи определены верно.

8. Рассчитываем напряжения на отдельных элементах схемы (см. рис. 3.5):

9. Определяем полную мощность всей цепи, мощности на всех участках схемы:

39