Плотность распределения Стьюдента – чётная функция

p(T t) p(T t)

Критическая точка tпр,кр находится из требования:

p(T tпр,кр )

p(T tпр,кр )

–tпр,кр является критической точкой для левосторонней

области:

tлев,кр tпр,кр

3. H1 : a a0

Критическая область W – двусторонняя:

Пусть p(T t1,кр ) p(T t2,кр ) / 2

В силу чётности плотности распределения Стьюдента:

t1,кр t2,кр

Аналогично пунктам 1 и 2 получаем:

t	2,кр	F 1(1 / 2)	t		t	2,кр
		,	1,кр
		или
t		F 1( / 2)	t	2,кр	t
	1,кр	,				1,кр

Критерии, с помощью которых проверяется гипотеза о теоретическом законе распределения, называются

критериями согласия.

H0: генеральная совокупность имеет некоторое определённое распределение

(высказано предположение о виде и параметрах распределения)

1. Генеральная совокупность имеет биномиальное распределение с m=10 и p=0.4.

2. Генеральная совокупность распределена нормально с матаматическим ожиданием, равным 5 и дисперсией, равной 4.

Критерий Пирсона ( 2 -критерий)

Найдём теоретические частоты вариант.

1. Распределение дискретное				p(x).
xi	x1	x2	… xl-1	xl

pi p1=p(x1) p2=p(x2) … pl-1=p(xl-1) pl=1-p1-p2-…-pl-1 Теоретическая частота появления варианты xi – это npi.

2. Распределение непрерывное				F(x).
xi	(x1, x2)	(x2, x3)	…	(xl-1, xl)	(xl, xl+1)
pi	p1=p(X< x2)	p2=p(x2<X<x3)	…	pl-1=p(xl-1<X<xl) pl=1-p1-p2-
	=F(x2)	=F(x3)- F(x2)		=F(xl)- F(xl-1)	…-pl-1

Теоретическая частота попадания в интервал (xi, xi+1) – это npi.

		2	l	(n np )2
Критерий:				i	np	i
						i
			i 1

ni – эмпирические частоты npi – теоретические частоты

При n случайная величина 2 имеет распреде- ление Пирсона с k степенями свободы, где

k = l –1 –r,

l – число вариант (интервалов),

r – число параметров предполагаемого распределения, оцениваемых по выборке

Критическая область W – правосторонняя:

Из требования 1 для критической области:

	p( 2 W )	p( 2 кр2 )
p( 2 кр2	) 1 p( 2 кр2 ) 1
p( 2 2	) F( 2 )			2
кр	кр , F(x) – функция распределения
	F( кр2 ) 1		кр2 F 1(1 )

F(x) – функция распределения Пирсона с k=l–1–r степенями свободы, l – число вариант (интервалов), r – число параметров, оцениваемых по выборке.

Критерий Колмогорова

F(x) – теоретическая функция распределения Fn(x) – эмперическая функция распределения

Обозначим D max Fn (x) F(x)

– статистика критерия Колмогорова Критерий: Dn

Критическая область W – правосторонняя:

Из требования 1 для критической области:

p( W )
	p( кр ) p(D n кр )

Можно доказать, что при n

									2
		p(D		кр ) p( кр ) 1				( 1)k e 2k2 кр
			n
								k
					2
	1	( 1)k e 2k 2 кр						кр

k

	0.4	0.3	0.2	0.1	0.05	0.025	0.01	0.005	0.001	0.0005
кр	0.89	0.97	1.07	1.22	1.36	1.48	1.63	1.73	1.95	2.03

Критерий Фишера

Две генеральные совокупности X и Y распределены нормально.

Проверить гипотезу: H0 : D( X ) D(Y )

Обозначим nX – объём выборки из совокупности X, nY – объём выборки из совокупности Y,

s2X и s2Y – исправленные выборочные дисперсии.
Критерий:	F	s2X
		s2
		Y

F имеет распределение Фишера с (nX –1) и (nY –1) степенями свободы Критическая область строится в зависимости от вида конкурирующей гипотезы.

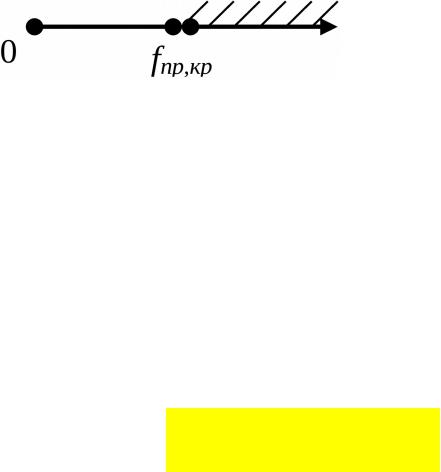
1. H1 : D( X ) D(Y )

Критическая область W – правосторонняя:

Так как s2X >0 и s2Y >0, то F >0 положительная часть Из требования 1 для критической области:

p(F W )		p(F fпр,кр )
p(F fпр,кр ) 1 p(F fпр,кр ) 1

p(F fпр,кр ) F( fпр,кр ), F(x) – функция распределения F

F( fпр,кр ) 1 fпр,кр F 1(1 )

F(x) – функция распределения Фишера с (nX –1) и (nY –1) степенями свободы

2. H1 : D( X ) D(Y )
Обозначим		1			s2		, F’ имеет распределение
					Y
	F F			s2X
								Фишера с (nY –1) и (nX –1)
								степенями свободы
H1 : D(Y ) D( X )		предыдущий случай:
							f		F 1(1 ),	где F(x) –
							пр,кр
							функция распределения F’
p(F f	)
пр,кр
p(F f	) p(1/ F f							) p(F 1/ f		)
пр,кр					пр,кр				пр,кр
			p(F 1/ fпр,кр )

p(F 1/ fпр,кр )
Обозначим f лев,кр 1/	fпр,кр , тогда

p(F f лев,кр )

Таким образом, критическая область для критерия F имеет вид:

		1				1
f лев,кр		f			1	(1 )
				F
		пр,кр

,где F(x) – функция распределения Фишера

с (nY –1) и (nX –1) степенями свободы

f2,кр

f1,кр

1

3. H1 : D( X ) D(Y )

Критическая область W – двусторонняя:

Пусть p(F f1,кр ) p(F f2,кр ) / 2

Аналогично пунктам 1 и 2 получаем:

f2,кр F1 1(1 / 2)

где F1(x) – функция распределения Фишера с (nX –1) и (nY –1) степенями свободы

1

F2 1(1 / 2)

где F2(x) – функция распределения Фишера с (nY –1) и (nX –1) степенями свободы