2.4. Линейная зависимость векторов

Выражение называетсялинейной комбинацией векторов с коэффициентамис₁, с₂, ..., с_n.

Система векторов называютсялинейно зависимой, если их линейная комбинация обращается в ноль прис₁, с₂, ..., с_n, не равных нулю одновременно; и линейно независимой, если только тогда, когда все коэффициентыс₁=с₂=...=с_n=0.

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Любые два неколлинеарных вектора линейно независимы. Любая система из трех векторов на плоскости линейно зависима.

Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Любые три некомпланарных вектора линейно независимы. Любая система из четырех векторов в пространстве линейно зависима.

2.5. Базис. Координаты вектора

Пусть V – векторное пространство. Базисом в пространстве V называется всякая система векторов , которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов).

Обозначим через V₁ – множество векторов на прямой; V₂ – множество векторов на плоскости; V₃ - множество векторов в пространстве.

Базисом в V₁ называется любой ненулевой вектор; в V₂ – любая пара неколлинеарных векторов; в V₃ – любая упорядоченная тройка некомпланарных векторов.

Теорема о разложении вектора по базису: Любой вектор можно разложить по базису единственным образом:

1. в V₁: ;

2. в V₂: ;

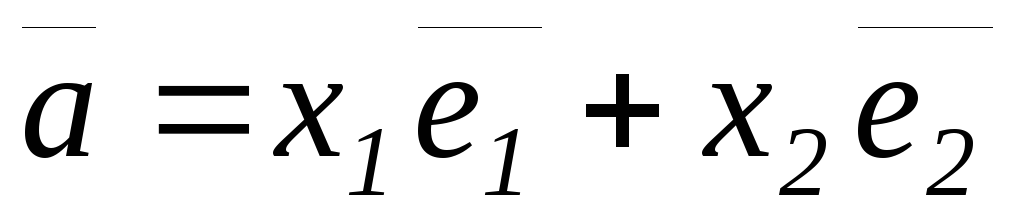3. в V₃: .

2.6. Прямоугольная (декартова) система координат

Системой прямоугольных (декартовых координат) называется совокупность точки O и базиса, обозначаемого и удовлетворяющего условиям:

1) =1;

2) ,

3) тройка векторов - правая.

Любой вектор можно представить в виде разложения по базису

:

,

числа х, у, z называются прямоугольными (декартовыми) координатами вектора .

Геометрический смысл координат вектора – координаты вектора есть проекции этого вектора на координатные оси:

х=;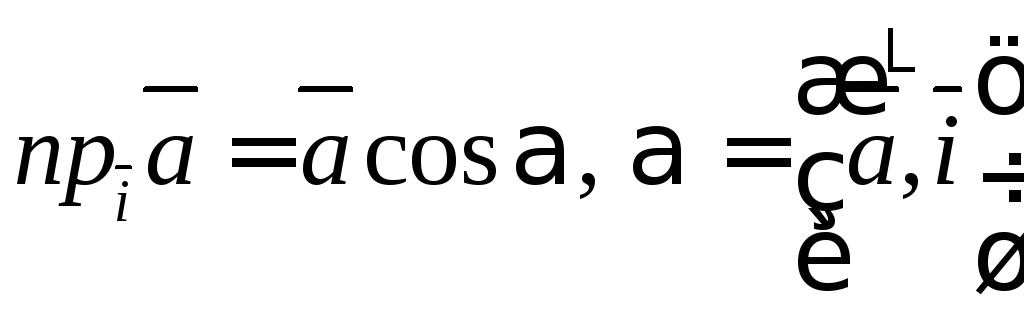

у=;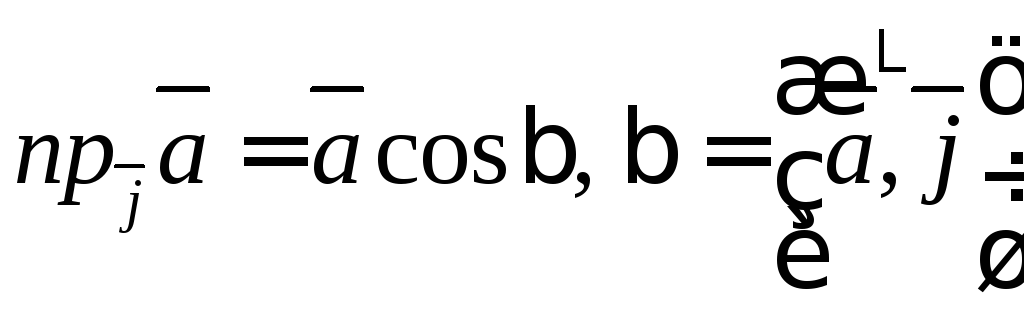

z=.

Cos, cos, cos - называются направляющими косинусами вектора.

Пусть даны точка М₁(х₁,у₁,z₁) и точка М₂(х₂,у₂,z₂), тогда вектор .

Координаты вектора .

Модуль вектора , равный расстоянию между точкамиМ₁ и М₂, находится по формуле:

.

Рассмотрим векторы (х_а; у_а; z_а) и (х_b; у_b; z_b), тогда

- если , то(х_а+х_b; у_а+у_b; z_а+z_b);

- если , то (х_а; у_а; z_а).

Условие коллинеарности векторов в координатной форме:

векторы иколлинеарны (=) тогда и только тогда, когда

.

Координаты середины отрезка М₁М₂:

.

2.7. Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:

.

Алгебраические свойства скалярного произведения:

1) - свойство коммутативности;

2) - скалярное произведение вектора на себя равно квадрату модуля вектора;

3) ()=()– свойство ассоциативности;

4) (+)=+- свойство дистрибутивности.

Геометрические свойства скалярного произведения:

1) тогда и только тогда, когда=0 – условие ортогональности векторов;

2) Два ненулевых вектора исоставляют:

• острый угол, если 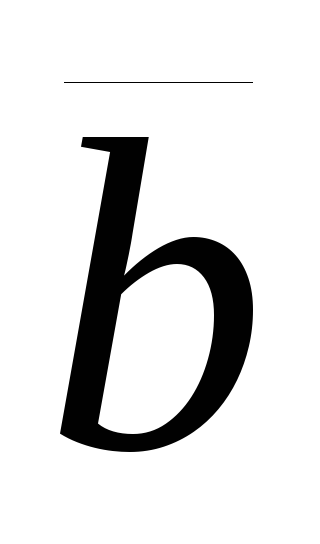>0;

• тупой угол, если <0;

Скалярное произведение в координатах двух векторов (х_а;у_а;z_а) и (х_b;у_b;z_b) есть число, равное сумме произведений одноименных координат:

=x_ax_b+y_ay_b+z_az_b.

Из определения скалярного произведения вытекают следующие формулы:

- косинус угла между векторами ;

- проекция вектора на векторравна.