Обратная матрица.

Вспомнить понятия противоположных и обратных чисел

Пусть - квадратная матрица порядка.

Определение 1.13. Матрица называется обратной к матрице, если имеет место равенство

.

Из определения следует, что также является квадратной порядка.

Замечание. Понятие обратной матрицы вводится только для квадратных матриц, однако не для каждой квадратной матрицы существует обратная. Приведём критерий существования обратной матрицы.

Определение 1.14. Матрица называется невырожденной, если её определитель отличен от нуля (). В противном случае матрицаназывается вырожденной.

Определение 1.15. Матрица , состоящая из алгебраических дополнений к элементам матрицы, называется союзной (или присоединённой) к.

Теорема 1.1. Для существования у матрицы обратной матрицы необходимо и достаточно, чтобы матрицабыла невырожденной.

Доказательство. Необходимость (известно, что существует матрица, обратная к ; надо показать, что определительотличен от нуля). По определению обратной матрицы. По свойству 7 определителей, следовательно каждый из определителейиотличен от нуля.

Достаточность (известно, что определитель отличен от нуля; надо показать, что существует матрица, обратная к) Рассмотрим матрицу. По следствию из свойства 6 определителей=, следовательно- диагональная матрица вида

и, кроме того, . Таким образом, матрицаявляется обратной к матрице, поскольку.

Замечание. Из доказательства теоремы вытекает схема нахождения матрицы, обратной к матрице : 1) вычислитьи убедится, что он отличен от нуля (в противном случае обратной матрицы не существует); 2) найти союзную матрицу(матрицу из алгебраических дополнений; 3) записать матрицу, пользуясь формулой; 4) сделать проверку, подставив полученное значениев соотношение(определение обратной матрицы).

Пример 1.7. Пусть .Найти.

Решение. 1) (смотри пример 1.6), следовательно, обратная матрица существует; 2);;;

; ;;

; ;;

Таким образом, =,и, следовательно,

3) =. Проверку выполнить самостоятельно!

Системы линейных алгебраических уравнений.

Определение 1.16. Системой линейных алгебраических уравнений снеизвестными называется система вида

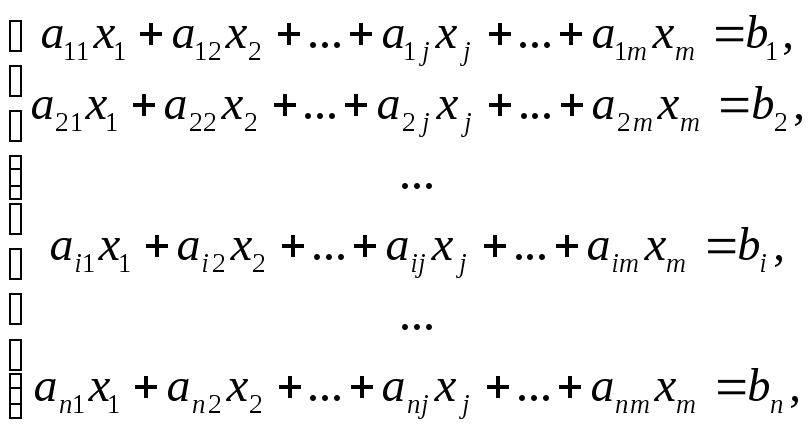(1)

где - произвольные числа, называемые коэффициентами при переменных и свободными членами соответственно.

Определение 1.17. Решением системы (1) называется упорядоченный набор чисел, при подстановке которых в систему вместо неизвестных получаетсятождеств.

Замечание. СЛАУ может либо иметь одно решение, либо иметь бесконечно много решений, либо не иметь ни одного решения. Это легко показать на примере системы двух уравнений с двумя неизвестными – две прямые на плоскости могут либо пересекаться в одной точке, либо совпадать, либо не иметь общих точек.

Определение 1.18. Система называется совместной, если имеет хотя бы одно решение (несовместной, если не имеет решений). Совместная система называется определённой, если имеет единственное решение (неопределённой, если бесконечное множество).

Пример 1.8. - определённая,- неопределённая,

- несовместная.

Систему (1) можно записать в матричной форме

, (2)

где - матрица коэффициентов при неизвестных,- вектор – столбец неизвестных,- вектор – столбец свободных членов.

Рассмотрим условия существования решений систем, у которых число неизвестных совпадает с числом уравнений.

Теорема 1.2. Пусть и матрицаявляется невырожденной. Тогда у системы (2) существует единственное решение, определяемое формулой.

Доказательство. Так как , то существует матрица. Домножив слева соотношениена, получим.

Теорема (правило Крамера). Пусть и матрицаявляется невырожденной. Тогда у системы (2) существует единственное решение, определяемое формулами

,

где ,- определители матриц, получаемых из матрицызаменой- го столбца на столбец свободных членов.

Доказательство. Распишем формулу в развёрнутом виде

,

то есть или, с учётом теоремы Лапласа,.

Пример 1.9. Вкладчик банка положил на два разных счёта 1 200 гривен. По первому счёту банк начисляет 6% годовых, по второму – 8%. По истечению года вкладчик получил 80 гривен процентных денег. Как были распределены средства по счетам?

Решение. Пусть х₁ – сумма, размещённая на первом счету, х₂ – на втором. Тогда имеет место система соотношений

.

Метод Крамера: ,,,,. Таким образ получили, что вкладчик положил 800 гривен на первый счёт и 400 гривен на второй;

Матричный метод: и.

Замечание. К недостаткам метода Крамера и матричного метода решения СЛАУ можно отнести следующее: а) они применимы лишь в случае, когда матрица коэффициентов при переменных квадратная и невырожденная; б) даже в этом случае их применение связано с громоздкими вычислениями (исключение - постоянна,меняется – оправданно применение матричного метода). Поэтому необходимо изучить метод, свободный от этих недостатков.

Метод Гаусса (последовательного исключения переменных).

Рассмотрим СЛАУ вида (1). Выпишем расширенную матрицу коэффициентов данной системы

и с помощью элементарных преобразований (над строками) приведём её к одному из двух видов

или ,

где при(треугольному или ступенчатому соответственно).

Треугольный вид. Если при выполняется, то исходная система не имеет решений (поскольку в- ой строке получается неверное равенство). Если же привыполняется, то система имеет единственное решение.

Пример 1.10. Решить систему уравнений

Решение. Выпишем расширенную матрицу системы, домножив (для удобства вычислений) первую и третью строки на

.

Выпишем систему, соответствующую последней матрице

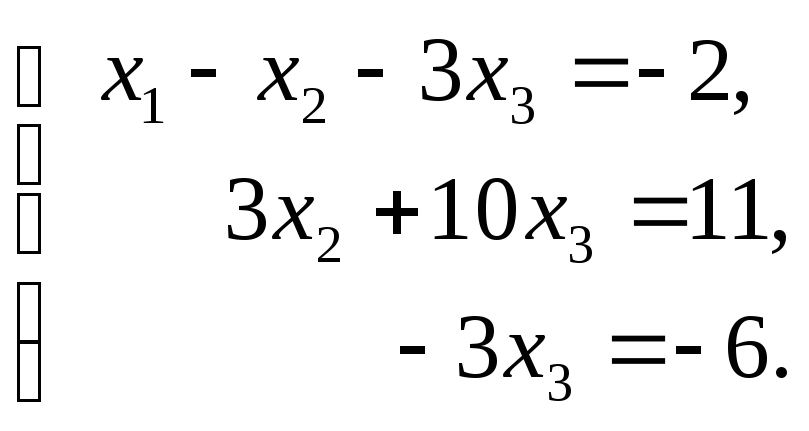
Из третьей строки находим . Подставив это значение во вторую строку, получим. В свою очередь, подставив значенияив первую строку, получим.

Ответ. .

Ступенчатый вид. Если при выполняется, то исходная система не имеет решений. Если же привыполняется, то у системы бесконечно много решений. При этом первыепеременных называются базисными, а оставшиеся– свободными. Выразив базисные переменные через свободные, получим общее решение системы. Придавая свободным переменным фиксированные значения, получаем частные решения системы. Частное решение, в котором все свободные переменные равны нулю, называется базисным.

Пример 1.11. Решить систему уравнений

Решение. Составим расширенную матрицу данной системы и преобразуем её

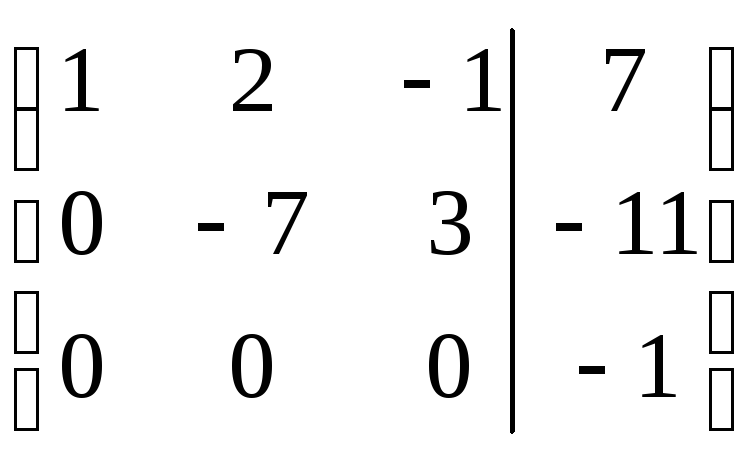
из вида последней строки вытекает, что у системы нет решений.

Пример 1.12. Решить систему уравнений .

Решение. Запишем расширенную матрицу системы, поменяв (для удобства вычислений) местами первую и вторую строки

.

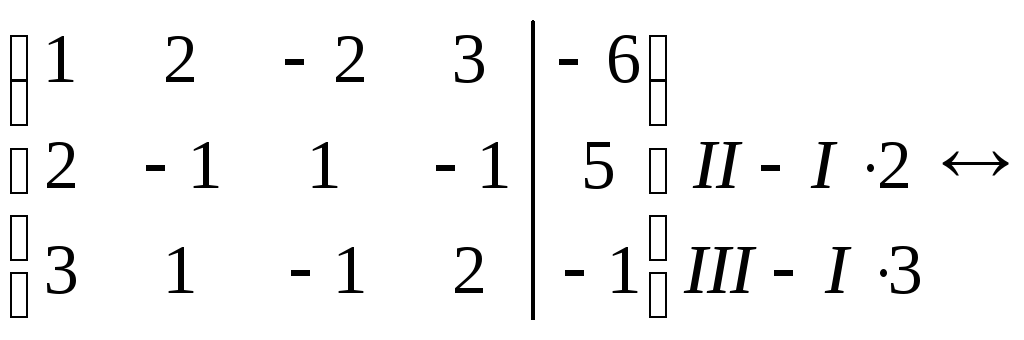
Выпишем систему, соответствующую последней матрице

У данной системы 4 неизвестных и 2 уравнения, следовательно, число свободных переменных 4-2 = 2 – две, пусть это будут и, тогдаи.

Ответ. - общее решение,- базисное решение

Замечание. Если при приведении матрицы к виду (1) или (2) необходимо поменять местами столбцы l и k (элемент на главной диагонали и все под ним равны нулю), то в дальнейшем при выписывании системы переменныеx_l и x_k также необходимо поменять местами.

9