Высшая математика / 2 / shpory_k_ekzamenu

11. Локальная теорема Муавра-Лапласа. Пусть число испытаний n достаточно велико, а вероятность p наступления события A в каждом испытании не близко ни к нулю, ни к единице, тогда имеет место приближенное равенство. , где

Функция называется функцией Гаусса. Ее значения протабулированы. Пользуясь таблицей, следует учитывать: 1.Функция 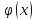четная, т.е. ; 2.При x>4 можно считать =0.

12. Интегральная теорема Муавра-Лапласа. Пусть число испытаний n достаточно велико, а вероятность p наступления события A в каждом испытании не близко ни к нулю, ни к единице, тогда вероятность того, что событие A появится не менее К₁ раз, но не более К₂ раз находится по формуле: , где , . Для упрощения вычислений вводят специальную функцию , которая называется функцией Лапласа и в этом случае формулу можно переписать: . Значение функции Лапласа протабулировано. Пользуясь таблицей, следует учитывать: 1.Функция нечетная, т.е. 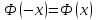; 2.При x>4 можно считать =0,5.

13. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях. Обозначим через m число появлений события A в n независимых испытаниях, в каждом из которых вероятность наступления этого события постоянна и равна p (соответственно вероятность непоявления также постоянна и равна q=1-p). Найдем вероятность того, что отклонения относительной частоты m/n от постоянной вероятности p по абсолютной величине не превышает заданного числа Ɛ > 0, т.е. найдем вероятность того, что осуществляется неравенство: .

, т.е. вероятность того, что отклонение относительной частоты от постоянной вероятности не превысит заданного числа Ɛ > 0, приближенно равна удвоенной функции Лапласа с аргументом .

14. Понятие случайной величины. Случайной величиной называется величина, которая в результате эксперимента принимает то или иное значение, причем заранее неизвестно, какое именно. Случайные величины обозначаем большими латинскими буквами (X, Y, Z), а принимаемые ими значения соответственно маленькими буквами (x₁, y₁ и т.д.). Дискретной называют случайную величину, которая принимает отдельные изолированные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Если известен способ нахождения вероятностей, с которыми СВ принимает свои значения, то говорят, что задан закон распределения этой случайной величины.

15. Закон распределения дискретной СВ. Пусть дискретная СВ X принимает конечное или счетное число значений x₁, x₂ … x_n … с вероятностями p₁, p₂ … p_n … . В этом случае закон распределения дискретной СВ удобно задавать в виде ряда распределения:

xi	x1	x2	…	xn	…
pi	p1	p2	…	pn	…

Т.к. значения x_i несовместимы и образуют полную группу, то сумма их вероятностей равна 1. Закон распределения дискретной СВ можно задать графически в виде ломаной, последовательно соединяющей точки (x₁p₁; x₂p₂; … ; x_np_n; …). Ломаная называется многоугольником распределения.

16. Математическое ожидание дискретной СВ и егpоi свойства. Пусть дискретная СВ X задана рядом распределения:

x	x1	x2	…	xn	…
p	p1	p2	…	pn	…

Математическим ожиданием дискретной СВ X называется число, равное сумме произведений всех ее значений соответствующей вероятности: . Вероятностный смысл мат.ожидания: мат.ожидание приближенно равно среднему арифметическому наблюдаемых значений СВ. Поэтому его часто называют центром распределения.

Свойства мат.ожидания: 1.M(k)=k, k=const; 2.M(k*x)=k*M(x); 3.M(x+k)=M(x)+M(k); 4.M(x-M(x))=0; 5.M(xy)=M(x)*M(y), где x,y – независимые величины

17. Дисперсия дискретной СВ и ее свойства. Среднее квадратическое отклонение. Дисперсией дискретной СВ X называется мат.ожидание квадрата ее отклонения от своего мат.ожидания: ; . На практике удобно пользоваться формулой: , где . Свойства дисперсии: 1.Д(k)=0, k=const; 2.Д(kx)=k²*Д(x); 3.Д(x±y)=Д(y)±Д(x); 4.Д(x+k)=Д(x); 5.Д(xy)=M(x²)*M(y²)-(M(x))²*(M(y))², x,y – независимые величины.

Дисперсия СВ X имеет размерность квадрата СВ X, что в сравнительных целях неудобно. Когда желательно, чтобы оценка разброса имела размерность СВ используют еще одну характеристику: среднее квадратическое отклонение.

18. Функция распределения и ее свойства. Пусть X – действительное число. Вероятность события, состоящая в том, что СВ X примет значение <x, обозначим через F(x). Очевидно, что при изменении x будет меняться и F(x), т.е. F(x) – функция, зависящая от x. Функцией распределения СВ X называется функция

Свойства функции распределения: 1.0≤F(x)≤1; 2.F(x) – неубывающая функция; 3.; 4.; 5.F(x) непрерывна слева. Эти свойства являются общими для дискретной и непрерывной СВ.

19. Плотность распределения вероятностей и ее свойства. Плотностью распределения вероятностей непрерывной СВ X называется производная от ее функции распределения: f(x)=F’(x). Свойства плотности распределения: 1.f(x)≥0; 2.; 3.;4.;5.

20. Числовые характеристики непрерывной СВ: 1.Математическое ожидание: ; 2.Дисперсия: ; 3.Среднее квадратическое отклонение: .