Потенциальная ступень.

Потенциальной ступенью называется ограниченная параллельными плоскостями область пространства, в которой потенциальная функция U(x) больше, чем в прилегающих областях.

Рассмотрим поведение частицы на границе областей 1 и 2, где потенциальная функция меняется скачком, примем U₁=0 иU₂=U₀.

Рассмотрим случай когда E>U₀

по классической физике частица пролетит, а в квантовой физике возможны варианты.

Для каждой области 1 и2 составим уравнения Шредингера(одномерное):

1. d²Ψ₁/dx²+(2m/Ћ²)EΨ₁=0

2. d²Ψ₂/dx²+(2m/Ћ²)(E-U)Ψ₂=0

Обозначим (2m/Ћ²)Е=k², тогда

K₁=/Ћ=p/Ћ=2π/λ₁, гдеλ₁- длина волны де Бройля в 1ой области.

К₂=/Ћ=p/Ћ=2π/λ₂, гдеλ₂- длина волны де Бройля во второй области.

Ψ₁”-k²Ψ₁=0 (3)

Ψ₂”-k²Ψ₂=0 (4)

Решение уравнения Шредингера (3)и (4) будем искать в показательной форме.

Ψ₁=A₁exp(ik₁x)+B₁exp(-ik₁x)

Ψ₂=A₂exp(ik₂x)+B₂exp(-ik₂x), где

A₁-это амплитуда падающей на ступень волны,

В₁-это амплитуда отраженной от ступени волны,

А2-это амплитуда, прошедшей через ступень волны,

В₂=0, т.к. не будет отражения

exp(ikx) принадлежит проходящей волне

exp(-ikx) принадлежит отраженной волне

Тогда движение электрона представляется плоской волной де Бройля на границе ступени. где происходит внезапный рост потенциальной энергии эта волна должна вести себя так как ведёт себя световая волна на границе двух сред с различными показателями преломления, следовательно на границе волна де Бройля частично отражается в первую область, а частично проходит во вторую область. Найдём вероятность, с которой волна отразится и вероятность, с которой волна будет проходить.

Для решения этих задач необходимо воспользоваться свойствами волн де Бройля и свойствами волновой функции. при которой функция на границе двух сред непрерывна, а также непрерывна её первая производная .

На границе двух сред функция непрерывна, значит в 1ой области x<0, а во второй областиx>0. В т.0 функция должна быть непрерывна и мы получаем:

А₁+В₁=А₂

должны быть равны ещё и первые производные в т. x=0 возьмём первую производную по (3) и (4), подставляемx=0 и получим:

K₁(1-B₁)=K₂A₂

получаем систему:

А₁+В₁=А₂

K₁(1-B₁)=K₂A₂

Принято А₁принимать равным 1, тогда

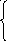
1+В₁=А₂

K₁-К₁B₁=K₂A₂

В₁=(K₁-K₂)/(K₁+K₂)

A₂=2K₁/(K₁+K₂)

Пользуясь аналогией с оптикой, определим коэффициент отражения ρи коэффициент прохождения(прозрачности)

ρ=отношение квадратов амплитуд отраженной и падающей волн:

ρ=B₁²/A₁²

= отношение квадратов амплитуд прошедшей и падающей волны

=A₂²/A₁²

Получаем ρ=(K₁-K₂)²/(K₁+K₂)²

=4K₁K₂/(K₁+K₂)²

По закону сохранения вещества ρ+=1

По законам классической физики электрон пройдёт, а в квантовой физике есть вероятность. что электрон будет отражён.

Потенциальный барьер конечной ширины.

В классической физике частица пролететь не может, а в квантовой есть вероятность, что электрон окажется в области 2.

E<U0

Вероятность прохождения частицы через барьер (или прозрачность барьера(D)) определяется отношением вероятности обнаружить частицу в точкеx=dза барьером к вероятности в точкеx=0 перед барьером:

ω=dω₃(d)/dω₁(0)

dω₁(0)=|Ψ₁(0)|²dx

dω₃(d)= |Ψ₃(d)|²dx

ω=|Ψ₃(d)|²dx/|Ψ₁(0)|²dx=|Ψ₃(d)|²/|Ψ₁(0)|²

т.е. задача сводится к нахождению волновых функций 1 и 3. Для каждой из областей запишем своё уравнение Шредингера:

1) d²Ψ₁/dx²+(2m/Ћ²)EΨ₁=0

d²Ψ₂/dx²+(2m/Ћ²)(E-U₀)Ψ₂=0 - во второй области есть сначала потенциальная энергия.

d²Ψ₃/dx²+(2m/Ћ²)EΨ₃=0

Введём обозначения К1 и К2:

K₁=/Ћ

К₂=₀)/Ћ

K₃=/Ћ

Исходные уравнения запишутся в виде:

Ψ₁”+k²Ψ₁=0

Ψ₂”-k²Ψ₂=0

Ψ₃”+k²Ψ₃=0

Решение этих уравнений будем искать в показательной форме:

Ψ₁=A₁exp(ik₁x)+B₁exp(-ik₁x)

Ψ₂=A₂exp(-ik₂x)+B₂exp(+ik₂x),

Ψ₃=A₃exp(ik₃x)+B₃exp(-ik₃x)

exp(ikx) соответствует волне, распространяющейся в положительном направлении осиx

exp(-ikx) в противоположном направлении

А1-амплитуда волны падающей справа на барьер

В1-амплитуда волны, прошедшей через барьер в третью область

В2-амплитуда волны, отраженной от барьера в точке x=d

A3-амплитуда волны, прошедшей через барьер в точкеx=d

В3=0 (т.к. как ничего не отражалось)

Не будем учитывать отраженные волны, тогда пси-функции упрощаются:

Ψ₁=A₁exp(ik₁x)

Ψ₂=A₂exp(-ik₂x)

Ψ₃=A₃exp(ik₃x)

Здесь пси-функции содержат мнимую единицу. Вспомним что |Ψ|²=Ψ·Ψ^*

|Ψ₁|²= A₁exp(ik₁x)· A₁exp(-ik₁x)=A₁²

|Ψ₃|²= A₃exp(ik₃x)· A₃exp(-ik₃x)=A₃²

тогда ω=A₃²/A₁²

В области барьера пси-функция действительна, учтём непрерывность пси-функции на границе, тогда в точке x=0 А₁≈А₂и в точкеx=dА₃=А₂·exp(-K₂d), тогда

ω= A₃²/ A₁²= А₂·exp(-K₂d)/ А₂= exp(-K₂d)

Вспомним, что К₂=₀)/Ћ, тогда

ω=exp((-2/Ћ)d)

Все химические реакции основаны на преодолении потенциального барьера.