Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах

областю визначення багатофакторної ВФ f x1, ,xn є безліч n-

мірних векторів Х, усі координати x1,...,xn яких невід’ємні числа.

Для окремого підприємства (фірми), що випускає однорідний продукт, ВФ f x1, ,xn може зв'язувати обсяг випуску (у натуральному або вартісному вираженні) з витратами робочого часу за різними видами трудової діяльності, різними видами сировини, комплектуючих виробів, енергії, основного капіталу (вимірюваних в натуральних одиницях). ВФ такого типу характеризують діючу технологію підприємства (фірми). Найчастіше використовуються виробничі функції з двома ресурсами: працею L і капіталом К.

За аналогією виробничі функції можна класифікувати таким чином:

лінійні виробничі функції (ЛВФ) з різним числом факторів,

наприклад, лінійна виробнича функція вигляду y a1x1 a2x2 , де параметри a1 і a2 виражають продуктивність факторів x1 і x2, тобто показують абсолютний приріст виробництва, коли один із факторів залишається незмінним, а інший зростає на одиницю. Лінійні функції часто застосовуються в короткострокових і середньострокових комплексних економетричних моделях. При середньостроковому аналізі вивчають багатофакторні лінійні виробничі функції, що включають залежність зростання продуктивності праці, ефективність основних засобів виробництва і т. ін.

Властивості:

1)f 0,0 0;

2)x1 x 0 f x1 f x 0 , x k x1 k ,x2 k , k 0,1 ;

2а`) x

0

f x

0, i

,

x x1, x2 ;

1,2

xi

2б) граничні продуктивності чинників є постійними:

y

a ,

y

a

2

;

x

x

1

2

1

2в) гранична продуктивність одного з чинників є постійною і функція однорідна першого степеня:

ftx1,tx2 tf x1,x2 .

степеневі виробничі функції, серед яких найбільш відома

виробнича функція Кобба Дугласа (ВФКД). Ця функція має вигляд:

y a0x1a1 x2a2 , a1 a2 1.

Параметри a1 і a2 виражають еластичність рівня виробництва y стосовно факторів x1 і x2, тобто показують відносний приріст

11

продукції (у відсотках), пов'язаний з відносним приростом основних фондів і робочої сили.

Властивості:

1)	f 0,0 0;
1а) f 0,x2 f x1,0 0;
2)	x1 x 0 f x1 f x 0 , x k x1 k ,x2 k , k 0,1 ;
2а`) xi				0				f X					0,	i					,	X	x , x				;
																	1,2							2
								xi															1
	xi						2 f X													X	x1, x2			;
														i 1,2,
3)			0									0,
								xi2
3а) x			0		2 f X				0,				i		X x ,x								;
		i												1,2,								2
					x1 ›2															1

4)	f tx ,tx	2	tp f x ,x .
	1		1	2

виробнича функція Леонтьева:

y min a1x1,a2 x2 .

Властивості (див. властивості ВФКД).

 більш складні типи виробничих функцій, серед яких найбільш відома функція з постійною еластичністю заміни, так звана функція CES.

Властивість (1) означає, що без ресурсів немає випуску. Властивість (1а) означає, що за відсутності хоча б одного з ресурсів немає випуску. Властивість (2) означає, що зі зростанням витрат хоча б одного ресурсу обсяг випуску зростає.

Властивість (2а) (перша частинна похідна виробничої функції

f X

додатна), означає, що зі зростанням витрат одного ресурсу

xi

при незмінній кількості іншого ресурсу обсяг випуску зростає. Упорядковану пару (x1,x2) чисел x1 і x2 позначимо символом X ,

тобто X (x1,x2).

Властивість (3) (друга частинна похідна виробничої функції

		2	f	X
						недодатна) означає, що зі зростанням витрат одного
			x	2
				i

12

(i-го) ресурсу при незмінній кількості іншого ресурсу величина приросту випуску на кожну додаткову одиницю i-го ресурсу не зростає (закон спадаючої ефективності).

Властивість (3а) означає, що при зростанні одного ресурсу гранична ефективність іншого ресурсу зростає.

Властивість (4) означає, що ВФ є однорідною функцією (ОФ) ступеня p ( p 0). При p 1 зі зростанням обсягу виробництва в t

разів (число t>1), тобто з переходом від вектора X до вектора tX ,

обсяг випуску зростає в t p t разів, тобто отримаємо функцію, що відображає зростання ефективності виробництва від зростання масштабу виробництва. При p 1 маємо спад ефективності виробництва від зростання масштабу виробництва. При p 1 маємо постійну ефективність виробництва при зростанні його масштабу (або маємо незалежність питомого випуску від масштабу виробництва - в англійській термінології constant returns to scale).

Лінія рівня lq, q f (x1,x2)	(0 q	- дійсне число) ВФ
y f (x1,x2) називається ізоквантою ВФ.		Іншими словами, лінія

рівня lq - це множина точок, в яких ВФ постійна і дорівнює q. Різні набори (v1,v2) і (w1,w2) затрачених (використаних) ресурсів, що належать одній і тій самій ізокванті lq (тобто q f (v1,v2) f (w1,w2)), дають один і той самий обсяг випуску q.

Ізокванта це	лінія, розташована в	невід’ємному октанті
(x1,x2)| x1 0,	x2 0 двомірної площини Ox1x2.
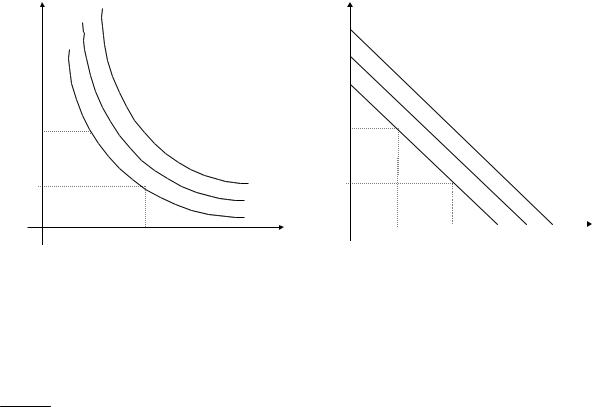
На рис. 1.1 наведені ескізи ізоквант lq1		і lq2 ВФКД. Зазначимо,

що ізокванта lq2, розташована "північніше" ізокванти lq1, відповідає

більшому обсягу випуску	(тобто	q2 q1).	Якщо	обсяг
використовуваного основного	капіталу	необмежено	зростає	(тобто

x1 K ), то, як видно на рис. 1.1, витрати праці необмежено зменшуються (тобто x2 L 0). Аналогічно, як видно на рис. 1.1,

якщо x2 L , то x1 K 0. На рис. 1.2 показані ескізи ізоквант lq1 і lq2 ЛВФ.

При n 2 для будь-якої ВФ, для якої справедливі всі (або частина) властивостей (1) – (4), ізокванта (якщо вона не є прямою) є лінія (не обов'язково гладка), що опукла до точки O, тобто лінія, що схожа на ізокванту lq рис. 1.1.

13

x2

x2

w2			w2
v2		lq2	v2
		lq1
		l q		0			lq lq 1 lq2 x1
0	w1	v1	x1		w1	v1
	Рис.1.1				Рис.1.2
Граничні (маргінальні) і середні значення виробничої
функції.	Нехай	y f (X) f (x1,x2)		-	виробнича	функція. Дріб

f (X) , i 1,2 називається середньою продуктивністю i-го ресурсу

xi

(фактора виробництва) (СВФ) або середнім випуском за i-м ресурсом

(фактором виробництва). Позначення: A					f (X)	.
				i	xi
Зазначимо, що у випадку двофакторної ВФКД Y a0Ka1 La2
	Y	Y
для середніх продуктивностей		і		— основного капіталу і праці
	K
			L

використовують відповідно терміни капіталовіддача і продуктивність праці. Ці терміни використовують і стосовно до будь-яких двофакторних ВФ, для яких x1 K і x2 L.

Нехай y f (x) f (x1,x2) — ВФ. Її перша частинна похідна:

M	i		f (x)	,	i 1,2
			x
			i

називається граничною (маргінальною) продуктивністю i-го ресурсу (фактора виробництва) (ГПФ) або граничним випуском за i-м ресурсом (фактором виробництва).

Позначимо символами xi і i( f (x))

( 1( f (x1,x2)) f (x1 x1,x2) f (x1,x2),

14

2( f (x1,x2)) f (x1,x2			x2) f (x1,x2))				відповідно,
збільшення змінної		x1 і	x2 відповідне			їй часткове	збільшення ВФ
f (X). При малих xi		маємо наближену рівність:
	f (X )			i f (X )	,	i 1,2 .
		xi
				xi

Отже, ГПФ (наближено) показує, на скільки одиниць збільшиться обсяг випуску y, якщо обсяг витрат xi i-го ресурсу виростає на одну (досить малу) одиницю при незмінних обсягах

іншого витраченого ресурсу. Тут граничну величину f ( X )

x i

(тобто ГПФ) доцільно інтерпретувати, використовуючи близьке до неї відношення малих скінченних величин, тобто i( f (X)) і xi .

Зазначена обставина є ключовою для розуміння економічного змісту

ГПФ	f (	X )	. Інші	граничні величини варто			інтерпретувати
	x i
аналогічним чином.							X (x1,x2).
Нехай		y f (X)		-	виробнича	функція,
Відношення		граничної продуктивності Mi				i-го ресурсу до його
середньої продуктивності				Ai	називається (частинною) еластичністю

випуску за i-м ресурсом (за фактором виробництва) (ЕВФ). Позначення:

Ei	M i		xi		f (X )		,	(i 1,2) .
	A		f (X )		x	i
	i

Сума Е1+Е2=Еx називається еластичністю виробництва. Оскільки при малому збільшенні хi маємо наближену рівність:

f (X)

i f (X)

Ei

xi

f (X)

,

f (X)

xi

xi

xi

то Ei (наближено) показує, наскільки відсотків збільшиться випуск y, якщо витрати i-го ресурсу збільшаться на один відсоток при незмінних обсягах іншого ресурсу. Пояснення виразу Еi, що містить

f (X)

граничну величину , за допомогою виразу, що містить

xi

15

скінчене наближення i f (X) цієї граничної величини, є ключовим у

f (X)

розумінні економічної суті частинної еластичності випуску за i-м ресурсом.

Нехай y f (X) - виробнича функція, X (x1,x2). Граничною нормою заміни i-го ресурсу (фактора виробництва) j-м

(скорочено: ГНЗФ і позначення: Rij ) називається вираз:

R	dxj	,	i,j 1,2	(1.3)
ij	dxi

при постійній у. Зазначимо, що і - номер ресурсу, що замінюють, j- номер ресурсу, що заміщає. Використовується також термін: «гранична технологічна норма» заміни i-ого ресурсу (фактора виробництва) j-м ресурсом (фактором виробництва). Наведемо більш короткий (але менш точний) термін: (гранична) норма заміни ресурсів.

Для двофакторної ВФ справедлива рівність:

R12 E1 x2 ,

E2 x1

тобто (гранична) норма заміни першого ресурсу другим дорівнює відношенню еластичностей випуску за першим і другим ресурсом, помноженому на відношення обсягу другого ресурсу до обсягу

першого ресурсу. Якщо x K,	x	2	L, то відношення	x1		K
1				x2		L

називається капіталоозброєністю праці.

У цьому випадку (гранична) норма заміни основного капіталу працею дорівнює відношенню еластичностей випуску за основним капіталом і працею, поділеному на капіталоозброєність праці.

Нехай ВФ – двофакторна функція. Тоді при постійному випуску і малих приростах x1 і x2 маємо наближену рівність:

R	dx2		x2	.	(1.4)
12	dx1		x1

На підставі відношення (1.4) (гранична) норма заміни ресурсів R12 (наближено) показує, на скільки одиниць збільшаться витрати другого ресурсу (при незмінному випуску y a), якщо витрати першого ресурсу зменшаться на одну (малу) одиницю.

16

1.2. Математична теорія фірми

При аналізі фінансової діяльності підприємств зручно використовувати модель фірми. Розглянемо основні положення цієї моделі. Детально моделювання поведінки виробників розглянуто у підручнику [8] . Фірма являє собою деяку організаційну одиницю, у рамках якої приймаються ефективні рішення [8]. Застосовуючи слово “фірма”, розуміють також підприємство, завод, компанія.

Будь-яка фірма в ході своєї діяльності повинна вирішувати ряд завдань. Що і в якій кількості виробляти? Як виробити свою продукцію? За якою ціною реалізовувати продукцію? Відповіді на ці та інші питання дають змогу припустити, що метою фірми є максимізація її прибутку.

Доходом (виручкою) R фірми у визначеному часовому періоді (наприклад, у визначеному році) називається добуток p0y від загального обсягу y продукції, що випускається фірмою, на (ринкову)

ціну p0 цієї продукції.

Витратами C фірми називають загальні виплати фірми у визначеному часовому періоді за всі види витрат C p1x1 p2x2, де x1 і x2 - обсяги затрачуваних фірмою ресурсів (факторів виробництва), p1 і p2 - ринкові ціни на ці ресурси (фактори виробництва).

Прибутком F фірми у визначеному часовому періоді

називається різниця між отриманим фірмою доходом		R та її
витратами на виробництво:
	F R C,	(1.5)
або	F(x1,x2) p0 f (x1,x2) (p1x1 p2x2)	(1.6).
Остання	рівність виражає прибуток фірми у	термінах

затрачуваних ресурсів. y f x1,x2 - виробнича функція фірми, що виражає загальний обсяг y продукції, що випускається фірмою, через обсяги x1 і x2, затрачуваних ресурсів.

Якщо фірма функціонує в умовах чистої (досконалої) конкуренції, то на ринкові ціни p0, p1, p2 вона впливати не може.

Фірма “погоджується” з цінами p0, p1, p2.

Основна мета фірми полягає в максимізації прибутку шляхом раціонального розподілу затрачуваних ресурсів. Формально задача максимізації прибутку у визначеному часовому періоді має вигляд: F max. Така постановка задачі максимізації залежить від того, який конкретно часовий проміжок (довгостроковий або короткостроковий) передує періодові, у якому фірма максимізує свій прибуток.

17

У випадку довгострокового проміжку фірма може вільно вибирати будь-який вектор X (x1,x2) витрат із простору витрат

(формально з невід’ємного октанта x1 0, x2 0 площини Ox1x2), тому задача максимізації прибутку у випадку довгострокового проміжку має такий вигляд:

p0 f x1,x2 p1x1 p2x2 F x1,x2 max		(1.7)
за умови, що
x1 0,x2	0,	(1.8)

(постановка задачі в термінах затрачуваних ресурсів).

У випадку короткострокового проміжку фірма повинна враховувати неминучі ліміти на обсяги затрачуваних (використовуваних) нею ресурсів, що формально можуть бути записані у вигляді нелінійної нерівності g x1,x2 b, (обмежень

вигляду g x1,x2 b може бути декілька). Отже, задача максимізації прибутку для короткострокового проміжку має вигляд задачі математичного програмування:

p0 f x1,x2 p1x1 p2x2 F x1,x2 max	(1.9)
за умови, що:
g x1,x2 b,	(1.10)
x1 0, x2 0,	(1.11)

(постановка задачі в термінах затрачуваних (використовуваних) ресурсів).

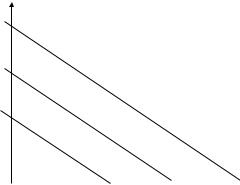
Лінія рівня p1x1 p2x2 функції витрат виробництва називається ізокостою (рис.1.3).

x2

2

1

0

x1

O

Рис.1.3

18

Функції попиту на фактори (ресурси) у випадках короткострокового і довгострокового періодів. У випадках

довгострокового проміжку задача максимізації прибутку (1.7) являє собою звичайну задачу на глобальний абсолютний максимум при

x1 0 і x2 0. Вектор x10 , x 02 витрат ресурсів, що є розв’язком задачі максимізації прибутку F, називається локальною (частковою) ринковою рівновагою фірми (у випадку довгострокового проміжку).

Можна показати, що в точці x10 , x 02 локальної ринкової

рівноваги фірми гранична норма заміни R12 x10,x20 першого ресурсу другим дорівнює відношенню p1 p2 ринкових цін на ці ресурси:

	f		x	0	,x	0
			1			2
			x1
R12	f		x	0	,x	0			p1 p2	(1.12).
			1			2

x2

Наслідком виразу (1.12) є наступне твердження: у точці локальної ринкової рівноваги фірми нахил дотичної до ізокванти

повинен дорівнювати нахилу ізокости. Координати x10 і x20 точки локальної ринкової рівноваги є функціями цін p0 , p1, p2 , тобто:

x0	D	p	0	, p , p	2	,	x	0	D	2	p	0	, p , p	2		(1.13).
1	1			1				2					1

Вирази (1.13) називаються функціями попиту на ресурси

(витрати). Їх значення x10 і x20 виражають оптимальні вибори витрат (використання) ресурсів як функції ціни продукції, що випускається, і цін на ресурси.

Підставимо функції (1.13) у виробничу функцію y f x1,x2 , одержимо вираз:

y0 f D1 p0, p1, p2 , D2 p0, p1, p2 S p0, p1, p2 ,

який називається функцією пропозиції випуску.

У випадку короткострокового проміжку розглянемо конкретний приклад, коли другий ресурс x2 фірма може використовувати тільки в

заданому обсязі x2 0. Тоді задача максимізації прибутку перетворюється в задачу максимізації функції однієї змінної:

F x1, x2 p0 f x1, x2 p1x1 p2 x2 .

19

Можна

показати,

що

в

точці локальної

ринкової рівноваги

(x*

,x*) у випадку короткострокового періоду відповідні ізокванта та

1

2

ізокоста перетинаються, але не є дотичними.

і є функція

У розглянутому випадку

x

x x

, p

0

, p , p

2

1

1

2

1

попиту на перший ресурс при фіксованому обсязі x2

другого ресурсу.

Функція пропозиції випуску має вигляд

y f x1 x2 ,

p0, p1, p2 ,x2 .

Розглянемо випадок, коли процес виробництва описується за

допомогою однофакторної

виробничої функції

y f (X), де

X -

обсяг

використовуваних

ресурсів,

y

-

обсяг

продукції,

що

випускається. Проаналізуємо залежність прибутку фірми від обсягу

виробленої нею продукції :

F y p y C y .

Похідні від функцій витрат, доходу і прибутку називаються

граничними функціями: C'(y) - це гранична функція витрат

виробництва, R'(y) гранична функція доходу і F'(y) - гранична

функція прибутку. Економічна інтерпретація граничної функції витрат

така: так як похідна C'(a) за означенням, миттєва швидкість зміни

витрат

при

y a,

то

C'(a)

являє

собою

наближено додаткову

вартість виготовлення ще одного виробу. Іншими словами, C'(a) -

додаткові витрати при виготовленні (a 1) виробу. Аналогічно, R'(a) -

додатковий дохід і F'(a) - додатковий прибуток, отриманий від

реалізації (a 1)-го виробу.

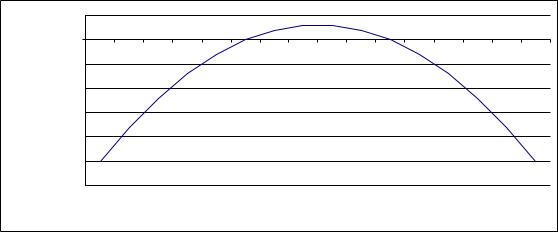
На рис.1.4 показано типову функцію прибутку F. Відзначимо,

що максимальний прибуток досягається, якщо обсяг проданих виробів

y a,

тому що в цій точці дотична до кривої F(y)

горизонтальна, її

кут із віссю Oy дорівнює нулю, і отже, ми маємо F'(a) 0.

100000F(y)

0

0

100

200

300

400

500

600

700

800

900

1000 1100 1200 1300 1400 1500

-100000

-200000

-300000

-400000

-500000

-600000

y

Рис. 1.4

20