Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах

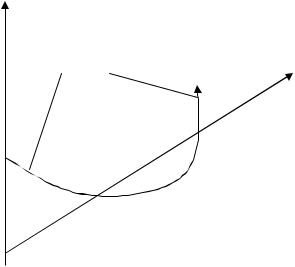
Оскільки F(y) R(y) C(y), то	F'(a) R'(a) C'(a) і
значить:
R (a)=C (a)	(1.14).
Таким чином, для максимального	прибутку y виконується
рівність:
R (y)=C (y) ,	(1.15)

або, мовою економіки, максимальний прибуток досягається якщо граничний дохід дорівнює граничній вартості.

Розглянемо приклад. Нехай функції витрат і доходу деякої фірми відповідно мають вигляд:

	C(y) y2	500000 і		R(y) 1500y.
Тоді прибуток фірми:
	F ( y) R( y) C ( y) y 2			1500 y 500000
або	F(y) (y 500)(y 1000).
Прирівнюючи F(y) 0			і розв’язуючи отримане рівняння
відносно	y, отримаємо:	y 500 і		y 1000. Виходить, точки
перетину кривої F(y) з віссю			y 500	виробів і y 1000 виробів. На

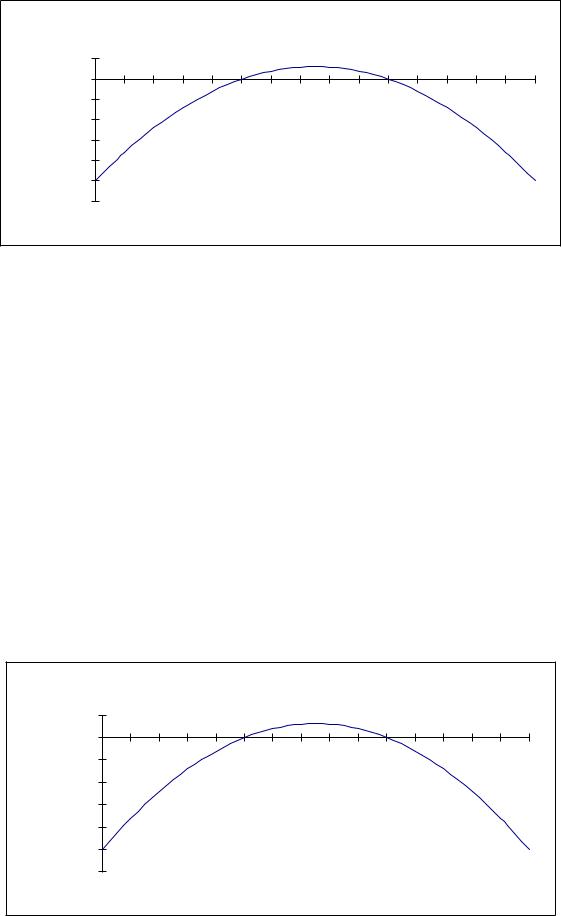
рис.1.5 і 1.6 показано графіки функцій C, R і F. Видно, що фірма дістане прибуток, якщо виробить і реалізує від 500 до 1000 виробів, і зазнає збитків, якщо виробить і реалізує менше 500 або більше 1000 виробів.

C

Збиток

R(y)=1500y

Приріст

y 500 1000

Рис. 1.5

21

	100000							Приріст
	0
	-1000000	100	200	300	400	500	600	700	800	900	1000	1100	1200	1300	1400	1500
	-200000
	-300000														F(y)
	-400000
	-500000
	-600000
									y
								Рис. 1.6

Граничні функції вартості, доходу і прибутку в даному прикладі

визначаються	відповідно:		C'(y) 2y,		R'(y) 1500	і
F'(y) 2y 1500.		Підставивши у		функцію	C'(y) значення
y 600, отримаємо		C'(600) 1200.		Це означає, що виготовлення

601 виробу коштуватиме фірмі наближено у 1200 умовних грошових одиниць (у.г.о.). Відповідно, для функції доходу R'(600) 1500, дохід від продажу 601 виробу буде 1500 у.г.о. Наближений додатковий прибуток становить F'(600) 300 у.г.о.

Прибуток фірми буде максимальним, якщо R'(y) C'(y). Прирівнявши відповідні похідні функцій, отримаємо рівняння: 1500 2y. Звідки знаходимо: y 750. Тобто, фірма отримає максимальний прибуток, якщо вона виробить і реалізує 750 одиниць продукції. За таких умов фірма отримає максимальний прибуток:

F(750) 62500 у.г.о. (рис. 1.7).

	100000
	0															y
	-1000000
		100	200	300	400	500	600	700	800	900	1000	1100	1200	1300	1400	1500
	-200000
	-300000														F(y)
	-400000
	-500000
	-600000

Рис. 1.7

22

Розглянемо випадок, коли фірма ще не встановила ціну на товар. Ціна для отримання прибутку встановлюється залежно від попиту: якщо попит високий, то фірма може продати велику кількість товарів за низькою ціною і, навпаки, при низькому попиті фірма буде вимушена збільшувати ціну товару для отримання даного доходу.

Витрати C на виробництво продукції є монотонно зростаючою функцією обсягу виробництва C C(y), C'(y) 0. Дохід фірми R

обчислюється як добуток обсягів продажу y* на ціну реалізованої продукції p0: R p0 y*. Вираз для прибутку має вигляд:

F R C p0y* C(y).

Обсяг продажу визначається попитом D і пропозицією S:

y* min{D,S}.

Розглянемо умови зростання прибутку F внаслідок зміни p0 і y.

ПриD y прибуток F дорівнює:

F p0y C(y).

Функція прибутку зростає із зростанням ціни p0 (оскільки

F y 0). Отже зростання ціни збільшує прибуток доти, доки цей

p0

вираз має місце для прибутку, тобто, до рівності попиту та пропозиції. При D y має місце наступна рівність:

F p0D(p0) C(y).

	F	Витрати C(y)	збільшуються	зі	зростанням y. Оскільки
		C'(y) 0, то,	при сталій	ціні	і при зменшенні обсягу
	y

виробництва, прибуток залишається незмінним, витрати зменшуються і прибуток зростає.

Отримано важливий результат: оптимальний (максимальний) прибуток відповідає рівності попиту та пропозиції, тобто оптимальні значення ціни і обсягу виробництва необхідно шукати на кривій рівноваги y D(p).

1.3. Визначення бар’єрних показників у фінансово-економічному аналізі

У практиці фінансово-економічного аналізу досить часто виникає необхідність визначати бар’єрні (порогові, гранично допустимі) значення деякого параметра. Під бар’єрним значенням

23

параметра розуміють таку його величину, перевищення якої призводе до позитивного, або, навпаки, негативного кінцевого результату у рамках деякої виробничої або фінансової системи. Наприклад, якщо мова йде про визначення обсягу виробництва якого-небудь виду продукції, то бар’єрним його значенням є такий обсяг випуску, при якому отриманий прибуток дорівнює нулю. Перевищення цього обсягу дає прибуток, виробництво в меншому обсязі є збитковим. Таке та багато інших завдань вирішуються за допомогою методу бар’єрної або критичної точки (break-even point). Метод бар’єрної точки широко використовується у фінансовому проектуванні, при розробці бізнес-планів і при вирішенні різноманітних проблем: при визначенні бар’єрного значення процентної ставки, ціни товару, терміну виконання фінансової операції і т. ін.

Найбільш проста постановка завдання здійснюється за допомогою лінійної моделі. У випадках, коли процес формування витрат або ціни продукції описується нелінійними функціями, застосовують нелінійні моделі. Вид і параметри таких кривих можуть бути встановлені, наприклад, у ході статистичного аналізу, або їх можна задати експертно. Якщо усі вихідні дані встановлені однозначно, отримують тільки одне розрахункове значення випуску. За умови неоднозначності постійних або змінних витрат отримують діапазони бар’єрних показників випуску.

Треба зауважити, що деякі проблеми визначення бар’єрних точок, зокрема визначення бар’єрних точок для податкових ставок і бар’єрних точок в умовах невизначеності, ще й досі обговорюються у фінансовій літературі.

До недавнього часу метод бар’єрної точки застосовувався тільки у статиці. Економічні показники розглядались у рамках одного, порівняно короткого періоду. В останній час цей метод розповсюджується і на потоки платежів, що охоплюють ряд послідовних часових інтервалів. У цих випадках за допомогою дисконтування можливо врахувати важливіший фактор – час (а саме, терміни інвестування і терміни віддачі від інвестицій). Так постановку задачі з визначення бар’єрного випуску продукції можна розширити, враховуючи додаткові умови. Поточні витрати і надходження від реалізації продукції можна подати у вигляді потоків платежів. Тут можливі два конкуруючі підходи до визначення бар’єрного випуску.

Упершому, який умовно назвемо бухгалтерським, інвестиції не беруться до уваги безпосередньо – вони враховуються через амортизаційні відрахування. Останні включають до поточних витрат.

Удругому, фінансовому, підході інвестиції відіграють ключову роль – вони виступають у якості самостійного фактора.

24

Питання до самоконтролю

1.Що являє собою граничний аналіз в економіці?

2.Застосування поняття еластичності в економіці. Наведіть приклади.

3.Модель збору податків, що базується на концепції попиту та пропозиції.

4.Виробнича функція та технологічна результативність виробництва. Наведіть приклад.

5.Сутність ефективної та неефективної областей ізокванти.

6.Підходи щодо визначення функції витрат у короткотерміновому та довготерміновому періодах. Наведіть приклади.

7.Сутність ізокост постійних витрат. Наведіть приклад.

8.Сутність реакції виробника на зміну цін ресурсів.

9.Поясніть, у чому полягає сутність реакції виробника на одночасну зміну ціни випуску та цін ресурсів.

10.Лінійна модель для визначення бар’єрної точки.

11.Нелінійні моделі для визначення бар’єрної точки.

12.Наведіть приклади застосування бар’єрних показників у фінансовому аналізі.

13.Визначення бар’єрної точки за умови невизначеності вихідних даних.

14.Бухгалтерський та фінансовий підходи до визначення бар’єрної точки.

Рекомендована література: [1], [9], [25], [51].

25

РОЗДІЛ 2 ДОСЛІДЖЕННЯ МОДЕЛЕЙ ОПТИМІЗАЦІЇ ФІНАНСОВОЇ

ДІЯЛЬНОСТІ ПІДПРИЄМСТВА ЗА ДОПОМОГОЮ МЕТОДІВ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ

2.1. Виробнича задача лінійного програмування

Мета вивчення теми – набуття студентами навичок застосування методів математичного програмування у дослідженні фінансової діяльності підприємства при прийнятті управлінських рішень у майбутній фаховій діяльності.

Вивчення теми базується на знаннях, отриманих студентами з дисципліни „Математичне програмування”.

Математичне програмування – це розділ прикладної математики, предметом якого є задачі на знаходження екстремуму деякої функції за заданих певних умов.

Розрізняють два види задач: детерміновані і стохастичні. Детерміновані задачі не містять випадкових змінних чи параметрів. У стохастичних задачах використовується інформація, яка містить елементи невизначеності. Об’єктами математичного моделювання можуть бути різноманітні галузі людської діяльності, в тому числі: економіка, фінанси, транспортна галузь, військова справа та інше. З метою вибору найкращого варіанта дій в тій чи іншій ситуації необхідно знайти екстремум деякої функції, яку називають цільовою, за деяких обмежень на змінні математичної моделі. Ці змінні можуть бути дискретними або неперервними. Сама цільова функція та обмеження, в свою чергу, поділяються на лінійні і нелінійні.

Залежно від математичних властивостей оптимізаційних задач математичного програмування розроблено різні методи їх розв’язування. Найбільш відомими є методи лінійного програмування, коли розглядаються детерміновані, неперервні процеси, а цільова функція і всі обмеження є лінійними. Лінійне програмування –це метод математичного моделювання розроблений для оптимізації використання обмежених ресурсів.

Розглянемо постановки типових виробничих задач лінійного програмування.

Задача про використання ресурсів (задача планування виробництва).

Нехай підприємство має m видів ресурсів Si у кількості bi i 1,2,...,m одиниць, з яких виробляється n видів продукції Pj.

Для виробництва одиниці j-го вигляду продукції витрачається aij

26

одиниць i-го виду ресурсу, а вартість вказаної одиниці продукції складає сj грошових одиниць. Потрібно так спланувати

виробництво, щоб загальний прибуток від реалізації продукції був максимальним.

Позначимо через xj j 1, 2,..., п				кількість одиниць j -го
виду продукції, запланованої для виробництва. Тоді						задачу лінійного
програмування можна сформулювати так:
Знайти максимальне значення лінійної функції загального
прибутку:
z = с1 x1+с2 x2+…+с n					xn	(2.1)
за умов виконання обмежень:
a11x1 a12x2	...	a1nxn			b1 ,
a21x1 a22x2	...	a2nxn			b2 ,
..................................................						(2.2)
am1x1 am2x2 ...		amnxn				bm .
x1 0, x2	0,	...	xn	0.		(2.3)

Математична модель виробничої задачі (2.1) - (2.3) або її варіанти широко застосовується для розв’язування різних економічних задач, де виникають проблеми досягнення максимального прибутку або мінімізації собівартості тієї чи іншої виробничої діяльності при обмежених ресурсах.

Транспортна задача

Загальна постановка транспортної задачі полягає у визначені такого плану перевезень деякого однорідного вантажу з m пунктів відправлення A1, A2,....Am у n пунктів призначення B1,B2,....Bnщо

забезпечує мінімальну вартість перевезень усього вантажу, або мінімальний час його доставки. Розглянемо математичну модель для

першого варіанта задачі оптимальності. Позначимо через cij

мінімальні тарифи перевезення		одиниці		вантажу з і-того пункту
відправлення у j-й пункт	призначення,			через	ai запаси	вантажу
у і-му пункті відправлення,	через bj		потреби у вантажі у j-тому
пункті призначення, через		хij	кількість		одиниць	вантажу,

27

перевезеного з і-того пункту відправлення у j- й пункт призначення. Тоді математична постановка задачі полягає у визначенні мінімального значення функції вартості перевезень:

m

n

f

cijxij

, за умов

i 1

j 1

m

xij

bj

j 1, 2,

,

n ,

i 1

n

xij ai

i 1, 2,

,

m ,

j 1

xij

0

i 1,

2,... ,m ,

j 1,

2,

,

n (2.4)

хij (i

;

j

)

Оскільки

змінні

1, m

1, n

задовольняють

системам лінійних рівнянь і умовам невід’ємності (2.4), то виконання цих умов означає що забезпечується доставка необхідної кількості вантажу у кожний з пунктів призначення, вивіз наявного вантажу з усіх пунктів відправлення, а також виключаються зворотні перевезення.

Задача про раціон

Раціон годівлі сільськогосподарських тварин може включати кілька видів кормів: сіно, силос, концентрати і т. ін. – у різних

пропорціях. Нехай	у щоденному раціоні повинно бути m видів
поживних речовин	Si i 1,2,...,m у кількості не менш ніж bi

(i=1,2,…,m) одиниць і повинно бути використано n видів кормів

Pi i 1,2,...,n . Для складання математичної моделі задачі позначимо через aij (i=1,2,…,m; j=1,2,…, n) кількість одиниць i-го виду поживної речовини, що міститься в одиниці j-го виду корму, а через сj позначимо вартість одиниці j-го виду корму. Нехай xj – запланована кількість одиниць j-го виду корму в денному раціоні.

Представимо початкові дані задачі у наступному вигляді

(табл. 2.1):

28

Таблиця 2.1

		Мінімальна	Кількість одиниць i-го виду поживної
			речовини, що містяться в одиниці j-го
	Поживні	добова норма
				виду корму
	речовини	поживної
			P1	P2			Pn
		речовини
	S1	b1	a11	a12			a1n
	S2	b2	a21	a22			a2n
	Sm	bm	am1	am2			amn
	Вартість
	одиниці j-го виду		с1	с2			сn
	корму

Необхідно знайти найекономніший раціон годівлі, тобто мінімальне значення лінійної функції:

f=c1x1+c2x2+…+cn xn

за умов

a11x1 a12x2 ...			a1nxn b1,
			a2nxn b2,
a21x1 a22x2 ...
................................................
a	x a	x ...	a	mn	x b ,
	m1 1	m2 2			n m
xj 0 j 1,			2, ...,		n .

Аналогічно можна сформулювати і задачу про дієту, яка задовольняла б потреби людини в поживних речовинах і вимагала б найменших затрат.

Задача раціональної кредитної політики банку

Комерційний банк АВС має можливість сформувати портфель кредитів об’єму s. Представимо можливі типи банківських кредитів у наступному вигляді (табл. 2.2):

29

				Таблиця 2.2
Тип кредиту			Ставка	Імовірність
			проценту	безнадійних боргів
Кредити фізичним особам			c1	р1
Кредити	на	придбання	c2	р2
автомобілів
Кредити на придбання житла			c3	р3
Сільськогосподарські			c4	р4
Комерційні			с5	р5

Безнадійні борги будемо вважати такими, що не повертаються, тому вони повинні відніматися від можливих доходів. Конкурентна боротьба з іншими фінансовими установами заставляє банк не менш ніж процентів від загальної суми кредитів направляти на сільськогосподарські та комерційні кредити. Для підтримки політики місцевої влади щодо розбудови житла для населення банк планує

вкласти в кредити на придбання житла не менш ніж процентів від загальної суми кредитів на придбання автомобілів, фізичним особам і на придбання житла.

						Таблиця 2.3
	Тип	Кредити	Кредити	Кредити	Сільсько-
		фізичним	на	на	господар-	Комерційні
	кредиту		придбання	придбання
		особам	автомобілів	житла	cькі
	Позначення	х1	х2	х3	х4	х5
	змінної

Банк також повинен виконувати розпорядження національного банку щодо того, що відношення безнадійних боргів до загальної суми кредиту не повинно перевищувати . При цьому вводимо ще одне припущення, що всі кредити банку виділяються наближено одночасно. Це дозволяє не враховувати фактор часу при дослідженні задачі. Змінні для фінансово-економічної моделі визначені в табл. 2.3. Завданням банку АВС звичайно є максимізувати чистий прибуток. Виходячи з цього цільову функцію запишемо наступним чином. Знайти максимум функції

z = c1 (1- р1)x1+c2 (1- р2)x2+ c3 (1- р3)x3 + c4 (1- р4)x4 + c5 (1- р5)x5 -

- р1x1 - р2x2 - р3x3 - р4x4 - р5x5

за умов:

30