Математичні моделі у фінансах / Рядно О.А. та ін. Математичні моделі у фінансах

розрахуйте кількісні оцінки ризику операційної діяльності малих підприємств та усіх підприємств області; проаналізуйте їх та зробіть порівняльний аналіз;

розрахуйте кількісні оцінки ризику операційної діяльності малих підприємств області різних видів економічної діяльності; проаналізуйте їх та зробіть порівняльний аналіз;

оцініть систематичний ризик операційної діяльності малих підприємств різних видів економічної діяльності по відношенню до малих підприємств у цілому, зробіть висновки;

Питання до самоконтролю

1.Назвіть показники, що застосовуються у фінансовому менеджменті для кількісного вимірювання величини ризику.

2.Наведіть приклади показників ступеня ризику у відносному вираженні.

3.Чому і в яких випадках для оцінювання переваг одного з кількох варіантів проектів використовують коефіцієнт варіації?

4.У яких випадках доцільно оцінювати ризик за допомогою коефіцієнта семіваріації?

5.У яких ситуаціях ризик доцільно оцінювати за допомогою коефіцієнта асиметрії?

6.У яких ситуаціях ризик доцільно оцінювати за допомогою коефіцієнта ексцесу?

7.Поясніть, що означають терміни: „допустимий”, „критичний” „катастрофічний” ризик, наведіть приклади кількісного визначення цих величин.

8.Наведіть основні правила та побудуйте гіпотетичну криву ймовірностей збитків у фінансовому підприємництві.

9.Сутність різних способів щодо визначення структури резервів на покриття ймовірних затрат (збитків).

10.Як можна визначити обсяг мінімального запасу сировини?

11.Сутність методів визначення ступеня ризику щодо потреб у

запасах.

12.Сутність моделі М. Міллера і Д. Орра.

13.Сутність поняття „оптимальний резерв”.

14.Сутність імовірнісної моделі визначення оптимальних запасів із урахуванням ризику.

15.Альтернативні підходи у моделюванні оцінювання ринкової вартості підприємств. Наведіть приклади.

16.Посніть сутність банківської виробничої функції. Наведіть

приклад.

17.Концепція ринкової рівноваги для банківської сфери.

18.Поясніть сутність моделі динаміки фінансового стану банку.

19.Сутність методики прогнозування динаміки фінансових ресурсів комерційного банку.

20.Основні концептуальні засади моніторингу стохастичної динаміки фінансового ресурсу комерційного банку.

Рекомендована література: [1], [5], [6], [20], [37], [45], [49].

71

РОЗДІЛ 4 РЕГРЕСІЙНІ МОДЕЛІ ФІНАНСОВОЇ ДІЯЛЬНОСТІ

ПІДПРИЄМСТВА ТА ФІНАНСІВ НА РЕГІОНАЛЬНОМУ І ДЕРЖАВНОМУ РІВНІ

4.1. Загальна лінійна економетрична модель

Мета вивчення теми – набуття студентами навичок застосування економетричних моделей у дослідженнях проблем фінансів при прийнятті управлінських рішень.

Вивчення теми базується на знаннях, отриманих студентами з дисципліни „Економетрія”.

Під економетричною моделлю розуміють рівняння регресії, побудоване на основі даних спостережень, яке встановлює залежність між економічними показниками. Проблема вивчення взаємозв’язків економічних показників є однією з найважливіших проблем економічного аналізу. Кожна економічна політика полягає в регулюванні економічних змінних, тому вона повинна ґрунтуватися на глибокому розумінні того, як ці змінні впливають одна на одну.

Основні етапи побудови загальної лінійної моделі такі:

1. Збір статистичних даних. Для побудови економетричної моделі, перш за все, треба зібрати статистичні дані. Джерелом статистичних даних можуть бути безпосередньо спостереження, документи, статистичні збірники, наукові та науково-практичні періодичні видання. Зібрані статистичні дані зручно розташувати у вигляді таблиці. Наприклад, якщо досліджується залежність економічного показника Y від деякого фактора X, і в нас є дані n спостережень, то ми їх можемо записати у вигляді табл. 4.1.

						Таблиця 4.1
	Дані спостережень за показником Y і фактором X
i	1	2	3	…	i	…	n
y	y1	y2	y3	…	yi	…	yn
x	x1	x2	x3	…	xi	…	xn

Статистична база для економетричних моделей може складатися як із часових, так і з просторових статистичних рядів даних.

Часовим (динамічним) рядом називається статистичний ряд, в якому значення показника yi (i=1,n) і фактора xi (i=1,n) упорядковані в часі. Якщо дані спостережень вимірюються в грошових одиницях, вони мають бути наведені до одного періоду часу.

Просторові (структурні) ряди даних являють собою послідовність значень показника Y і фактора X у різних економічних сукупностях. Просторові ряди, на відміну від динамічних, дають

72

можливість вивчати не розвиток процесу в динаміці, а кількісний (структурний) вклад фактора X у показник Y.

2. Попередній аналіз даних

2.1. Побудова діаграми розсіювання. Попередній аналіз даних у випадку, коли вивчається залежність між двома змінними, починається з побудови діаграми розсіювання. Для цього дані спостережень yi над показником Y і – xi над фактором X, які розглядаються як координати точок (xi, yi), відкладають на

координатній площині XY.

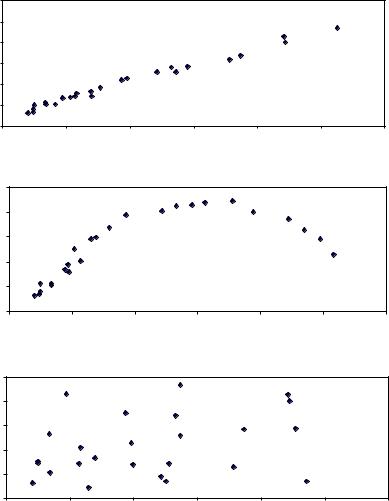
Аналіз розташування точок на діаграмі розсіювання дозволяє зробити попередній висновок про характер зв’язку між змінними X і Y. На рис. 4.1 зображено три ситуації:

-на графіку (а) взаємозв’язок між X і Y близький до лінійного;

-на графіку (б) взаємозв’язок між X і Y описується нелінійною функцією;

-на графіку (в) явний взаємозв’язок між X і Y відсутній.

2.2. Обчислення числових характеристик показника Y і фактора X.

Числові характеристики обчислюються за такими формулами:

n

n

yi

xi

y

i 1

,

x

i 1

– середні значення відповідно показника

n

n

Y і фактора X,

n

n

(yi

y

)2

(xi

x

)2

D[Y]

i 1

,

D[X]

i 1

– дисперсії

n

n

відповідно показника Y і фактора X,

[Y]

[X]

D[Y]

,

D[X]

– середньоквадратичні

відхилення відповідно показника Y і фактора X,

n

(xi

x

)(yi

y

)

K[X,Y]

i 1

–

статистичний

кореляційний

n

момент між X і Y.

73

1200

Y

1000

800

600

400

200

0

0

100

200

300

400

500

600X

а)

1000

Y

800

600

400

200

0

0

100

200

300

400

500

600X

б)

1000

Y

800

600

400

200

0

0

100

200

300

400

500

600X

в)

Рис. 4.1 Різні види діаграм розсіювання

2.3. Обчислення парного коефіцієнта кореляції.

Вибірковий коефіцієнт кореляції змінних X і Y обчислюється за формулою:

r[X,Y]	K[X,Y]	.	(4.1)
[X] [Y]

Коефіцієнт кореляції характеризує ступінь щільності лінійної залежності між випадковими величинами X, Y і змінюється в межах від –1 до 1, причому, коли r[X,Y] 0, то між випадковими величинами X і Y існує додатна залежність ( тобто якщо зростає чинник X, то відповідно зростає показник Y, так само, якщо спадає чинник X, то спадає і показник Y); коли r[X,Y] 0, то між величинами X і Y існує від’ємна залежність (якщо чинник X зростає, то показник Y спадає, і якщо чинник X спадає, то показник Y зростає).

74

Близьке до нуля значення коефіцієнта кореляції свідчить про відсутність лінійного зв’язку між змінними X та Y. У випадку абсолютної лінійної залежності коефіцієнт кореляції дорівнює r[X,Y] 1 (додатний лінійній зв’язок) або r[X,Y] 1 (від’ємний лінійний зв’язок). Якщо значення коефіцієнта кореляції по модулю наближається до 1, то між X і Y існує міцний лінійний зв’язок.

3. Побудова лінійної моделі регресії. Якщо за допомогою коефіцієнта кореляції встановлено наявність статистичного лінійного зв’язку між показником Y та фактором X, наступним етапом дослідження є побудова лінійної моделі регресії:

	yi a0 a1xi li,	(4.2)
де	a0,a1 – невідомі параметри регресії, що мають бути оцінені;
	li – відхилення даних спостережень показника	yi від

розрахункових значень показника yi, які знаходяться за формулою:

yi a0 a1xi.

(4.3)

Оцінки параметрів a0,a1, знайдені за допомогою методу найменших квадратів, можна записати в такому вигляді:

a		K[X,Y]	,
				(4.4)
1		D[X]

a0 y a1x.

Отримане значення оцінки параметра a1 означає, що при зміні фактора X на одиницю показник Y зміниться на a1 одиниць.

Зазначимо, що коли значення коефіцієнта кореляції прямує до нуля, це говорить про відсутність лише лінійного зв’язку між змінними, але не про відсутність зв’язку між ними взагалі. У цьому випадку можна спробувати розглянути нелінійний зв’язок між X і Y. Найчастіше використовуються в макрота мікроекономічних дослідженнях такі криві:

експоненційна:	y	a	a xi	;
	i		0 1
степенева (мультиплікативна):	y	a	x a1	;
	i		0 i

75

1

зворотна:

yi

a0

a1

;

x

i

квадратична:

y

a

0

a x

a

x 2

;

i

1 i

2 i

модифікована експонента:

y

a

0

a xi

a

2

;

i

1

крива Гомперця:

x

i a2 ;

логістична крива:

yi ea0a1

1

yi

.

a

0

a xi

a

2

1

Методи оцінки параметрів нелінійних моделей регресії докладно розглянуто у підручнику [19].

Якщо на економічний показник Y суттєво впливають декілька факторів X1, X2,..., Xm, у цьому випадку можна розглянути модель

множинної лінійної регресії:
yi a0 a1x1i a2x2i ... amxmi		li.	(4.5)
Для знаходження точкових оцінок параметрів регресії
застосовують формулу:
1	X T Y ,		(4.6)
A X T X

	a0
	a
де A		1
	a	2	,
	...
	am

y1
y2
.
Y	,
yi
.
yn

1		x11	x21 ...				xm1
	1	x	x	22		...	x	m2
		12
... ...			... ...				...
X	1	x	x		2i	...	x		mi	.
		1i
... ...			... ...				...
	1	x1n	x2n ...
							xmn

Перший стовпець регресійної матриці [Х] складається з одиниць, другий та інші дорівнюють значенням факторів

x1i, x2i,...,xmi.

Розрахункові значення показника знаходяться за формулою:

yi a0 a1x1i a2x2i ... amxmi.

(4.7)

76

4. Перевірка загальної якості рівняння регресії. Побудова економетричної моделі – це довгий та складний процес, і як правило, перше рівняння, що отримано, дуже рідко є задовільним в усіх відношеннях. Тому після того, як знайдені оцінки параметрів a0,a1

рівняння (4.2) (або оцінки a0,a1,a2,...,am рівняння (4.5)), треба проаналізувати якість залежності, яку оцінено.

4.1. Оцінка дисперсії відхилень.

Попереду необхідно за формулою (4.3) або (4.7) обчислити

розрахункові значення yˆi (i 1,n)		показника Y та визначити
відхилення li:
li yi yi.		(4.8)
Оцінку дисперсії відхилень s2 знаходять таким чином:
	n
s2	li2	(4.9)
	i 1	,

n m 1

де m – кількість факторів, що розглядаються у моделі.

4.2. Стандартна помилка регресії.

Якість оцінки середньої величини показника Y характеризує середньоквадратична (стандартна) помилка регресії s, яка є мірилом розкиду фактичних значень yi показника регресії:

		n
		li2		(4.10)
	s	i 1		.
		n m 1

Стандартна помилка регресії s є розмірною величиною і подає абсолютне стандартне відхилення фактичних значень показника відносно регресії. Аби мати уявлення про масштаб цієї помилки, її можна віднести до середнього значення показника:

s		s	100%.	(4.11)
		y

4.3. Коефіцієнт детермінації. Іншим показником якості регресії є коефіцієнт детермінації. Він показує, яку частку від загальної варіації показника становить детермінована складова, що її виявляє і враховує регресія, або яку частку варіації вона пояснює.

Вибірковий коефіцієнт детермінації R2 знаходиться за формулою:

77

			(y		y	)	2
	R2		i					.	(4.12)
			(yi		y	)	2

Для парної лінійної регресії коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції:

R2=r2[X,Y].

(4.13)

Коефіцієнт детермінації змінюється в межах від 0 до 1. Чим більше спостережувані значення показника наближаються до лінії

регресії, тим ближче значення R2 до одиниці. Ситуація, коли R2=1, означає переростання статистичної залежності у функціональну,

детерміновану. Випадок R2=0 свідчить про відсутність будь-якого зв’язку між показником і фактором.

4.4. Перевірка адекватності моделі за допомогою F-критерію Фішера.

Перевірка моделі на відповідність даним спостережень за F- критерієм Фішера передбачає здійснення наступних етапів:

1) обчислюється розрахункове значення F критерію Фішера:

	R2		n m 1
Fp 1 R2			m	;			(4.14)
2) для обраного рівня значимості						(P=1– – надійна
ймовірність) і числа ступенів		свободи		k1 m,			k2 n m 1 за

таблицею F-розподілу знаходиться табличне значення FP;k1;k2 ;

3) отримане розрахункове значення порівнюється з табличним. При цьому, якщо Fp FP;k1;k2, то з надійністю P можна вважати,

що розглянута математична модель адекватна даним спостережень, у протилежному випадку з надійністю P розглянуту парну регресію не можна вважати адекватною.

5. Перевірка статистичної значимості коефіцієнтів рівняння регресії. Знайдені за даними спостережень значення параметрів регресії являють собою статистичні оцінки цих параметрів, одержані на основі обмеженої інформації. Через обмеженість вибіркових даних можливі ситуації, коли істинне значення параметра дорівнює нулю, тоді як розраховане внаслідок випадкових коливань даних, на базі

78

яких його обчислено, відмінне від нуля. Відтак виникає потреба у перевірці статистичної значущості параметрів регресії. Це можна

зробити за допомогою аналізу відношення tpj ( j 1,m) коефіцієнта регресії aj до свого стандартного відхилення Saj:

	t	pj		aj	,	(4.15)
				Saj

яке має t-розподіл Стьюдента з n-m-1 ступенями свободи. Формули для оцінки Saj такі:

Saj Saj2 ,

(4.16)

де Saj2 – оцінки дисперсій параметрів регресії, які знаходяться з коваріаційної матриці для параметрів aj :

Sa20

Sa0a1

Sa0a2 ...

Sa0am

Sa21

Sa1a2 ...

Sa1am

Sa1a0

1

S

S

S2

...

S

a2a0

a2a1

s2 X T X .

a2

...

a2am

...

...

...

...

Sama1

Sama2 ...

2

Sama0

Sam

У випадку парної лінійної регресії:

Sa1

s2

s2

;

n

nD[X]

(xi

x

)2

i 1

n

n

s2 xi2

s2 xi2

Sa0

i 1

i 1

.

n

n2D[X]

n (xi

x

)2

i 1

(4.17)

(4.18)

(4.19)

79

Для обраного рівня значимості (P=1– – надійна ймовірність)

і числа ступенів свободи	k n m 1	в таблиці		t-розподілу
знаходять табличне значення t-статистики tP,k . Якщо			tpi	tP;k то з
надійністю P заперечується	гіпотеза, що	коефіцієнт		aj може

дорівнювати нулю, оцінку параметра aj можна вважати значимою.

6. Прогнозування за допомогою регресійної моделі. Модель,

яка побудована на основі даних спостережень, що вже є в наявності, може використовуватись для прогнозу значень залежної змінної Y в майбутньому або для інших значень незалежної змінної. Прогноз показника дістають підстановкою у здобуте регресійне рівняння (4.3) значення фактора xp, для якого бажають отримати прогноз, або, для

множинної лінійної регресії, підстановкою у рівняння (4.7) значень факторів x1p, x2p,...,xmp .

Результатом є точкова оцінка середнього значення показника yp при заданих значеннях факторів.

Границі надійних інтервалів індивідуальних прогнозних значень показника знаходять наступними чином:

нижня границя: yp yp;

верхня границя: yˆ p yˆp,

де

yˆp tP,k Sy2ˆp , Sy2ˆp

– оцінка дисперсії індивідуального

прогнозного значення показника, яка має вигляд:

Sy2ˆ p	1	X p s2,
	s2 X p T X T X		(4.20)

X p T x1p, x2p,...,xmp .

У випадку парної лінійної регресії:

yˆp tP,k s 1	1		(xp	x	)2			.
			n
	n							(4.21)
			(xi			x	)2
			i 1

7. Обчислення коефіцієнтів еластичності. У випадку парної лінійної регресії для оцінки впливу на економічний показник Y фактора X без урахування одиниць виміру використовують коефіцієнт еластичності, який обчислюється за формулою:

80