12. Замечательные пределы.
1) lim f(x)sinx/x =1(при х→0) – первый замечательный предел.
Док-во. Т.к. ф-я y= sinx – четная, то достаточно показать, что предел при
х→0 справа равен 1
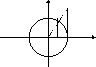
T
M
tgx
x
K A
O
MK= sinx Видно, что sinx<x<tgx,
1<x/ sinx<1/cosx
1>sinx/x>cosx
при х→0 справа имеем lim cosx=1, lim 1=1. Значит получили требуемое
равенство.
2) lim (1+1/x)x =e(х→+ (-)∞) – второй замечательный предел.
Док-во.
Докажем
1)при +∞.Пусть х – любое число. Найдем такое целое n, чтобы
выполнялось нер-во:
n ≤ x< n+1 (1)
Будем считать, что х>1,n>0. Сделав необходимые преобразования, получим:
1+1/ n ≥ 1+1/x> 1+1/(n+1)
Зная условие (1), можем получить: (1+1/ n)n+1≥
(1+1/x)x> (1+1/(n+1))nили f(x) ≥(1+1/x)
x>g(x). При х→+∞ ,n →+∞, f(x) и g(x)→е.
По св- ву предела ф-и lim (1+1/x)x→е(при х→+∞),
что и т.д.
2) при -∞. Пусть х=-t, где t>0.
(1+1/x)x=(1-1/t)-t =((t-1)/t)-t
=(t/(t-1))t =(1+1/(t-1))t =(1+1/(t-1))t-1
(1+1/(t-1))xВыражение в правой части →е*1=е при
х→-∞, т.е. t →+∞, что и т.д.
13. Формула непрерывных процентов.
К0-исходный капитал.
Р- номинальная процентная ставка.
к- число периодов начисления .
Пусть к=1, тогда К=К0*(1+р/100)
к=2, К=К0(1+р/2*100)2
. к=360, К=К0(1+р/360*100)360.,т.е. К=К0(1+р/к*100)к
→К0*ер/100при к →∞(это случай, если начисление
процентов производится в течение одного года). Когда начисление процентов
производится на протяжении нескольких лет – t, то, разделив промежуток [0;t] на
к равных периодов начисления процентов, получим (к→∞):
К0lim (1+рt/100*к)к= К0*ерt/100
К=К0*ерt/100-формула непрерывных процентов.
14 Непрерывность функции в точке.
y = f(x), x0Î D(f)
Функция f(x), определенная в некоторой окрестности точки х0,
называется непрерывной в этой точке, если предел функции в точке x
0существует и равен значению в этой точке: lim f(x) = f(x0)
y y = f(x) x » x0;
f(x) » f(x0)
F(x0) y
x0 x Δy
x - x0 = Δx
f(x) – f(x0) = Δy
x x0
Δx x
f(x) непрерывна в точке x0Û lim Δy = 0
ΔX®O
Свойства функций непрерывных в точке
1)Если f(x), g(x) – непрерывны в точке x0, то f(x) ± g(x); f(x)•
g(x); f(x)/g(x) (g(x) ≠ 0) – также непрерывны в точке x0.
Докажем, что F(x) = f(x)•g(x) непрерывна в точке x0
Дано: f(x) и g(x) – непрерывны в x0Û lim f(x) = f(x0); lim g(x) = g(x0)
X®Xo X®Xo
lim (f(x)•g(x)) = limf(x)•lim g(x) (по свойству предела функции) = f(x0
)•g(x0) (по
X®Xo X®Xo X®Xo
определению непрерывности) ® F(x) = f(x)•g(x) непрерывна в x0.
2)
f(x) – непрерывна
в точке x0, существует такая окрестность точки
f(x0) > 0 x0
, во всех точках которой f(x) > 0.
15. Основные элементарные функции:
1. Степенные функции: y = xa,
где а – любое постоянное число. Областью определения считается промежуток x >
0, но если, например, а–натуральное число, функция определена для всех х.
2. Показательная функция: y = ax,
где a > 0, a ≠1. Область определения – множество всех действительных чисел.
3. Логарифмическая функция: y = logax,
где a > 0, a ≠1. Область определения: x > 0.
4. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y =
ctg x.
Область определения для sin x и cos x – множество действительных чисел.
5. Обратные тригонометрические функции: y = arcsin x, y = arccos x, y
= arctgx.
Область определения x Î [-1; 1] для arcsin x и arccos x, множество
действительных чисел для arctg x.
Действия над функциями, которые считаются допустимыми:
1. все арифметические действия (f + g, f – g, f•g, f/g);
2. построение сложной функции.
Элементарными функцияминазываются такие, которые получаются из основных
с помощью допустимых действий.
Элементарные функции непрерывны в каждой точке своей области определения.