Конспект Математическое моделирование. Автор: профессор МГОТУ Вилисов В.Я

x2

ОДР

3 2 1

Оптимальное
решение	x1

Оптимальное решение: x1 = 470.6 кг., x2 = 329.4 кг., L = 437.64 руб.

▲

1.4.3. Транспортная задача (или задача планирования перевозок)

Рассмотрим случай перевозки однородного продукта.

транспортную задачу (ТЗ) представляют в виде графа или матрицы. Граф ТЗ представлен на рис.

		Пункты отправления	Пункты
		(ПО)	назначения (ПН)
		A1	B1
	Объѐмы			Объѐмы
	предложений	A2	B2	спроса
	(запасы)			(заявки)
		…	…

Am Bn

В матричном (или табличном) виде ТЗ представлена в табл.

	ПО\ПН	B1	B2	…	Bj	…	Bn	Запасы
									ai
	A1	c11	c12	…	c1j	…	c1n		a1
	A2	c21	c22	…	c2j	…	c2n		a2
	…	…	…	…	…	…	…		…
	Ai	ci1	ci2	…	cij	…	cin		ai
	…	…	…	…	…	…	…		…
	Am	cm1	cm2	…	cmj	…	cmn		am
	Заявки							m	n
		b1	b2	…	bj	…	bn	ai	b j
	bj
								i 1	j 1

Для транспортной сети матрица затрат на перевозку остаѐтся неизменной. Ситуация при всяком новом планировании перевозок отличается лишь объѐмами спроса и

предложения, т.е. коэффициентами ai m b j n следующих ограничений:

11

n

xij

ai

,

i 1, m

j 1

m

xij

b j

,

j 1, n

i 1

xij 0 ,

i 1, m ,

j 1, n

представляет собой матрицу значений переменных X

mn , а целевая

xij

Решение

x

функция имеет вид:

m

n

L(

) cij xij ,

x

i 1

j 1

где коэффициенты cij имеют смысл обобщѐнных транспортных расходов при перевозке

единицы груза из i-го пункта отправления в j-й пункт назначения. Критерий имеет вид:

			m	n
L(		) cij xij			min
	x
			i 1	j 1	x
ТЗ называется сбалансированной, если суммарный спрос равен суммарному
предложению:
m			n
ai			b j
i 1			j 1

Если ТЗ несбалансированна, то она превращается в сбалансированную добавлением фиктивного пункта отправления или пункта назначения.

ТЗ сводится к обычной ЗЛП, хотя существуют специальные методы еѐ решения.

Пример.

Дано. На двух складах предприятия имеется запас зерна, которое необходимо перевезти трѐм покупателям. Транспортная таблица имеет вид:

	Пок.1	Пок.2	Пок.3	Запасы
Склад 1	42 руб	55 руб	60 руб	50 т
Склад 2	36 руб	47 руб	51 руб	40 т
Заявки	20 т	36 т	34 т

Искомые решения можно представить как количество xij зерна, перевозимого со Склада i Покупателю j. Или в табличном виде:

	Пок.1	Пок.2	Пок.3	Запасы
Склад 1	x11 т	x12 т	x13 т	50 т
Склад 2	x21 т	x22 т	x23 т	40 т
Заявки	20 т	36 т	34 т

Приведѐм задачу к стандартной форме. Т.к. линейно независимы здесь лишь две переменные, то обозначим их как x и y , а остальные выразим через них:

	Пок.1	Пок.2	Пок.3	Запасы
Склад 1	x	y	50-x-y	50
Склад 2	20-x	36-y	x+y-16	40
Заявки	20	36	34

12

Поскольку все переменные должны быть неотрицательными, то можно записать следующие ограничения:

	x 0
	y 0
	50 x y 0
	20 x 0
	36 y 0
	x y 16
		0

	x 0
	y 0
или :	x y 50
	x 20
	y 36

x y 16

Подставив новые переменные в выражение ЦФ, и проведя необходимые преобразования, получим:

L(x, y) 45960 30x 10y

Оптимальное решение, полученное графическим методом будет следующим: x = 20, y = 30.

y

ОДР

x

▲

1.5. Анализ чувствительности решения ЗЛП к изменению исходных данных

Поскольку ОДР – многогранник, то в некоторых случаях малые изменения коэффициентов ЦФ (а значит и линий уровня ЦФ), могут приводить к переключению оптимального решения на другую крайнюю точку ОДР.

Переключение оптимального решения зависит и от других коэффициентов ЦФ.

На практике необходимость в анализе чувствительности решения ЗЛП возникает, например, в таких случаях:

текущие запасы на складе (правые части ограничений) известны с некоторой погрешностью и желательно знать, как ведѐт себя решение в пределах этой погрешности;

цены на продукцию варьируются в некотором диапазоне (например, при наличии скидок).

Рассмотрим влияние на устойчивость оптимальных решений:

изменения коэффициентов ЦФ;

правых частей ограничений.

Логика использования процедуры анализа чувствительности обычно имеет такой вид:

13

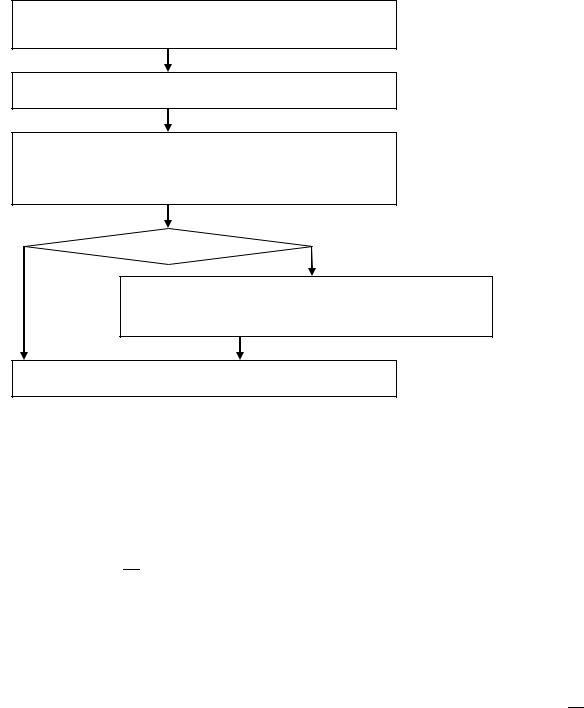
Выявление интервалов погрешности параметров ЗЛП

Вычисление оптимального решения ЗЛП

Анализ чувствительности решения ЗЛП и выявление множества решений, соответствующих интервалу погрешности

1

Кол-во решений

>1

Использование дополнительных ЦФ или предъявление вариантов решения ЛПР для выбора единственного решения

Реализация решения ЗЛП

1.5.1. Влияние коэффициентов ЦФ на решение ЗЛП

В реальной практике цены (т.е. коэффициенты ЦФ) могут отличаться для разных покупателей.

Т.к. на ориентацию линий уровня ЦФ влияют не абсолютные значения коэффициентов ЦФ, а лишь их отношения, то можно нормировать ЦФ, разделив все коэффициенты, например, на первый. Тогда для двух переменных получим:

L(x, y) 1x c2 y c1

Рассмотрим влияние коэффициентов ЦФ на примере задачи о производстве 2-х изделий, где активными являются 2-е и 3-е ограничения из 3-х, т.е. оптимальная точка образована пересечением линий:

3x1 + 0x2 = 460

1x1 + 4x2 = 420

Таким образом, здесь зона нечувствительности определяется диапазоном: 0 c2 4 . c1

14

x2

Зона изменчивости линий уровня целевой функции

Зона

нечувствительности опт. решения

Оптимальное

решение

ОДР

x1

x2

Варианты оптимальных решений с учетом зоны изменчивости

ОДР

x1

Если имеет место вариант, представленный на 2-ом рис., то возможны два кандидата на оптимальное решение. При этом для окончательного выбора необходимо привлечь дополнительные критерии либо передать оба варианта ЛПР для выбора одного из них по своему усмотрению.

1.5.2. Влияние правых частей ограничений на решение ЗЛП

Для задач производственного типа правые части имеют смысл распределяемых ресурсов (остатков на складе).

На практике обычно от момента решения задачи до момента реализации решения проходит некоторое время. За это время объем ресурсов может измениться. Поэтому важно знать запас устойчивости оптимального решений к изменению ресурсов.

Эту проблему ещѐ называют доступностью ресурсов.

Решения обладают запасом устойчивости лишь по тем ресурсам, ограничения которых не образуют оптимальную точку.

Изменение правой части приводит лишь к параллельному смещению линии ограничения, поэтому:

запас по данному ресурсу (или нечувствительность оптимального решения к уменьшению этого ресурса) определяется как величина, на которую надо сместить линию ограничения, чтобы она совпала с оптимальной точкой.

15

x2

Запас устойчивости по первому ресурсу

Оптимальное

решение

ОДР

x1

Численно запас устойчивости определяется как разность правой и левой (вычисленной) частей ограничения.

Так для первого ограничения в задаче сборки 2-х изделий в оптимальной точке

(x1=153.33 ; x2=66.67) получим:

x1 + 2x2 = 153.33 + 2*66.67 = 286.67 <= 430,

откуда запас равен 143.33.

2. Многокритериальная оптимизация

2.1. Скалярные и векторные критерии (показатели)

Скалярным называют критерий, построенный на основании одного показателя. Векторный критерий состоит из множества скалярных критериев, связанных логической

операцией И, например:

extr

(

) max L1

(

) min L2

(

) max Lm (

)

L

x

x

x

x

x

x

x

x

Выбор значений переменных, оптимальных по векторному критерию, называют

многокритериальной или векторной оптимизацией.

Для упрощения процедур оптимизации часто векторный критерий приводят к скалярному путѐм свѐртки целевых функций (ЦФ).

Рассмотрим варианты скалярного представления векторного критерия.

2.2. Метод главного (доминирующего) критерия

Все показатели и соответствующие им ЦФ ранжируют по степени их важности (например, экспертным методом). В итоге все ЦФ будут выстроены, например, так:

L2 (x) L1 (x) LK (x) .

Самый важный показатель выбирается в качестве единственного представителя вектора показателей, и дальнейшая оптимизация проводится по нему (см. рис. а)). ЦФ остальных критериев обычно переводятся в ограничения, тогда задача имеет, например, такой вид:

	opt arg max Li (			Lk (		) ak , k i
			) при		x
x		x
	x

16

Lk		L1	Lk		L1	Lk		L1
		L2			L2			L2
		L3			L3			L3
		L4			L4			L4
	а)	x		б)	x		в)	x

2.3. Метод гарантирующего (максиминного) критерия.

Эта свертка векторного критерия в скалярный основана на принципе гарантированного результата.

Пусть, например, все критерии на максимум.

Если критерии однородны (например, все в стоимостном исчислении) то в каждой точке ОДР следует выбрать тот из критериев, который доставляет соответствующей ему целевой функции минимальное значение. Тогда наилучшим будет то решение, которое обеспечит максимум среди всех минимальных значений (см. рис. б)):

xopt arg( max min Lk (x)) .

x k

Если критерии неоднородны, то предварительно все целевые функции нормируются, т.е. приводятся к единой безразмерной шкале. Для линейных критериев вида:

n

Lk (x) c jk x j

j 1

1-й вариант нормировки основан на следующем:

положение гиперплоскости в пространстве переменных не изменится от умножения/деления на положительное число;

положение гиперплоскости однозначно определяется нормальным (перпендикулярным) к ней вектором. Координатами этого вектора являются коэффициенты

ЦФ с jk .

Этот вариант нормировки приводит векторы ЦФ к единичной длине (нормальный вектор единичной длины - НВЕД). Преобразование c jk имеет вид:

~			c j				n	~
c j					, тогда Lk (x) c jk x j .
			n
			c2j				j 1
			j 1

2-й вариант нормировки «сжимает/растягивает» оси Lk так, чтобы максимальный размах каждой ЦФ не превышал 1. Тогда

	~		c j
	c j
			Lmax

2.4. Метод линейной (аддитивной) свертки ЦФ

Скаляризованный критерий примет вид:

				K		n	K	n
L(		,		) k Lk (		) ( k c jk )x j		c j (		)x j .
			x		x
				k 1		j 1	k 1	j 1

K

k - весовые коэффициенты ЦФ. Обычно k 1.

k 1

Если частные ЦФ неоднородны, то их можно нормировать (как в п.2).

17

2.5. Метод «идеальной точки»

Векторная ЦФ L рассматривается как точка в m-мерном пространстве ЦФ.

Если известны предельные значения изменения каждой ЦФ и желаемое (идеальное)

значение каждой из них, то идеальной точкой L И будет одна из вершин m-мерного гиперкуба. Тогда задача оптимизации заключается в минимизации расстояния до идеальной точки.

Скалярная свѐртка векторной ЦФ примет вид:

K

)

(Lk (

) LИk )2 ,

откуда

opt arg min L(

) .

L(

x

x

x

x

k 1

x

2.6. Метод последовательных уступок

На 1-м этапе, как и в методе главного критерия, частные критерии (показатели) ранжируются по важности, например:

L1 (x) L2 (x) LK (x)

На 2-м этапе для самого важного критерия решается задача оптимизации:

xopt_1 arg max L1 (x)

x

На 3-м этапе для самого важного критерия (здесь L1 (x) ) назначается уступка – величина L1 , на которую допустимо его ухудшение, в результате чего формируется ограничение: L1 (x) L1_ opt L1 , которое используется на следующем этапе (аналогичном 2-

му).

На 4-м этапе для следующего по важности критерия решается задача оптимизации:

xopt _ 2 arg max L2 (x) при ограничении L1 (x) L1_ opt L1 .

x

На 5-ом этапе для L2 (x) назначается уступка L2 и формируется очередное ограничение: L2 (x) L2 _ opt L2 .

На 6-м этапе для следующего по важности критерия решается задача оптимизации:

xopt _ 3 arg max L3 (x) при ограничениях

x

L1 (x) L1_ opt L1 L2 (x) L2 _ opt L2

Ит.д. до последнего по важности критерия LK (x) .

2.7.Метод, основанный на Парето-оптимальности

Определение. Альтернатива x1 доминирует над альтернативой x 2 , если по всем критериям x1 не уступает альтернативе x 2 , а хотя бы по одному из них лучше.

Суть метода заключается в построении проекции ОДР, расположенной в координатах x1 xn , на пространство критериев L1 LK . С учѐтом доминирования из множества

альтернатив отбрасываются все недоминируемые. Оставшееся множество недоминируемых альтернатив называется Парето-оптимальным или множеством Парето (МП).

МП состоит из множества таких альтернатив, что любая другая альтернатива будет хуже хотя бы по одному критерию.

МП обычно имеет характер границы, поэтому его иногда называют границей Парето. После того, как выявлено МП, далее единственное оптимальное решение следует

выбирать из множества Парето. Для этого можно привлечь один из приведенных выше методов, а МП рассматривать как ограничение.

Пример. Пусть n 2; m 4; K 2 . Т.е. решается ЗЛП с двумя критериями:

18

2

2

c jk x j max ,

Lk (x)

Lk (x) c jk x j

max ,

k

1,2

j 1

x

j 1

x

2

k 1,2

aij x j

bi , i

~

1,4

2

~

Lk

bi ,

i 1,4

j 1

aik

k 1

x j 0 ,

j 1,2

Lk 0 ,

k 1,2

x2

L1

L2

Граница

L2

Парето

ОДР

ОДР

L1

x1

▲

Пример. Необходимо выбрать один из 10 вариантов поставки партии сырья. Каждый вариант имеет свои значения таких важных показателей, как срок поставки T и стоимость партии S. Оба показателя необходимо минимизировать. Данные по вариантам приведены в таблице:

Показатель	1	2	3	4	5	6	7	8	9	10
T	13	5	11	2	10	16	12	15	9	5
S	2	9	4	8	7	2	5	5	11	11

S

10

9

2

4

5

7 8

3

1 6

T

Здесь каждая доминирующая точка исключает из рассмотрения все другие точки (доминируемые), которые попали в еѐ сектор доминирования (синие пунктиры).

Оставшиеся доминирующие черные и красные точки образуют множество (границу) Парето.

Дальнейший отбор можно, например, выполнить с применением критерия Вальда, предварительно пронормировав значения показателей, т.е. приведя к интервалу [0;1], где 0 соответствует минимальному значению в строке, а 1 – максимальному в строке:

Показатель	1	3	4	5
Lk
T	13	11	2	10
S	2	4	8	7

19

Показатель	1	3	4	5	max
Lk					j
T	1	0.82	0	0.73	1
S	0	0.33	1	0.83	1

По критерию Вальда min max Lkj , т.е оптимальными можно считать варианты 1 и 4. Они

k j

наилучшие из наихудших.

▲

Особенности скаляризации векторных критериев.

1.Для упрощения задачи векторной оптимизации могут применяться и другие варианты свѐрток, например:

o мультипликативные;

o с нелинейными (штрафными) весами;

o комбинации приведенных вариантов свѐрток.

2.Все варианты свѐрток можно разделить на 2 группы:

oсводящие векторную оптимизацию к скалярной (например, приведенные выше варианты 1, 3, 4, 5);

o упрощающие векторную оптимизацию путѐм уменьшения количества альтернатив (например, варианты 2, 6).

3. К недостаткам свѐртки можно отнести следующие:

o сложности интерпретации оптимального решения при неоднородных ЦФ (представленных разными единицами измерения – баллы, рубли, время, …);

oсложность свѐртки структурно разных ЦФ, например, линейных и нелинейных.

4.В тех случаях, когда в процедурах свѐртки участвуют эксперты, появляются дополнительные проблемы, такие как:

oэксперты могут стать дополнительным источником неопределѐнности;

o возникает дополнительные задачи подбора экспертов задача, оценки их компетентности и других характеристик.

3. Модели управления запасами

3.1. Задача управления запасами

Опр. Запасом называют любой материальный или другой ресурс, хранящийся на предприятии для удовлетворения будущих потребностей.

Сферы применения:

Производство.

Склады.

Торговля.

Цепочки поставок.

Причины создания запасов (приводящие к желанию увеличить запасы):

1.Дискретный характер поставок при непрерывном потреблении.

2.Случайный и/или сезонный характер спроса, времени и объема поставок.

3.Упущенная прибыль при отсутствии запасов.

Причины отказа от запасов (приводящие к желанию уменьшить запасы):

1.Плата за хранение.

2.Физический износ (порча, ограниченный срок хранения).

3.Моральный износ (старение модели/типа материала). Значимость запасов:

Стоимостная.

Технологическая.

20