
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
- •Процесс ортогонализации.
- •Ортогональное дополнение. Ортогональная проекция и составляющая.
- •Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
- •. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.
- •Псевдорешения. Метод наименьших квадратов.
- •Нормальное решение
- •Нормальное псевдорешение.
- •Унитарное пространство.
- •Билинейные функции, квадратичные формы.
- •Билинейные формы. Квадратичные формы.
- •Полуторалинейные формы. Эрмитовы формы.
- •Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса.
- •Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
- •Метод выделения квадратов (Лагранжа).
- •Приведение квадратичных форм к нормальному виду элементарными преобразованиями
- •Закон инерции квадратичных форм.
- •Теорема Якоби
- •Критерий Сильвестра.
- •Квадрики.
- •Алгебраическая поверхность
- •Уравнение квадрики.
- •Изменение квадрики при аффинном преобразовании
- •Приведение уравнения квадрики к простейшему виду
- •Аффинная классификация кривых второго порядка.
- •Аффинная классификация поверхностей второго порядка
- •Линейный оператор
- •Линейный оператор. Матрица линейного оператора.
- •Примеры линейных операторов.
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора при изменении базиса.
- •Алгебра линейных операторов.
- •Простейший вид матрицы линейного оператора.
- •Эквивалентность матриц
- •Ранг, дефект линейного оператора.
- •Линейное преобразование
- •Линейное преобразование. Его матрица
- •Изменение матрицы линейного преобразования при изменении базиса.
- •Алгебра линейных преобразований.
- •Инвариантные пространства
- •Собственные векторы и собственные числа. Характеристическое уравнение.
- •Коэффициенты характеристического уравнения. След матрицы.
- •Диагонализируемые преобразования
- •Теорема Шура
- •Сопряженные преобразования.
- •Линейное преобразование и билинейные функции
- •Сопряженное преобразование. Свойства.
- •Нормальное преобразование и его свойства.
- •Ортогональные преобразования
- •Самосопряженное преобразование.
- •Полярное разложение
- •Приведение квадратичных форм
- •Приведение квадратичных форм к главным осям.
- •Приведение пары квадратичных форм
- •Первый способ
- •Пучок матриц
- •Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
- •Ортогональная классификация кривых второго порядка
- •Ортогональная классификация поверхностей второго порядка.
- •Аннулирующий многочлен
- •Аннулирующий многочлен вектора.
- •Аннулирующий многочлен подпространства
- •Функции от матриц
- •Вычисление линейных рекуррентных последовательностей
Процесс ортогонализации.
Пусть
![]() линейно не зависимая система векторов.
Следующий процесс позволяет строить
эквивалентную ей ортогональную систему
векторов:
линейно не зависимая система векторов.
Следующий процесс позволяет строить
эквивалентную ей ортогональную систему
векторов:
Положим
![]() ,
, ,
…,
,
…, …
. Процесс не может быть продолжен только
в случае, когда
…
. Процесс не может быть продолжен только
в случае, когда![]() .
Но тогда
.
Но тогда ,
и, значит,
,
и, значит,![]() ,
что противоречит линейной независимости
исходной системы векторов.
,
что противоречит линейной независимости
исходной системы векторов.
Ортогональность
построенной системы проверяется
непосредственно. Допустим, ортогональность
системы векторов
![]() установлена. Покажем, что вектор
установлена. Покажем, что вектор![]() ортогонален всем векторам, построенным
ранее него. Действительно,
ортогонален всем векторам, построенным
ранее него. Действительно, ,
гдеk=1,2,…i-1.
В силу ортогональности системы векторов
,
гдеk=1,2,…i-1.
В силу ортогональности системы векторов
![]() в сумме из правой части равенства только
одно не нулевое слагаемое, получаемое
приj=k.
Следовательно,
в сумме из правой части равенства только
одно не нулевое слагаемое, получаемое
приj=k.
Следовательно,
 .
.
Следствие 2.1 В любом подпространстве конечномерного евклидова пространства имеется ортогональный базис.
Доказательство. Возьмем базис подпространства и применим к нему процесс ортогонализации. В результате будет построена ортогональная система векторов (а, значит, и линейно независимая) из этого подпространства. Поскольку количество векторов в построенной системе совпадает с размерностью подпространства, то, следовательно, построенная ортогональная система векторов является базисом подпространства.
Следствие 2.2. Любую ортогональную систему векторов можно дополнить до ортогонального базиса всего пространства.
Доказательство.
Пусть
![]() - ортогональная система векторов.
Дополним ее до базиса всего пространства
векторами
- ортогональная система векторов.
Дополним ее до базиса всего пространства
векторами
![]() и к полученной системе
и к полученной системе
![]() применим процесс ортогонализации. В
результате будет построен ортогональный
базис
применим процесс ортогонализации. В
результате будет построен ортогональный
базис
![]() всего пространства. Поскольку первые
k
векторов были ортогональны, то в процессе
ортогонализации они не изменились, т.е.
всего пространства. Поскольку первые
k
векторов были ортогональны, то в процессе
ортогонализации они не изменились, т.е.
![]() ,…,
,…,![]() .
Таким образом, векторы
.
Таким образом, векторы![]() дополняют ортогональную систему
дополняют ортогональную систему![]() до ортогонального базиса всего
пространства.
до ортогонального базиса всего
пространства.
Следствие 2.3.
Пусть![]() - базис пространства, а
- базис пространства, а![]() - ортогональный базис пространства,
полученный из базиса
- ортогональный базис пространства,
полученный из базиса![]() процессом ортогонализации. Тогда матрица
перехода от одного базиса к другому
является треугольной, и на ее главной
диагонали стоят 1.
процессом ортогонализации. Тогда матрица
перехода от одного базиса к другому
является треугольной, и на ее главной
диагонали стоят 1.
Доказательство.
Согласно процессу ортогонализации
имеем
![]() ,
, ,
…,
,
…,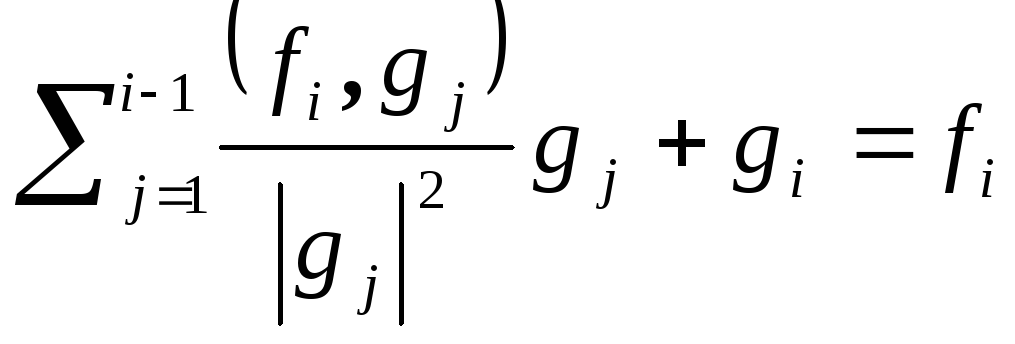 …,
а, значит, матрица переходаP
(ее столбцы –
координаты базисных векторов) равна
…,
а, значит, матрица переходаP
(ее столбцы –
координаты базисных векторов) равна
 .
.
Ортогональное дополнение. Ортогональная проекция и составляющая.
Пусть V – евклидово пространство со скалярным произведением (x,y), W – подпространство V.
Множество
всех векторов x,
ортогональных всем векторам из W,
которое обозначим
![]() ,
называется ортогональным дополнением
к подпространствуW.
Опишем свойства ортогонального
дополнения.
,
называется ортогональным дополнением
к подпространствуW.
Опишем свойства ортогонального
дополнения.
Свойство 2.8.![]() - линейное подпространствоV.
- линейное подпространствоV.
Доказательство.
Пусть
![]() ,
тогда
,
тогда![]() справедливы равенства
справедливы равенства![]() и
и![]() .
Из этих равенств выводим равенства
.
Из этих равенств выводим равенства![]() и
и![]() ,
то есть
,
то есть![]() .
Тем самым свойство доказано.
.
Тем самым свойство доказано.
Свойство 2.9![]() .
.
Доказательство.
Построим ортогональный базис
![]() подпространстваW
и дополним его
до ортогонального базиса
подпространстваW
и дополним его
до ортогонального базиса
![]() всего пространстваV.
Векторы
всего пространстваV.
Векторы
![]() ортогональны векторам
ортогональны векторам![]() ,
а, значит и любому вектору изW.
Следовательно, векторы
,
а, значит и любому вектору изW.
Следовательно, векторы
![]() принадлежат ортогональному дополнению
кW.
Разложим произвольный вектор x
по базису
принадлежат ортогональному дополнению
кW.
Разложим произвольный вектор x
по базису
![]() и положим
и положим![]() ,
,![]() .
Посколькуx=y+z
и
.
Посколькуx=y+z
и
![]() ,
,![]() ,
то установлено равенство
,
то установлено равенство![]() .
.
Покажем,
что сумма прямая. Пусть
![]() ,
тогда (x,x)=0
как скалярное произведение вектора из
W
на вектор из ортогонального дополнения
к W.
Единственный вектор нулевой длины равен
0, и, значит, пересечение содержит только
нулевой вектор и сумма прямая.
,
тогда (x,x)=0
как скалярное произведение вектора из
W
на вектор из ортогонального дополнения
к W.
Единственный вектор нулевой длины равен
0, и, значит, пересечение содержит только
нулевой вектор и сумма прямая.
Следствие 2.4![]() .
.
Доказательство вытекает из свойства прямой суммы подпространств.
Любой
вектор x
пространства
V
можно представить в виде суммы вектора
y
из подпространства W
и вектора z
из
![]() ,
причем векторыy
и z
определяются единственным образом.
Вектор y
называется ортогональной проекцией x
на W
и обозначается
,
причем векторыy
и z
определяются единственным образом.
Вектор y
называется ортогональной проекцией x
на W
и обозначается
![]() ,
а векторz
– ортогональной составляющей вектора
x
и обозначается
,
а векторz
– ортогональной составляющей вектора
x
и обозначается
![]() .
О способах построения ортогональной
проекции и ортогональной составляющей
будет разговор в п.2.6.
.
О способах построения ортогональной
проекции и ортогональной составляющей
будет разговор в п.2.6.
Свойство 2.10.![]() .
.
Доказательство.
Применив Следствие 2 .4, получим
![]() .
Пустьx
– произвольный вектор из W.
Поскольку для произвольного вектора
.
Пустьx
– произвольный вектор из W.
Поскольку для произвольного вектора
![]() скалярное произведение (x,y)=0,
то
скалярное произведение (x,y)=0,
то
![]() .
Тем самым показано включение
.
Тем самым показано включение![]() ,
из которого, в силу совпадения размерностей,
выводим равенство
,
из которого, в силу совпадения размерностей,
выводим равенство![]() .
.
Пусть
![]() базисW.
Вектор z
принадлежит ортогональному дополнению
к W
тогда и только тогда, когда
базисW.
Вектор z
принадлежит ортогональному дополнению
к W
тогда и только тогда, когда
![]() ,
,![]() ,
…,
,
…,![]() .
Пусть
.
Пусть![]() базис пространстваV.
В координатах, эти равенства превращаются
в систему линейных уравнений
базис пространстваV.
В координатах, эти равенства превращаются
в систему линейных уравнений
 .
Взяв в качествеW
ортогональное дополнение к нему, получим
следующее утверждение.
.
Взяв в качествеW
ортогональное дополнение к нему, получим
следующее утверждение.
Свойство 2.11. Любое подпространство может быть задано системой линейных однородных уравнений.
В
случае, если базис
![]() ортонормированный, коэффициентами при
неизвестных в системе линейных уравнений
являются координаты базисных векторов
ортогонального дополнения.
ортонормированный, коэффициентами при
неизвестных в системе линейных уравнений
являются координаты базисных векторов
ортогонального дополнения.
